Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Максимальный балл – 100. Проведен анализ, получено решение с правильным ответом.Содержание книги
Поиск на нашем сайте
II (муниципальный) этап Физика 10 класс Решения. Критерии проверки Общее время выполнения работы – 4 часа. Задание 1. Небольшая лампочка освещает вертикальную стену. Проходящий вдоль стены хулиган швырнул в лампочку камень под углом 45° к горизонту и попал в неё. Найдите закон движения h(t) тени от камня по стене, считая, что лампочка и точка броска находятся на одной и той же высоте h = 0, а в момент броска хулиган находился на расстоянии L от лампочки.
Решение
Пусть Тогда
Из рисунка 1 видно, что Пусть Подставив
Умножим и разделим на
Учтем (1) и (2)
Таким образом, тень от камня по стене будет двигаться с постоянной скоростью. Так как дальность полета
Максимальный балл – 100. Проведен анализ, получено решение с правильным ответом. 80 баллов. Идея решения верна. Ответ получен неверно из-за ошибок в выкладках. 50 баллов. Написаны исходные кинематические формулы. До 30 баллов, по усмотрению проверяющего, за разумные идеи или формулы.
Задание 2 Груз массы m1 находится на столе, который движется горизонтально с ускорением а (рис. 2). К грузу присоединена нить, перекинутая через блок. К другому концу нити подвешен второй груз массы m2. Найти силу натяжения нити Τ, если коэффициент трения груза массы m1 о стол равен μ.
Решение Пусть угол между вертикалью и нитью, прикрепленной к грузу массы Горизонтальная составляющая ускорения груза массы
а вертикальная
Из второго закона Ньютона в проекции на горизонтальную и вертикальную оси (ось y вниз):
Два последних уравнения при исключении угла дают следующее уравнение:
При наличии проскальзывания
Без проскальзывания
Максимальный балл – 100. Проведен анализ и получено правильное решение. Баллов. Идея решения верна, но сделаны математические ошибки. 60 баллов. Правильно написаны исходные формулы. До 30 баллов, по усмотрению проверяющего, за разумные идеи или формулы. Задание 3 В двух калориметрах налито по 200 г воды – в одном температура t = +300 С, в другом t = + 400 С. Из «горячего» калориметра зачерпывают 50 г воды, переливают в «холодный» и перемешивают. Затем из «холодного» калориметра переливают 50 г воды в «горячий» и снова перемешивают. Сколько раз нужно перелить такую же порцию воды туда-обратно, чтобы разность температур воды в калориметрах стала меньше 1 °С? Потерями тепла в процессе переливаний и теплоёмкостью калориметров пренебречь Решение Обозначим исходные температуры горячей воды –
Здесь т — исходная масса воды, находившейся в каждом из калориметров, С — удельная теплоёмкость воды. Из этого уравнения находим:
где введено обозначение Далее найдём, какая температура
Отсюда:
Тогда после одного переливания туда-обратно разность температур в калориметрах составит
Ясно, что для того, чтобы получить разность температур в калориметрах
Таким образом, понятно, что при каждом переливании туда-обратно разность температур изменяется в В нашем случае
С учётом этого окончательно имеем: разность температур после первого переливания туда-обратно будет равна 10 °С · 0,6 = 6 °С, после второго переливания 10 °С · 0,62 = 3,6 °С, после третьего переливания 10 °С · 0,63 ≈ 2,2 °С, после четвёртого 10 °С · 0,64 ≈ 1,3 °С, после пятого 10 °С · 0,65 ≈ 0,8 °С. Значит, для того, чтобы разность температур воды в калориметрах стала меньше 1 °С, достаточно сделать пять переливаний.
Максимальный балл – 80. Проведен анализ, получено решение с правильным ответом. 50 – 60 баллов. Идея решения верна. Ответ получен неверно из-за ошибок в выкладках. Задание 4 В вакуумном диоде, анод и катод которого — параллельные пластины, зависимость тока I от напряжения U дается формулой I = c·U3/2, где c — некоторая постоянная. Во сколько раз увеличится сила давления на анод, возникающая из-за ударов электронов о его поверхность, если напряжение на диоде увеличить в два раза? Начальной скоростью электронов, вылетающих из катода, пренебречь.
Решение Рассмотрим небольшой интервал времени
и сообщат ему импульс, равный
Скорость v электрона у анода можно найти из закона сохранения энергии:
Согласно второму закону Ньютона
тогда
отсюда с учетом связи
Таким образом, отношение сил
Задание 5 Автомобиль движется со скоростью
Решение
.
При отражении звука угол падения равен углу отражения, т. е. задачу можно рассматривать аналогично оптической задаче на отражение света в плоском зеркале (рис.3). В момент подачи сигнала изображение источника звука будет расположено симметрично относительно стены по другую сторону от нее на расстоянии
Искомое расстояние
отсюда
Решение со знаком «-» не имеет смысла. Окончательно имеем
II (муниципальный) этап Физика 10 класс Решения. Критерии проверки Общее время выполнения работы – 4 часа. Задание 1. Небольшая лампочка освещает вертикальную стену. Проходящий вдоль стены хулиган швырнул в лампочку камень под углом 45° к горизонту и попал в неё. Найдите закон движения h(t) тени от камня по стене, считая, что лампочка и точка броска находятся на одной и той же высоте h = 0, а в момент броска хулиган находился на расстоянии L от лампочки.
Решение
Пусть Тогда
Из рисунка 1 видно, что Пусть Подставив
Умножим и разделим на
Учтем (1) и (2)
Таким образом, тень от камня по стене будет двигаться с постоянной скоростью. Так как дальность полета
Максимальный балл – 100. Проведен анализ, получено решение с правильным ответом. 80 баллов. Идея решения верна. Ответ получен неверно из-за ошибок в выкладках. 50 баллов. Написаны исходные кинематические формулы.
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-08-25; просмотров: 194; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.118.214 (0.007 с.) |


 скорость камня в момент броска. Так как угол
скорость камня в момент броска. Так как угол  , то
, то 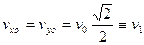


 время полета камня, тогда
время полета камня, тогда  (1) и
(1) и  (2)
(2)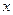 и
и  в выражение для
в выражение для  , получим
, получим
 и учтем, что
и учтем, что 
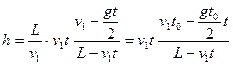
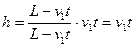
 , то окончательно получим:
, то окончательно получим:

 равен
равен  , а ускорение груза массы
, а ускорение груза массы  относительно стола равно
относительно стола равно  . Тогда ускорение груза массы
. Тогда ускорение груза массы  .
.



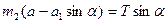

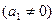



 и холодной –
и холодной – 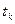 . Рассчитаем, какая температура
. Рассчитаем, какая температура  установится в «холодном» калориметре после переливания в него горячей воды массой
установится в «холодном» калориметре после переливания в него горячей воды массой  . Из уравнения теплового баланса имеем:
. Из уравнения теплового баланса имеем:


 установится в «горячем» калориметре после переливания в него массы воды
установится в «горячем» калориметре после переливания в него массы воды 


 после второго переливания туда-обратно, нужно в последней формуле заменить
после второго переливания туда-обратно, нужно в последней формуле заменить 
 раз.
раз. = 10 °С,
= 10 °С,  = 0,25 и
= 0,25 и 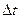 . За этовремя к аноду подлетят
. За этовремя к аноду подлетят электронов ( где е — заряд электрона)
электронов ( где е — заряд электрона) .
.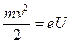

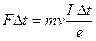
 получаем
получаем
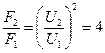
 мимо длинной стены, удаляясь от нее под углом
мимо длинной стены, удаляясь от нее под углом 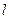 , шофер подает короткий звуковой сигнал. Какое расстояние пройдет автомобиль до момента, когда шофер услышит эхо? Скорость звука в воздухе равна c.
, шофер подает короткий звуковой сигнал. Какое расстояние пройдет автомобиль до момента, когда шофер услышит эхо? Скорость звука в воздухе равна c.
 время, через которое шофер услышит эхо, то за это время автомобиль пройдет путь
время, через которое шофер услышит эхо, то за это время автомобиль пройдет путь  , а звук – путь ct. Из геометрических построений получаем (рис.3)
, а звук – путь ct. Из геометрических построений получаем (рис.3)
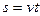 и заменим
и заменим  , тогда
, тогда