
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Одноканальной СМО с отказамиСодержание книги
Поиск на нашем сайте
Окончание табл. 8
Пример 6. Пусть на телефонную линию филиала банка производительностью Так как математической моделью телефонной линии является одноканальная CMО с отказами, характеризующаяся параметрами: интенсивностью входящего потока
т. е. в установившемся режиме из каждых 100 заявок в среднем 53 получают отказ. Определим предельное значение относительной Q и абсолютной А пропускной способности СМО:
Из расчета следует, что случайный характер поступления телефонных вызовов и случайный характер длительности разговоров порождают ситуацию, что абсолютная пропускная способность Среднее время обслуживания Среднее время простоя канала Вероятность того, что канал свободен,
Вероятность того, что канал занят,
Таким образом, вероятность того, что канал занят, больше вероятности того, что канал свободен, и этого следовало ожидать, так как интенсивность входящего потока 2. Многоканальная СМО с отказами (задача Эрланга). Имеется n каналов, на которые поступает поток заявок с интенсивностью l. Поток обслуживания имеет интенсивность m. Предельные характеристики эффективности функционирования многоканальной СМО с отказами приведены в табл. 9. Пример 7. Пункт по приему техники работает в режиме отказа с двумя бригадами. Интенсивность потока заявок Таблица 9 Предельные характеристики функционирования Многоканальной СМО с отказами
Рассчитываем интенсивность потока обслуживания
Коэффициент использования
Отсюда:
3. Одноканальная система с неограниченной очередью В качестве показателей эффективности СМО с ожиданием, кроме уже известных показателей, рассматривают также следующие: L сист– среднее число заявок в системе, Т сист – среднее время пребывания заявки в системе, L оч – среднее число заявок в очереди (длина очереди), T оч–среднее время пребывания заявки в очереди. Имеется одноканальная СМО с очередью, на которую не наложены никакие ограничения (ни по длине очереди, ни по времени ожидания). Поток заявок, поступающих в СМО, имеет интенсивность l, а поток обслуживания – интенсивность m. Предельные характеристики эффективности функционирования одноканальной СМО с ожиданием приведены в табл. 10. Таблица 10
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 269; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.92.5 (0.008 с.) |









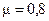 вызовов/мин и простейшим потоком обслуживания поступает простейший поток вызовов клиентов с интенсивностью
вызовов/мин и простейшим потоком обслуживания поступает простейший поток вызовов клиентов с интенсивностью  вызовов/мин. Определить предельные значения относительной пропускной способности Q,абсолютной пропускной способности А и вероятность отказа р отктелефонной линии. Определить также среднее время обслуживания одного вызова, среднее время простоя канала и вероятность того, чтоканал свободен или занят.
вызовов/мин. Определить предельные значения относительной пропускной способности Q,абсолютной пропускной способности А и вероятность отказа р отктелефонной линии. Определить также среднее время обслуживания одного вызова, среднее время простоя канала и вероятность того, чтоканал свободен или занят. или
или  ,
, ,
, .
.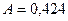 разговора/мин почти в два раза меньше производительности телефонной линии
разговора/мин почти в два раза меньше производительности телефонной линии  мин.
мин. мин.
мин. .
. .
. заявки в день, среднее время обслуживания заявки
заявки в день, среднее время обслуживания заявки  . Определить вероятность того, что оба канала свободны, один канал занят, оба канала заняты, вероятность отказа, относительную и абсолютную пропускные способности, среднее число занятых бригад.
. Определить вероятность того, что оба канала свободны, один канал занят, оба канала заняты, вероятность отказа, относительную и абсолютную пропускные способности, среднее число занятых бригад.
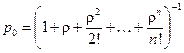

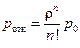

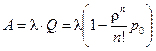

 .
. – количество заявок, поступающих за время выполнения одной заявки. Далее:
– количество заявок, поступающих за время выполнения одной заявки. Далее: ,
, ,
,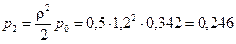 .
. ,
, ,
, ,
,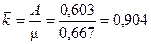 .
.


