Классы компьютеров. Виды настольных и мобильных ПК? Их особенности.

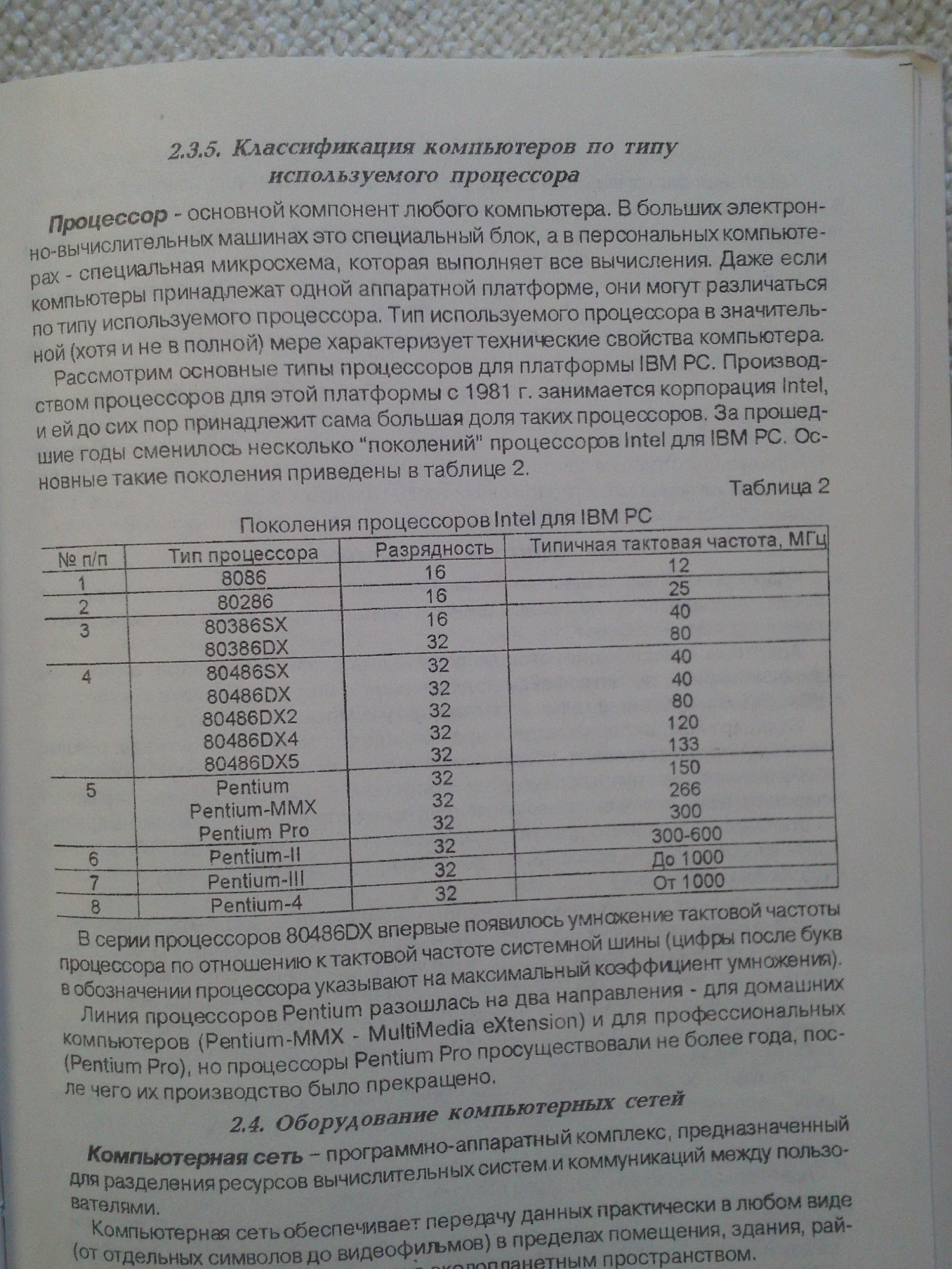
Существуют различные классификации компьютерной техники:

	ü по этапам развития (по поколениям);
	ü по архитектуре;
	ü по производительности;
	ü по условиям эксплуатации;
	ü по количеству процессоров;
	ü по потребительским свойствам и т.д.

Четких границ между классами компьютеров не существует. По мере совершенствования структур и технологии производства, появляются новые классы компьютеров, границы существующих классов существенно изменяются.

Персональный компьютер (ПК) - это вид компьютера, спроектированный для использования отдельным человеком, отсюда и такое название. ПК изначально были известны как микрокомпьютеры.

Сервер. Вид компьютера, оптимизированный для того, чтобы предоставлять другим компьютерам сервисы через сеть. У компьютеров этого вида обычно очень мощные процессоры, много памяти и объёмные жесткие диски.

Следующий вид: мейнфрейм. На заре компьютерной эпохи это были огромные машины, занимающие комнату, две, а то и целый этаж. Постепенно размер компьютеров уменьшался, в то время как мощность росла. Термин "мейнфрейм" постепенно вышел из употребления, вместо него используется "сервер предприятия". Однако его всё ещё можно услышать, как правило, в больших компаниях, чтобы описать огромные машины, обрабатывающие миллионы операций каждый день.

Суперкомпьютер. Этот вид компьютера обычно стоит сотни тысяч или даже миллионы долларов. Невзирая на то, что некоторые суперкомпьютеры - это отдельные компьютерные системы, большинство из них включает множество высокопроизводительных компьютеров, работающих параллельно как единая система.

 

 

18. Применение Булевой алгебры?

 

Булева алгебра (алгебра логики) - это математический аппарат, с помощью которого записывают, вычисляют, упрощают и преобразовывают логические высказывания.

Создателем алгебры логики является живший в ХIХ веке английский математик Джордж Буль, в честь которого эта алгебра названа булевой алгеброй высказываний.

Булева алгебра может применяться в компьютерной технике. Здесь интерпретация заключается в том, что значок 0 означает одно напряжение между какими-нибудь контактами какой-нибудь схемы (скажем, 0 вольт), а значок 1 - другое (скажем, +5 вольт).

Второй вариант применения булевой алгебры - логические рассуждения. Здесь два объекта интерпретируются как истина (true) и ложь (false). Далее мы будем называть символы true и false булевыми величинами, а переменные, которые их обозначают - булевыми переменными.

Есть одна тонкость, которую люди, впервые столкнувшиеся с математической логикой, понимают с трудом. Поэтому придется сделать пространное отступление.

Что называть истиной, а что - ложью,- это вопрос, как говорится, "тонкий". Есть разные критерии истины, о которых можно долго говорить. Математическая логика подобных разговоров избегает, как говорят "абстрагируется" от них. Предполагается, что кто-то каким-то образом выяснил, что некое утверждение истинно (true), а другое - ложно (false). Дальше уже можно применять булеву алгебру для различных операций с этими true и false. Результат будет получен, опять же, в виде true и false.

В булевой алгебре рассматриваются только те высказывания, для которых истинность может принимать два значения: либо истина (true), либо ложь (false). Другие значения - нельзя. Оба значения сразу - нельзя. Ни одного значения вообще - тоже нельзя. Подобные высказывания называются булевыми высказываниями. Любые другие тексты в булевой алгебре не рассматриваются.

Булево высказывание - это такое высказывание, для которого рассматриваются только два значения истинности: true и false.

 

При создании первых вычислительных машин было выяснено, что удобнее всего производить все вычислительные операции в двоичном коде. Для реализации каких – либо операций (сложение, умножение) в двоичном коде необходимо гораздо меньше устройств и элементов, чем в десятичном коде, т. к. в двоичной системе используется только две цифры – 0 и 1.

За единицу информации принят 1 бит (да или нет, 0 или 1)

В алгебре логики за «нуль» принимается ложное высказывание, отсутствие какого-либо действия или сигнала, выключенный элемент или устройство.

За «единицу» принимается истинное высказывание, присутствие какого- либо действия, наличие сигнала, включение устройства.

Логическая переменная – переменная, принимающая только 2 значения: истинно – 1, ложно – 0.

Пусть Х1, Х2…Хn – логические переменные.

Если произвести с переменными Х1, Х2, - Хn какие – либо действия, в результате появится переменная У, которая зависит от состояния переменных Х1 – Хn.

У – это логическая функция переменных Х1, Х2, Хn.

Можно записать – У = f (х1..хn)

Логическая функция – это логическая зависимая переменная от одной или нескольких логических переменных. Логическая функция может принимать тоже только 2 значения: 1 – истинно, 0- ложно.

Раздел математики, занимающийся исследованием логических функций, называется алгеброй логики, или булевой алгеброй.

В вычислительных машинах, в устройствах управления сложными технологическими процессами используются устройства и элементы, которые имеют только два состояния – «включено» - «выключено». Это реле, транзисторы, работающие в ключевом режиме, тиристоры, электронные логические элементы.

Первые вычислительные машины появились перед второй мировой войной, они были исключительно на релейных элементах. Одна машина занимала несколько комнат.

Эти машины были ненадежны, громоздки, имели малое быстродействие. Затем появились машины на транзисторах, они были более надежны, меньшими габаритами. С появлением цифровых интегральных микросхем (БИС) появилась возможность создать современные компьютеры малых габаритов и большого быстродействия.

При разработке современных вычислительных устройств для управления сложными технологическими процессами вначале, используя логические функции булевой алгебры, создается математическая модель устройства, затем эта модель минимизируется, после этого создается устройство с использованием электронных элементов – микросхем.