
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Опишите особенности показателей качества проектируемых систем. Опишите классификации систем.Содержание книги
Поиск на нашем сайте
Чтобы определиться с выбором системы можно использовать комплексный показатель качества, в который будет входить сразу несколько выходных параметров системы. Этот метод применяется в случае наличия большого числа параметров. Существует 3 осн. подхода к формированию такого параметра: 1) аддитивный; 2) мультипликативный; 3) максиминный. Аддитивный критерий.
Аддитивный критерий объединяет все выходные параметры в одну целевую функцию, представляющую собой взвешенную сумму частных критериев. Весовые коэффициенты (ω) – получают методом экспертной оценки. Обычно сумма всех ω = 1. Параметры у должны быть представлены в безразмерной (относит.) форме. Главное, чтобы показатели стремились к одному экстремуму. F(x) → min. Если yj>Tj, то ωj<0. Мультипликативный критерий.
Главный недостаток этих критериев – субъективность выбора весовых коэффициентов. Максиминный критерий. В качестве целевой функции в этом критерии применяется выходной параметр наиболее неблагополучный с точки зрения с позиции выполнения неработоспособности. Для оценки выполнения условия работоспособности вводится понятие «запас работоспособности».
На все управляемые параметры «х» должны быть наложены ограничения. Классы проектируемой системы связи: 1) Информационные параметры (характеризуют способность системы передавать информацию в заданной полосе частот с определенной скоростью при наличии помех). 2) Технико-экономические (показывают как с помощью технических и экономических затрат можно достичь требуемых информационных параметров). 3) Конструктивно-технологические (хар-ют перспективность разработки системы, степень унификации оборудования и эстетические и эргономические показатели системы). 10.Опишите понятие и свойства множества «не худших» систем. Дайте классификацию и приведите примеры использования методов определения «не худших» систем. 1.Частный критерий оптимизации – среди выходных параметровв выбирают один в качестве целевой функции, а условия работоспособности остальных выходных параметров относятся к ограничениям задачи. Использование этого критерия приемлемо, если можно выделить один наиболее критичный выходной параметр.
2. Двухкритериальная задача. y1 и y2 – выходные параметры Т1 и Т2 – ограничения работоспособности y1<T1, y2<T2.
Алгоритм выбора «не худшей» системы: 1.выбираются конфигурации, имеющие оптимальные значения каждого из параметров; Точки – оптимальны по одному из параметров, уже относим к области Парето. 2.повторяется предыдущий шаг для каждого из прямоугольников. Cтроим следующий прямоугольник и тем самым уменьшается его область. Остальные точки «проигрывают». Их не рассматриваем.
Находим новую кривую Парето. Для формирования выбора системы можно использовать комплексный параметр с несколькими выходными параметрами системы. Методы для решения этих задач: 1). Аддитивный (объединяет все выходные параметры в одну целевую функцию, представляет собой взвешенную сумму частных критериев). 2). Мультипликативный (объединяет все выходные параметры в одну целевую функцию, представляет собой взвешенное произведение частных критериев; недостаток – субъективность выбора весовых коэффициентов). 3). Максимильный (в качестве целевой функции используют выходные параметры наиболее неблагоприятных с точки зрения работоспособности).
|
|||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 550; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.249.191 (0.006 с.) |

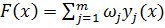 , ω – весовые коэффициенты; m – число выходных параметров.
, ω – весовые коэффициенты; m – число выходных параметров. , ω – весовые коэффициенты; m – число выходных параметров.
, ω – весовые коэффициенты; m – число выходных параметров. – запас работоспособности j-го параметра;
– запас работоспособности j-го параметра;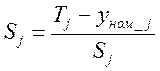 – показатель рассеяния j-го параметра;
– показатель рассеяния j-го параметра; ;
; ;
; Кривая АВ называется обл. Парето (область «не худших» систем, область компромисса).
Кривая АВ называется обл. Парето (область «не худших» систем, область компромисса). Нахождение «не худших» систем. Такой метод подходит для случая дискретного выбора. Существует несколько конфигураций, из которой нужно выбрать оптимальную. Точки – возможные конфигурации системы. Нужно выбрать «не худшие». Вариант конфигурации системы.
Нахождение «не худших» систем. Такой метод подходит для случая дискретного выбора. Существует несколько конфигураций, из которой нужно выбрать оптимальную. Точки – возможные конфигурации системы. Нужно выбрать «не худшие». Вариант конфигурации системы.


