
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Естественный и поляризованный свет.Содержание книги
Поиск на нашем сайте Естественный и поляризованный свет. Закон Малюса
Реальная световая волна, как отмечалось ранее (§2.10) слагается из множества цугов волн, испускаемых отдельными атомами. Плоскость колебаний вектора
Такая световая волна называется естественной. Световая волна, в которой направления колебаний вектора
Если колебания вектора Плоскополяризованную волну можно получить из естественной с помощью приборов, называемых поляризаторами. Эти приборы свободно пропускают колебания, параллельные плоскости, которую называют плоскостью поляризатора и полностью задерживают колебания, перпендикулярные к этой плоскости. Колебание с амплитудой
Если вращать поляризатор вокруг направления естественного луча, интенсивность прошедшего света не будет меняться, изменяется лишь ориентация плоскости колебаний вектора Пусть на поляризатор падает плоскополяризованный свет с амплитудой Через поляризатор пройдет составляющая колебания с амплитудой E=Emcosj, где j - угол между плоскостью колебаний вектора Следовательно, интенсивность света, прошедшего через поляризатор, определяется выражением
Выражение (2.18.1) называется законом Малюса.
Свет, в котором колебания одного направления преобладают над колебаниями других направлений, называется частично поляризованным. Такой свет можно рассматривать как смесь естественного и плоскополяризованного. Если пропустить частично поляризованный свет через поляризатор, то при вращении прибора интенсивность прошедшего света будет изменяться в пределах от jmax до jmin. Степенью поляризации называют выражение
Из (2.18.2) следует, что для плоскополяризованного света Р = 1, а для естественного Р = 0. При наложении друг на друга двух когерентных плоскополяризованных световых волн, плоскости колебаний вектора
В зависимости от направления вращения вектора Искусственное двойное лучепреломление. Эффект Керра Двойное лучепреломление может возникать в прозрачных изотропных телах, а также в кристаллах кубической системы под влиянием различных воздействий. В частности, это происходит при механических деформациях тел. Мерой возникающей оптической анизотропии может служить разность показателей преломления обыкновенного и необыкновенного лучей. Опытным путем установлено, что эта разность пропорциональна напряжению s в данной точке тела: no – ne = ks, (2.18.5) где k – коэффициент пропорциональности, зависящий от свойств вещества.
Пока стекло не деформировано, такая система не пропускает свет. Если стекло подвергнуть одностороннему сжатию, то в прошедших лучах будет наблюдаться картина, содержащая цветные полосы. Каждая полоса соответствует одинаково деформированным местам пластинки. Следовательно, по характеру и расположению полос можно судить о распределении напряжений внутри пластинки.
Ячейка Керра представляет собой герметичную кювету с жидкостью, в которую помещены пластины конденсатора. При подаче напряжения между пластинами создается однородное электрическое поле. Под действием электрического поля жидкость приобретает свойства одноосного кристалла с оптической осью, ориентированной вдоль поля. Разность показателей преломления no и пе пропорциональна квадрату напряженности поля: no – ne= кE2. (2.18.6) На пути l между обыкновенным и необыкновенным лучами возникает разность хода: D=(no – ne)l=кlE2, или разность фаз
Последнее выражение принято записывать в виде d =2pBlE2, (2.18.7) где В - характерная для вещества величина, называемая постоянной Керра, зависящая от температуры и длины волны света lо. Эффект Керра объясняется оптической анизотропией молекул жидкости, то есть различной поляризуемостью молекул по разным направлениям. Под действием поля молекулы поворачиваются так, что их дипольные моменты ориентируются вдоль поля. В результате жидкость становится анизотропной. Время в течение которого устанавливается или исчезает преимущественная ориентация молекул, составляет около 10-10 с. Таким образом, ячейка Керра, помещенная между скрещенными поляризаторами (рис. 2.18.10 ), может служить практически безинерционным световым затвором. В отсутствии напряжения затвор будет закрыт. При включении напряжения затвор пропускает значительную часть света, падающего на первый поляризатор. Такое устройство может быть использовано в оптических линиях связи для передачи информации, в частности, для осуществления амплитудной модуляции оптического излучения на очень высоких (до 1010 Гц) частотах. Дисперсия ЭМВ Дисперсией ЭМВ. называются явления, обусловленные зависимостью показателя преломления вещества от частоты (или длины) электромагнитной волны. Такая зависимость характеризуется функцией n = f(l0), (2.19.1) где l0 - длина волны в вакууме. Для всех прозрачных бесцветных веществ функция (2.19.1) в видимой части спектра описывается кривой, представленной на рисунке 2.19.1.
где a, b – постоянные, значения которых для каждого вещества определяются экспериментально. В этом случае дисперсия вещества зависит от l0 в соответствии с выражением
Рассеяние света возникает только в неоднородной среде. Световые волны, дифрагируя на неоднородностях среды, дают дифракционную картину, характеризующуюся довольно равномерным распределением интенсивности по всем направлениям. Такую дифракцию на мелких неоднородностях называют рассеянием света. Среды с явно выраженной оптической неоднородностью носят название мутных сред. К их числу относятся: 1) дымы, то есть взвеси мельчайших твердых частиц в газах; 2) туманы-взвеси в газах мельчайших частиц жидкости; 3) взвеси или суспензии, образованные плавающими в жидкости твердыми частичками; 4) эмульсии, то есть взвеси мельчайших капелек одной в другой, не растворяющей первую; 5) твердые тела вроде перламутра, опалов, молочных стекол. В результате рассеяния света в боковых направлениях интенсивность в направлении распространения убывает быстрее, чем в случае одного поглощения. Поэтому для мутного вещества в выражении (2.19.11), наряду с коэффициентом истинного поглощения c, должен стоять добавочный коэффициент c ', обусловленный рассеянием: J=J0e-(c+c')l. (2.19.12) Величина c' носит название коэффициента экстинкции. Если размеры неоднородностей малы по сравнению с длиной световой волны (не более 0,1 l), интенсивность рассеянного света J оказывается пропорциональной четвертой степени частоты и обратно пропорциональной четвертой степени длины волны:
Эта зависимость носит название закона Рэлея. Даже тщательно очищенные от посторонних примесей и загрязнений жидкости и газы, которые нельзя считать мутными средами, в некоторой степени рассеивают свет. Л.И.Мандельштам и М.Смолуховский установили, что причиной проявления оптических неоднородностей является в этом случае флуктуации плотности. Эти флуктуации вызваны беспорядочным движением молекул вещества; поэтому обусловленное ими рассеяние света называется молекулярным. Молекулярным рассеянием объясняется голубой цвет неба. Непрерывно возникающие в атмосфере, вследствие беспорядочного молекулярного движения, места сгущения и разрежения воздуха рассеивают солнечный свет. При этом согласно закону Рэлея голубые и синие лучи рассеиваются сильнее, чем желтые и красные, обуславливая голубой цвет неба. Когда Солнце находится низко над горизонтом, распространяющиеся непосредственно от него лучи проходят большую толщину рассеивающей среды, в результате чего они оказываются обогащенными большими длинами волн. По этой причине небо на заре окрашивается в красные тона.
Естественный и поляризованный свет. Закон Малюса
Реальная световая волна, как отмечалось ранее (§2.10) слагается из множества цугов волн, испускаемых отдельными атомами. Плоскость колебаний вектора
Такая световая волна называется естественной. Световая волна, в которой направления колебаний вектора
Если колебания вектора Плоскополяризованную волну можно получить из естественной с помощью приборов, называемых поляризаторами. Эти приборы свободно пропускают колебания, параллельные плоскости, которую называют плоскостью поляризатора и полностью задерживают колебания, перпендикулярные к этой плоскости. Колебание с амплитудой
Если вращать поляризатор вокруг направления естественного луча, интенсивность прошедшего света не будет меняться, изменяется лишь ориентация плоскости колебаний вектора Пусть на поляризатор падает плоскополяризованный свет с амплитудой Через поляризатор пройдет составляющая колебания с амплитудой E=Emcosj, где j - угол между плоскостью колебаний вектора Следовательно, интенсивность света, прошедшего через поляризатор, определяется выражением
Выражение (2.18.1) называется законом Малюса.
Свет, в котором колебания одного направления преобладают над колебаниями других направлений, называется частично поляризованным. Такой свет можно рассматривать как смесь естественного и плоскополяризованного. Если пропустить частично поляризованный свет через поляризатор, то при вращении прибора интенсивность прошедшего света будет изменяться в пределах от jmax до jmin. Степенью поляризации называют выражение
Из (2.18.2) следует, что для плоскополяризованного света Р = 1, а для естественного Р = 0. При наложении друг на друга двух когерентных плоскополяризованных световых волн, плоскости колебаний вектора
В зависимости от направления вращения вектора
|
||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 686; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

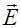 для каждого цуга ориентирована случайным образом. Поэтому в результирующей волне колебания вектора
для каждого цуга ориентирована случайным образом. Поэтому в результирующей волне колебания вектора 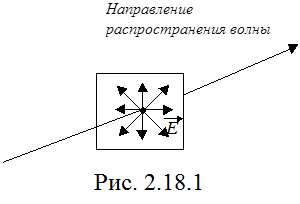
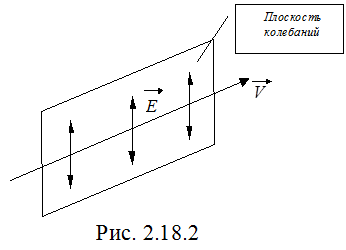
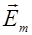 , совершающееся в плоскости, образующей угол j с плоскостью поляризатора, можно разложить на два колебания с амплитудами
, совершающееся в плоскости, образующей угол j с плоскостью поляризатора, можно разложить на два колебания с амплитудами 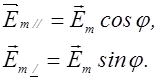
 Первое колебание пройдет через прибор, а второе будет задержано. Интенсивность прошедшей волны пропорциональна
Первое колебание пройдет через прибор, а второе будет задержано. Интенсивность прошедшей волны пропорциональна 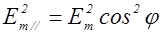 , то есть равна jmcos2j, где jm - интенсивность колебания с амплитудой
, то есть равна jmcos2j, где jm - интенсивность колебания с амплитудой 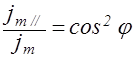 . В естественном свете все значения j равновероятны. Поэтому доля света, прошедшего через поляризатор, будет равна среднему значению cos2j, то есть 1/2.
. В естественном свете все значения j равновероятны. Поэтому доля света, прошедшего через поляризатор, будет равна среднему значению cos2j, то есть 1/2. j=jmcos2j. (2.18.1)
j=jmcos2j. (2.18.1)
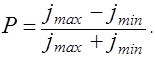 (2.18.2)
(2.18.2) Такой свет называется эллиптическим поляризованным. При разности фаз колебаний, кратной p, эллипс вырождается в прямую и получается плоскополяризованный свет. При разности фаз колебаний, равной нечетному числу
Такой свет называется эллиптическим поляризованным. При разности фаз колебаний, кратной p, эллипс вырождается в прямую и получается плоскополяризованный свет. При разности фаз колебаний, равной нечетному числу 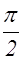 , и равенстве амплитуд эллипс превращается в окружность. В этом случае получается свет, поляризованный по кругу (§ 1.7).
, и равенстве амплитуд эллипс превращается в окружность. В этом случае получается свет, поляризованный по кругу (§ 1.7).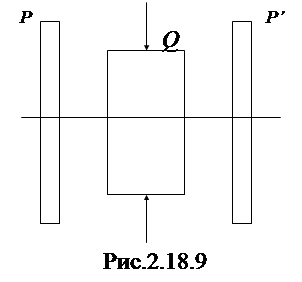 Поместим стеклянную пластинку Q между скрещенными поляризаторами P и P'
Поместим стеклянную пластинку Q между скрещенными поляризаторами P и P' 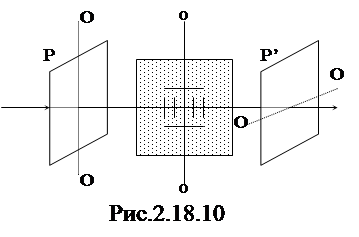 В 1875 году Керр обнаружил, что в жидкостях (и в аморфных твердых телах) под воздействием электрического поля возникает двойное лучепреломление. Это явление получило название эффекта Керра. На рис. 2.18.10 представлена схема установки для наблюдения эффекта Керра в жидкостях.
В 1875 году Керр обнаружил, что в жидкостях (и в аморфных твердых телах) под воздействием электрического поля возникает двойное лучепреломление. Это явление получило название эффекта Керра. На рис. 2.18.10 представлена схема установки для наблюдения эффекта Керра в жидкостях.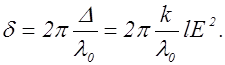
 Дисперсией вещества называется величина
Дисперсией вещества называется величина 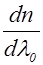 . Как видно на рис.2.19.1, с уменьшением l0 величина
. Как видно на рис.2.19.1, с уменьшением l0 величина 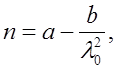 (2.19.2)
(2.19.2)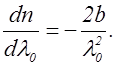 (2.19.3)
(2.19.3) Если вещество поглощает часть излучения, то в области поглощения и вблизи нее дисперсия обнаруживает аномалию (рис.2.19.2) в том, что короткие волны преломляются меньше, чем длинные. Такой ход зависимости n от l называется аномальной дисперсией.
Если вещество поглощает часть излучения, то в области поглощения и вблизи нее дисперсия обнаруживает аномалию (рис.2.19.2) в том, что короткие волны преломляются меньше, чем длинные. Такой ход зависимости n от l называется аномальной дисперсией.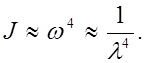 (2.19.13)
(2.19.13)


