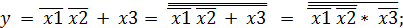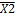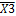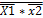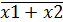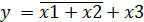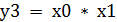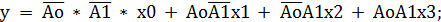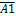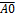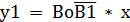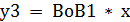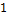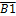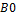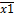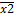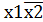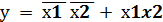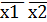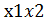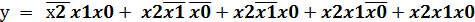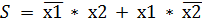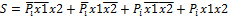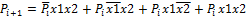Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Замечание: обычно требуется построение на универсальных элементах: «ИЛИ-НЕ», «И-НЕ».Содержание книги
Поиск на нашем сайте
Преобразуем полученную функцию:
3.4 Упрощение (минимизация) логических функций с помощью карт Вейча – Карно. Пример с 3-х аргументной функцией.
1.
2.
3. Карта Вейча – Карно В таблице приведены все возможные минтермы. Выделим «наши» минтермы: х3
х1 х2
х1
х1
4. Отмечаем в таблице клетки, соответствующие минтермам полученной функции.
1 1
1 1 1
Объединяем смежные клетки в контуре с числом клеток, равных 2n = 1;2; 4; 8….. Замечание: карту Карно можно склеить в кольцо. 5. Для каждого контура записываем слагаемые члены, которые повторяются во всем контуре. I – контур: х3 II – контур:
у = х3 +
Проверка: х1 = 0; х2 = 1; х3 = 0 __ __ у = 0 + 0 * 1 =0
х1 1 y
& 1 х2
х3
3.4.1 Карты Карно для 4-х аргументной функции.
Также по таблице истинности определяется минтермы. х1 u eG1sUEsFBgAAAAAEAAQA8wAAAPcFAAAAAA== " o:allowincell="f"/> Iый - контур
1 1 1 1 х2 1 1
1 1 х4
III-ий–контур 1 IIой - контур
х3
I контур: х2 * II контур: х3 * х4 III контур:
у = х2
Замечание: для 4-х такую карту можно склеивать не только с боков, но и свернуть снизу.
х1
1 1 х2
х4
1 1
I контур
3.4.2 Применение карт Карно для 5-ти аргументных функций. х1
х2 1 х4
х5
х3
х1
Построение логических схем в заданном базисе (т.е. на универсальных электронах).
(«И-НЕ», «ИЛИ-НЕ», «2И-НЕ»)
& 1 & 1
&
Пример: построить для заданной функции «И-НЕ» и «ИЛИ-НЕ».
& и-не 1 или-не
Применяем два закона: закон двойной инверсии и правило Де-Моргана:
Пример построения схемы в базисе «И-НЕ»:
Пример построения схемы в базисе «или-не»:
х2 1 1 1
х3 4.2 Основные комбинационные (логические) схемы цифровых устройств.
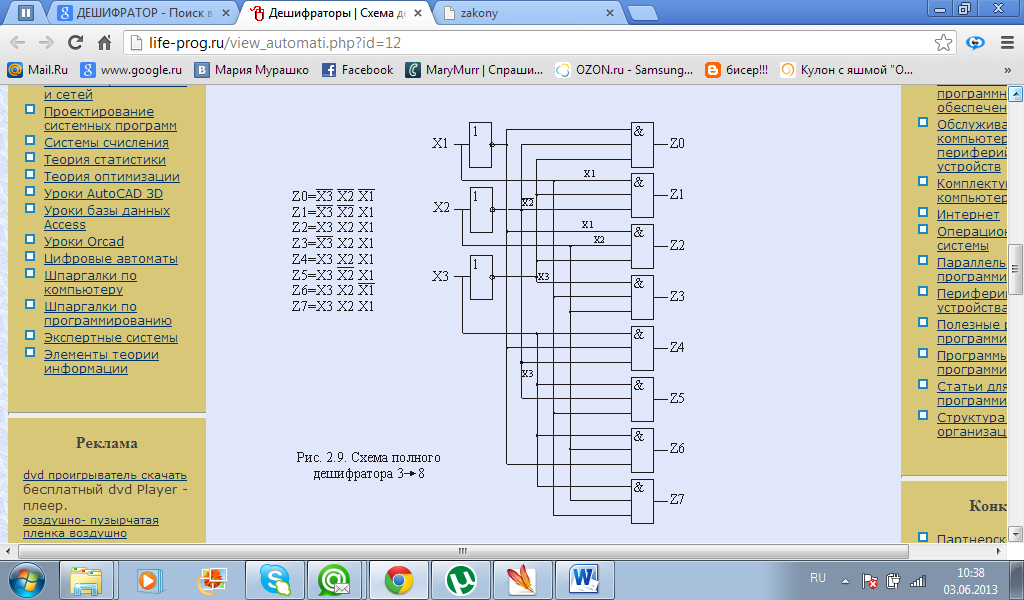
Дешифратор – имеет “m” – входов и 2m – выходов. При подаче на входы двоичной комбинации числа на выходе появляетя сигнал, номер которого соответствует входному числу.
Рассмотрим пример для 2-х кодового дешифратора. m = 2 2m = 4
деш у0 х0 у1 у2 у3 х1
Здесь 4 логических функции. Составим для них выражения.

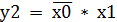
Рассмотрим пример для 3-х кодового дешифратора. m = 3 2m = 8
4.3 Электронные коммутаторы двоичных сигналов. а) простейший коммутатор – это схема “И”
х & Если А = 0; y = 0 y A = 1; y = x
A
б) мультиплексор. MUX; MS С помощью него осуществляется коммутация 2-ичных сигналов с одного из j – входов (Xj) на один выход у. На выход коммутируется вход с номером, соответствующ. двоичному числу Ао – Аj на адресных входах дешифратора.
х0 x1 коммут. у x2 x3 j = 2i
дешифр.
АоА1А2А3(Aj)
Рассмотрим пример для i = 2, j = 4
Для осуществления соответств. коммутаторов необходимо, чтобы управл. сигнал с выхода дешифратора соответствовал «1».
Ао А1
1 1 х0 & 1
x1 &
y x2 &
x3 &
MUX
Ao A1
в) демультиплексор.
Он осуществляет подключение 1-ого входа на один из j выходов с порядковым номером, соответствующему двоичному числу на адресных входах В.
у0 х у1
у2
дешифр. M = 2i,где М - индекс для Y.
Во В1 Вi
Пример:
y0
y1
y2
y3
Схемы сравнения двоичных чисел. 5.1 Схема, исключающая «ИЛИ» (полусумматор).
На выходе будет «1» тогда, когда на входах разные значения. х1 ПS=1 хg y
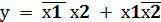
5.2 Схема сравнения. На выходе будет «1», если на обоих входах одинаковые числа.
5.3 Мажоритарный элемент – он выдает сигнал «у», если на входе будет двоичное число больше заданного М. Пусть М = 3
х2 ≥М х1 у х0
5.4 Цифровой компаратор – это схема сравнения двух одноразрядных чисел, которые не только определяют их равенства, но и превышение одного над другим.
х1>х2 х1=х2 х1<х2
у1 х1 у2 х2 у3
5.5 Коммутатор: последовательное соединение MUX и DMUX позволяет реализовать коммутатор.
5.6 Функциональные комбинационные схемы.
Двоичный сумматор.
1 1 1 1 – p – перенос 0 1 0 1 1 – 1-е слагаемое (х1) 0 0 1 0 1 – 2-е слаганмое (х2) ______________________________ 1 0 0 0 0 – сумма S сумматор полусумматор
а) полусумматор
х1 ПΣ сумма (S)
х2 перенос в старший разряд (Р)
1 х1
S
х2 1
В сумматоре должен быть дополнительный вход для переноса из младшего разряда.
Pi Σ X2 S S
X1 P Pi+1
HS S HS S
P P
Выше рассмотрен одноразрядный сумматор в) Схема многоразрядного сумматора.
х10 So х20
x11 x21
x21 x22
5.7 Действия над двоичными числами. Способ вычитания двоичных чисел с помощью суммирования с использованием дополнительного кода.
Умножение двоичных чисел.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 99; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.195.8 (0.008 с.) |

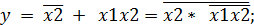
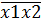
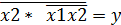

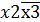 х1х2х3
х1х2х3  х2х3
х2х3 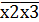 х1
х1 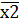 х3
х3  х3
х3 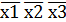
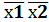
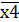
 (склеенный из 4-х углов)
(склеенный из 4-х углов)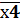 + х3 * х4 +
+ х3 * х4 + 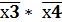
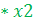 *
* 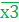 *х4*
*х4* 
 *х2*х3*
*х2*х3* 
 , логические схемы в базисах
, логические схемы в базисах