
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сигналы, которые действуют в течение всего периода элементарного символа.Содержание книги
Поиск на нашем сайте
1 0 1 1
б) Импульсные. Сигналы, у которых длительность элементарного сигнала минимальная, возможная, определяемая только длительностью переходных процессов.
Такие сигналы позволяют ускорить их обработку, однако к ним предъявляются жесткие требования к определению тактовых моментов (синхронизаций).
1.3. Двоичный код или слово. Как правило, для передачи какого-либо символа используется несколько двоичных сигналов. Каждый двоичный сигнал «1» или «0» называется битом. Количество бит для передачи какого-то одного символа называется разрядностью двоичной комбинации одного кодового слова. Коды могут быть:
2. Двоичная система счисления.
а) десятичная система счисления – характеризуется n – степенным полиномом.
…а* 104 + а* 103+ а* 102+ а* 101+ а* 100
1* 103 9* 102 5* 101 6* 100 = 1956
а – принимает значения от 0 до 10
б) степенной полином с основанием 2 – двоичная система счисления.
…а* 24 + а* 23 + а* 22 + а* 21+ а* 20; 1 * 24 + 0 * 23 + 1 * 22 + 0 * 21 + 1 * 10 = 16+0+4+0+1=2110=101012
а – может быть либо «0», либо «1». Способ перевода числа из десятичной в двоичную:
13: 2 = 6 (ост. 1) 6: 2 = 3 (ост. 0) 1 * 23 + 1 * 22 + 0 * 21 + 1 * 20 = 3: 2 = 1 (ост. 1) 8+4+0+1=1310=11012 1: 2 = 0 (ост. 1)
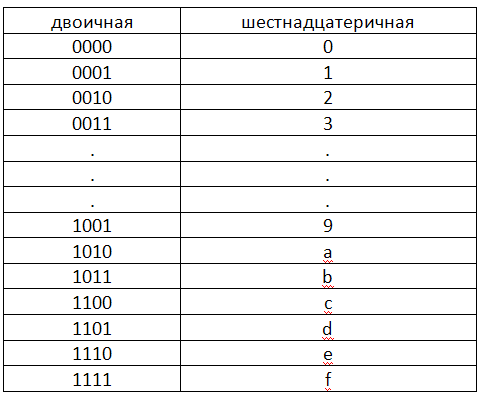
в) шестнадцатеричная система счисления Для передачи десятичных цифр необходимо четырехразрядная двоичная комбинация.
m = {log2M} {log210} = {3,5}=4 m – округляется до большего целого Элементы математического аппарата цифровой техники.
3.1 Булевы функции, законы, тождества и их применение.
Аргументы могут принимать значения «0», либо «1».
yi = F (x1; x2; ….xi)
Такие функции можно представить комбинационными схемами:
X1 Kc y1 X2 y2 X3 y3 Xi yi
Базисными (основными) логическими функциями являются схемы «И», «ИЛИ», «НЕ» на основе которых может быть построена сложная логическая функция (комбинационная логическая схема) часто используются универсальные логические схемы.
3.2 Законы и тождества Булевой алгебры. а) закон равнозначности: x + x = x, x * x = x, x*1 = x; б) закон противоречия:
в) закон двойного отрицания:
г) закон инверсии, правило Де-Моргана:
д) правило склеивания:
е) операция поглощения:
3.3 Построение логических функций и логических схем. Пусть задана таблица истинности:
Решение (алгоритм): 1. Выписываем строчки, где y = 1
2. Для каждой из этих строк записываем конъюнкцию аргумента. Если значение аргумента «0», то записываем аргумент (х) с инверсией:
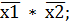
3. Записываем дизъюнкцию полученных конъюнкций: y =
4. Попытаемся упростить (минимизировать) полученную функцию: (члены минимизированной функции называется импликантами)
5. Проверка: х1 = 1; х2 = 0; у = 1; у = 1 + 1 * 0 = 1 + 0= 1
6. Построение логической схемы: Построим на основе основных («и», «или», «не») базисных функций.
& 1
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 88; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.201.180 (0.007 с.) |


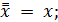
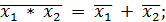

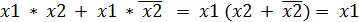
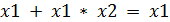



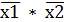 +
+ 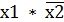 +
+ 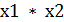 ;
;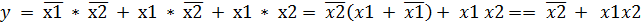
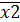 + x1x2 = y
+ x1x2 = y


