
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Имитационное моделирование объекта управленияСодержание книги
Поиск на нашем сайте
Имитационное моделирование объекта управления
С помощью пакета «MATLAB» построим переходную характеристику рассматриваемого объекта управления. Как было рассчитано выше, передаточная функция объекта управления имеет следующий вид: W0(p)= Для получения переходной характеристики объекта управления введем следующую команду «MATLAB»:
>> step(tf([1],[0.01, 0.06, 1]));
Получим следующее изображение переходной характеристики:
Рис 1.1. Переходная характеристика объекта управления с квантованием по времени
Согласно данному изображению переходной характеристики выберем интервал квантования Т0 = 0,1 c. Имитационное моделирование возмущающего воздействия и построение эмпирической оценки его корреляционной функции
Произведем моделирования возмущающего воздействия, действующего на заданный объект управления. Данное воздействие представляется как выходной сигнал формирующего фильтра, на вход которого подается «белый шум»:
Рис 3.1. Формирующий фильтр с «белым шумом» на входе
В нашем случае представим возмущающее воздействие двумя параллельно соединенными формирующими фильтрами:
Рис 3.2. Параллельное соединение двух формирующих фильтров Корреляционная функция возмущающего воздействия, показывающая, насколько проявляется зависимость процесса от предыдущих значений, имеет следующий вид: Rn(τ)= Подставим в данную корреляционную функцию исходные данные: Rn(τ)= = 2 Построим для наглядности графики корреляционных функций в системе «MATLAB»: >> syms t; >> ezplot(2*exp(-5*abs(t))) >> ezplot(4*exp(-1*abs(t))) >> ezplot(4*exp(-1*abs(t))+ 2*exp(-5*abs(t)))
Рис 3.3. Корреляционные функции отдельных составляющих блоков формирующих фильтров
Рис 3.4. Корреляционная функция формирующего фильтра По известной корреляционной функции Rnn(τ) найдем спектральную плотность возмущающего воздействия Snn(ω), характеризующую частотный состав процесса и определяющую распределение среднего значения мощности по спектру:
Имея выражение для спектральной плотности, можем определить теперь общий вид передаточной функции формирующего фильтра методом расщепления спектральной плотности:
Согласно определению белого шума его спектральная плотность является постоянной величиной. Пусть Sv(ω) = const = 1, тогда:
Рассчитаем тогда передаточные функции для каждого из формирующих фильтров и общую передаточную функцию формирующего фильтра:
Wфф(p) = Учитывая выбранный ранее шаг квантования (Т0 = 0,1 с), определим теперь дискретную передаточную функцию формирующего фильтра, используя следующую замену:
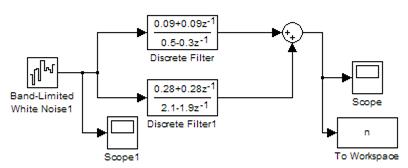
Gфф(z) = Построим в «Simulink» дискретную модель формирующего фильтра и снимем временные характеристики белого и окрашенного шума:
Рис 3.5. Модель формирующего фильтра
Рис 3.6. Белый шум
Рис 3.7. Окрашенный шум Построение дискретной модели переходом от дифференциального уравнения к разностному Передаточная функция рассматриваемого объекта управления имеет следующий вид: W0(p)= Из данного выражения получим дифференциальное уравнение, описывающее объект управления: 0,01 Перейдем теперь от дифференциального уравнения к разностному, используя левую разность и учитывая размер такта Т0 = 0,1 c: Δ2y(k) = y(k) - 2y(k-1) + y(k-2), Δy(k) =y(k) – y(k-1) =>
y(k) – 2y(k-1) + y(k-2) + 0,6y(k) – 0,6y(k-1)+y(k)=u(k) => 2,6y(k) - 2,6y(k-1) + y(k-2) = u(k) => y(k) = y(k)=y(k-1) - 0,4y(k-2) + 0,4u(k); В полученном выражении y(k) – выходной сигнал, u(k) – входной сигнал (единичное ступенчатое воздействие), k – отсчеты времени. C помощью данного выражения рассчитаем теперь значения на кривой разгона в моменты квантования, учитывая что график на рисунке 1.1 выходит из начала координат: y(0)=0; y(1)=y(Т0)=y(0) - 0,4y(-1) + 0,4u(1)= 0 – 0 + 0,4 = 0,4; y(2)=y(2Т0)=y(1) - 0,4y(0) + 0,4u(2)= 0,4 – 0 + 0,4 = 0,8; y(3)=y(3Т0)=y(2) - 0,4y(1) + 0,4u(3)= 0,8 – 0,16 + 0,4 = 1,04; y(4)=y(4Т0)=y(3) - 0,4y(2) + 0,4u(4)= 1,04 – 0,32 + 0,4 = 1,12; y(5)=y(5Т0)=y(4) - 0,4y(3) + 0,4u(5)= 1,12 – 0,42 + 0,4 = 1,1; y(6)=y(6Т0)=y(5) - 0,4y(4) + 0,4u(6)= 1,1 – 0,45 + 0,4 = 1,05; y(7)=y(7Т0)=y(6) - 0,4y(5) + 0,4u(7)= 1,05 – 0,44 + 0,4 = 1,01; y(8)=y(8Т0)=y(7) - 0,4y(6) + 0,4u(8)= 1,01 – 0,42 + 0,4 = 0,99; y(9)=y(9Т0)=y(8) - 0,4y(7) + 0,4u(9)= 0,99 – 0,4 + 0,4 = 0,99; y(10)=y(10Т0)=y(9) - 0,4y(8) + 0,4u(10)= 0,99 – 0,4 + 0,4 = 0,99; Чтобы получить передаточную функцию, применим к выражению для y(k) z-преобразование: Z{y(k)} = Z{y(k-1) - 0,4y(k-2) + 0,4u(k)}; Y(z) = Y(z)·z-1 – 0,4·Y(z)·z-2 +0,4·U(z) => Y(z)·(1 – z-1 + 0,4·z-2) = 0,4·U(z) => G0(z)= Рассчитаем статический коэффициент передачи объекта, подставив вместо z единицу: K0 =G0(1)=
Настройка системы с цировым ПИД-регулятором Сравнение полученных цифровых систем с разными регуляторами Рекомендации по выбору регулятора
Согласно результатам проведенных исследований по рассматриваемым критериям для данной системы лучше использовать цифровой ПИД-регулятор, обеспечивающий лучшие характеристики по сравнению с цифровым регулятором с минимальной обобщенной дисперсией, который показал недопустимые результаты. Список литературы
1. Чостковский Б.К. Методическое пособие. Имитационное моделирование оптимального управления стохастическим объектом.- Самара: СамГТУ.
Имитационное моделирование объекта управления
С помощью пакета «MATLAB» построим переходную характеристику рассматриваемого объекта управления. Как было рассчитано выше, передаточная функция объекта управления имеет следующий вид: W0(p)= Для получения переходной характеристики объекта управления введем следующую команду «MATLAB»:
>> step(tf([1],[0.01, 0.06, 1]));
Получим следующее изображение переходной характеристики:
Рис 1.1. Переходная характеристика объекта управления с квантованием по времени
Согласно данному изображению переходной характеристики выберем интервал квантования Т0 = 0,1 c.
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 306; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.29.190 (0.008 с.) |

 ;
;


 ;
; + 4
+ 4  = Rn1(τ)+ Rn2(τ)
= Rn1(τ)+ Rn2(τ)





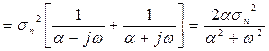 ;
;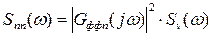 .
. ;
; ;
;  ;
;  ;
; = 0,9;
= 0,9;  = 0,2;
= 0,2;  ;
; = 2,8;
= 2,8;  = 1;
= 1;  ;
; +
+  ;
; ;
; ;
; =
=  ;
;  =
= 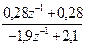 ;
; +
+  ;
;


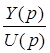 => (0,01p2+0,06p+1)·Y(p)=U(p);
=> (0,01p2+0,06p+1)·Y(p)=U(p); +0,06
+0,06  +y(t) = u(t);
+y(t) = u(t); +
+  + y(k) = u(k);
+ y(k) = u(k); +
+  + y(k) = u(k);
+ y(k) = u(k); =>
=> =
=  ;
; =1;
=1;


