Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Настройка ПИД-регулятора непрерывной модели системыСодержание книги
Поиск на нашем сайте
Рис 4.1.1. Схема непрерывной модели системы
Построим в «Simulink» непрерывную модель системы управления и произведем настройку непрерывного ПИД-регулятора. Настройку параметров ПИД-регулятора будем производить по кривым управляемого и возмущающего процессов, добиваясь их оптимального вида: x(t) = 1(t) => y(t) = h(t)
Рис 5.1.2. Схема настройки ПИД регулятора по управляемому процессу
n(t) = 1(t) => y(t) = yв(t)
Рис 4.1.3. Схема настройки ПИД регулятора по возмущающему процессу
Настройкой параметров ПИД-регулятора добьемся следующих наиболее оптимальных характеристик h(t) и yв(t):
Рис 5.1.4. Оптимальная характеристика h(t)
Рис 4.1.5. Оптимальная характеристика yв (t)
Приведенные выше характеристики были получены при следующих оптимальных значениях параметров ПИД-регулятора: Kp = 0,1; Tи = 0,1; Tд = 3; Следует отметить, что согласно характеристике, изображенной на рис. 4.1.4 возмущающее воздействие гасится при его прохождении через данную систему автоматического управления. Исследуем теперь дискретную модель системы автоматического управления с ПИД-регулятором.
Настройка ПИД-регулятора дискретной модели системы
Рис 4.2.1. Схема дискретной модели системы
Исследуем дискретную модель системы с ПИД-регулятором, параметры которого попытаемся получить пересчетом параметров непрерывного регулятора из п. 4.1. q0 = Kp(1 + q1 = - Kp(1 - q2 = Kp Построим в «Simulink» модель цифровой системы с рассчитанным регулятором и построим кривые управляемого и возмущающего процессов:
Рис 4.2.2. Схема настройки ПИД регулятора по управляемому процессу
Рис 4.2.3. Схема настройки ПИД регулятора по возмущаемому процессу При рассчитанных параметрах цифрового ПИД-регулятора получаем следующие характеристики h(k) и yв(k):
Рис 4.2.4. Характеристика h(k) системы с цифровым регулятором, рассчитанным по параметрам непрерывного
Рис 4.2.5. Характеристика yв(k) системы с цифровым регулятором, рассчитанным по параметрам непрерывного
Представленные на рисунках характеристики являются наиболее оптимальными для данной цифровой системы с цифровым ПИД-регулятором.
Настройка системы с цифровым регулятором с минимальной обобщенной дисперсией Найдем передаточную функцию регулятора с минимальной обобщенной дисперсией, воспользовавшись известным соотношением: Gр (z)= Gо (z) = Gфф (z) = = = => Gр(z)= = = =
Сравнение полученных цифровых систем с разными регуляторами Характеристики по возмущающему воздействию Сравним выходные характеристики систем по возмущающему воздействию:
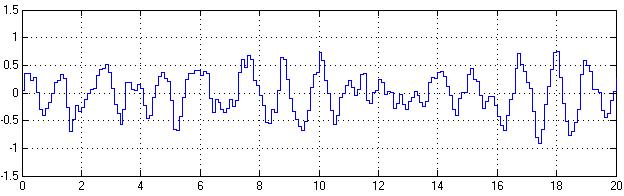
Рис 6.1.1. Выходная характеристика по возмущающему воздействию системы без регулятора
Рис 6.1.2. Выходная характеристика по возмущающему воздействию системы с ПИД-регулятором
Рис 6.1.3. Выходная характеристика по возмущающему воздействию системы с регулятором с минимальной обобщенной дисперсией
Из рисунков очевидно, что система с цифровым ПИД-регулятором (рис.6.1.2) гораздо эффективнее справляется с возмущениями, чем система с цифровым регулятором с обобщенной дисперсией (рис. 6.1.3), которая фактически повторяет возмущающее воздействие.
Оценка по минимуму квадратичной интегральной оценки Оценку по данному критерию произведем, построив в «Simulink» все три модели с использованием блока «Display»:
Рис 6.2.1. Исходная система
Рис 6.2.2. Система с ПИД-регулятором
Рис 6.2.2. Система с регулятором с минимальной обобщенной дисперсией
Из рисунков видно, что лучшей по данному критерию является система с ПИД-регулятором. Рекомендации по выбору регулятора
Согласно результатам проведенных исследований по рассматриваемым критериям для данной системы лучше использовать цифровой ПИД-регулятор, обеспечивающий лучшие характеристики по сравнению с цифровым регулятором с минимальной обобщенной дисперсией, который показал недопустимые результаты. Список литературы
1. Чостковский Б.К. Методическое пособие. Имитационное моделирование оптимального управления стохастическим объектом.- Самара: СамГТУ.
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 399; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.117.77 (0.006 с.) |

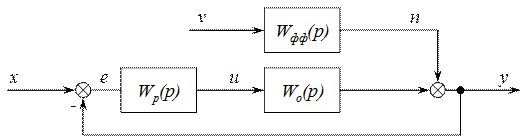





 ) = 0,1(1+ 30) = 3,1;
) = 0,1(1+ 30) = 3,1; +
+  ) = -0,1(1 – 1 + 60) = - 6;
) = -0,1(1 – 1 + 60) = - 6;



 ;
; =
=  ;
;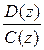 =
=  +
+  =
= =
= =
=  ;
; =
= =
= =
= ;
;