
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Форма и размеры Земли. Системы координат.Содержание книги
Поиск на нашем сайте ИНЖЕНЕРНАЯ ГЕОДЕЗИЯ
Учебное пособие
Часть I
САНКТ-ПЕТЕРБУРГ УДК 528.48
Инженерная геодезия. Учебное пособие, часть I / Е.С. Богомолова, М.Я. Брынь, В.В. Грузинов, В.А. Коугия, В.И. Полетаев; под ред. В.А. Коугия. – СПб.: Петербургский гос. ун-т путей сообщения, 2006. - с.
Изложены предмет и задачи инженерной геодезии, сведения о системах координат и высот, методах построения плановых и высотных геодезических сетей, элементы теории погрешностей измерений, приборы и методы, применяемые для измерения углов и расстояний, приборы и методы нивелирования. Разделы 1, 6 пособия написаны М.Я. Брынем, 2, 9 – Е.С. Богомоловой, 3 – В.В. Грузиновым, 4, 8 – В.А. Коугия, 5, 7 – В. И. Полетаевым. Предназначено для студентов, обучающихся по железнодорожным и строительным специальностям.
ПРЕДМЕТ ИНЖЕНЕРНОЙ ГЕОДЕЗИИ Геодезия – наука, изучающая фигуру и внешнее гравитационное поле Земли и разрабатывающая методы создания систем координат, определения положения точек на Земле и околоземном пространстве, изображения земной поверхности на картах. Научными задачами геодезии являются: - установление систем координат; - определение формы и размеров Земли и ее внешнего гравитационного поля и их изменений во времени; - проведение геодинамических исследований (определение горизонтальных и вертикальных деформаций земной коры, движений земных полюсов, перемещений береговых линий морей и океанов и др.). Научно-технические задачи геодезии в обобщенном виде заключаются в следующем: - определение положения точек в выбранной системе координат; - составление карт и планов местности разного назначения; - обеспечение топографо-геодезическими данными нужд обороны страны; - выполнение геодезических измерений для целей проектирования и строительства, землепользования, кадастра, исследования природных ресурсов и др. Геодезия в процессе своего развития разделилась на ряд научных дисциплин: высшую геодезию, топографию, фотограмметрию, картографию, космическую геодезию, морскую геодезию, инженерную геодезию. Особое место в этом ряду занимает инженерная геодезия, которая разрабатывает методы геодезического обеспечения изысканий, проектирования, строительства и эксплуатации инженерных сооружений: железных и автомобильных дорог, мостов, тоннелей, трубопроводов, промышленных и гражданских зданий, систем водоснабжения и водоотведения и др. Основными задачами инженерной геодезии являются: - топографо-геодезические изыскания, в ходе которых выполняется создание на объекте работ геодезической сети, топографическая съемка, геодезическая привязка точек геологической и геофизической разведки; - инженерно-геодезическое проектирование, включающее разработку генеральных планов сооружений и их цифровых моделей; геодезическую подготовку проекта для вынесения его в натуру, расчеты по горизонтальной и вертикальной планировке, определению площадей, объемов земляных работ и др.; - геодезические разбивочные работы, включающие создание на объекте геодезической разбивочной сети и последующий вынос в натуру главных осей сооружения и его детальную разбивку; - геодезическая выверка конструкций и технологического оборудования при установке их в проектное положение; - наблюдения за деформациями сооружений, определяющие осадки оснований и фундаментов, плановые смещения и крены сооружений. Геодезическое обеспечение строительства и эксплуатации современных инженерных сооружений связано с необходимостью выполнения точных измерений, служащих определению координат и высот геодезических пунктов, составлению топографических карт и планов, продольных профилей трасс; наблюдению за деформациями сооружений. Для обеспечения необходимой точности измерения выполняются высокоточными геодезическими приборами: теодолитами – угловые измерения; светодальномерами – линейные измерения; электронными тахеометрами – угловые и линейные измерения с решением различных инженерно-геодезических задач; нивелирами – определение превышений. При определении положения объектов используется аппаратура, работающая по сигналам спутниковых навигационных систем, при выполнении топографической съемки местности находят применение лазерные сканеры. Обработка результатов геодезических измерений выполняется на современных компьютерах с использованием развитого программного обеспечения. К числу таких программных продуктов относятся геоинформационные системы, служащие сбору, обработке, систематизации, отображению и анализу картографической информации. Состав геодезических работ, их точность, используемые методы и приборы различаются в зависимости от особенностей объекта. Так, при выполнении изысканий железной дороги создают геодезическую сеть, опираясь на которую составляют топографические карты и планы. На картах и планах выполняют предварительное трассирование дороги, окончательное положение которой выбирают в поле. Затем делают съемку трассы и получают необходимые для проектирования дороги профиль трассы и ситуационный план полосы местности. Для обеспечения безопасного движения поездов вдоль железной дороги создают высокоточную геодезическую сеть (так называемую, реперную систему), опираясь на которую выполняют работы по реконструкции и ремонту пути, по оперативному контролю его геометрических параметров, по наблюдениям за деформациями пути, земляного полотна и искусственных сооружений. В процессе строительства и по мере завершения отдельных его этапов выполняются исполнительные съемки, целью которых является установление точности вынесения проекта сооружения в натуру, выявление отклонений, допущенных в процессе строительства, а также определение фактических координат и высотных отметок построенных объектов, размеров его отдельных частей.
ФОРМА И РАЗМЕРЫ ЗЕМЛИ. СИСТЕМЫ КООРДИНАТ. ВЫСОТЫ
Форма и размеры Земли Изучение формы и размеров Земли включает решение двух задач. Это - установление некоторой сглаженной, обобщенной, теоретической фигуры Земли и определение отклонений от нее фактической физической поверхности. Учитывая, что поверхность океанов и морей составляет 71% поверхности Земли, а поверхность суши - только 29%, за теоретическую фигуру Земли принято тело, ограниченное поверхностью океанов в их спокойном состоянии, продолженной и под материками, и называемое геоидом. Поверхность, в каждой своей точке перпендикулярная к отвесной линии (направлению силы тяжести), называется уровенной поверхностью. Из множества уpовенных поверхностей одна совпадает с поверхностью геоида. Из-за неравномерности распределения масс в земной коре геоид имеет неправильную геометрическую форму, и его поверхность нельзя выразить математически, что необходимо для решения геодезических задач. При решении геодезических задач геоид заменяют близкими к нему геометрически правильными поверхностями. Так, для приближенных вычислений Землю принимают за шар с радиусом 6371 км. Ближе к форме геоида подходит эллипсоид – фигура, получаемая вращением эллипса (рис. 2.1) вокруг его малой оси. Размеры земного эллипсоида характеризуют следующими основными параметрами: a - большая полуось, b - малая полуось, a - полярное сжатие и e – первый эксцентриситет меридианного эллипса, где
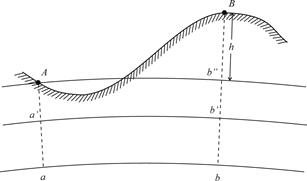
Различают общеземной эллипсоид и референц-эллипсоид. Центр общеземного эллипсоида помещают в центре масс Земли, ось вращения совмещают со средней осью вращения Земли, а размеры принимают такие, чтобы обеспечить наибольшую близость поверхности эллипсоида к поверхности геоида. Общеземной эллипсоид используют при решении глобальных геодезических задач, и в частности, при обработке спутниковых измерений. В настоящее время широко пользуются двумя общеземными эллипсоидами: ПЗ-90 (Параметры Земли 1990 г, Россия) и WGS-84 (Мировая геодезическая система 1984 г, США). Референц-эллипсоид – эллипсоид, принятый для геодезических работ в конкретной стране. С референц-эллипсоидом связана принятая в стране система координат. Параметры референц-эллипсоида подбираются под условием наилучшей аппроксимации данной части поверхности Земли. При этом совмещения центров эллипсоида и Земли не добиваются. В России с 1946 г. в качестве референц-эллипсоида используется эллипсоид Красовского с параметрами: а = 6 378 245 м, a = 1/ 298,3. Системы высот Счет высот в инженерной геодезии ведут от одной из уровенных поверхностей. Высотой точки называют расстояние по отвесной линии от точки до уровенной поверхности, принятой за начало счета высот. Если высоты отсчитывают от основной уровенной поверхности, то есть от поверхности геоида, их называют абсолютными высотами. На рис. 2.5 отрезки отвесных линий Аа и Вв - абсолютные высоты точек А и В. Если за начало счета высот выбрана какая-либо другая уровенная поверхность, то высоты называют условными. На рис. 2.5 отрезки отвесных линий Аа¢ и Вв¢ - условные высоты точек А и В. В России принята Балтийская система высот. Счет абсолютных высот ведут от уровенной поверхности, проходящей через нуль Кронштадтского футштока. Численное значение высоты принято называть отметкой. Например, если высота точки А равна HА = 15,378 м, то говорят, что отметка точки равна 15,378 м.
Разность высот двух точек называется превышением. Так, превышение точки В над точкой А равно hAB = HВ - HA. Зная высоту точки А, для определения высоты точки В на местности измеряют превышение hAB. Высоту точки В вычисляют по формуле HВ = HA + hAB. Измерение превышений и последующее вычисление высот точек называется нивелированием. Абсолютную высоту точки следует отличать от ее геодезической высоты, то есть высоты, отсчитываемой от поверхности земного эллипсоида (см. раздел 2.2). Геодезическая высота отличается от абсолютной высоты на величину отклонения поверхности геоида от поверхности эллипсоида. В заключение отметим, что точное определение положения поверхности геоида в области материков невозможно. Поэтому в России принято отсчитывать высоты от близкой к геоиду, но доступной точному определению вспомогательной поверхности, названной квазигеоидом. Высоты, отсчитываемые от поверхности геоида, называются ортометрическими высотами, а отсчитываемые от поверхности квазигеоида – нормальными высотами. На результаты измерений, выполняемых в инженерной геодезии, различия в двух названных системах высот влияния не оказывают, и в дальнейшем мы их различать не будем, а будем пользоваться введенным выше обобщенным понятием – абсолютные высоты.
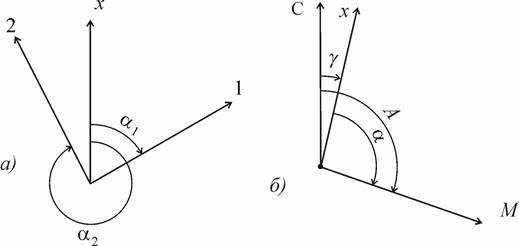
Углы ориентирования Ориентировать линию – значит определить её направление относительно исходного направления, например, меридиана или оси абсцисс х системы плоских прямоугольных координат. Угол, измеряемый по ходу часовой стрелки от северного направления меридиана до заданного направления, называется азимутом. Если исходным направлением служит геодезический меридиан, то азимут называют геодезическим азимутом. Если – астрономический, то - астрономическим азимутом. Обобщением обоих понятий служит термин - географический азимут или просто - азимут. Значения азимута лежат в пределах от 0° до 360°. На рис. 3.1, а обозначено: С – северное направление меридиана, угол А 1 – азимут направления на точку 1 и А 2 – азимут направления на точку 2.
Рис. 3.1. Углы ориентирования: а - азимуты географические; б - магнитный азимут На местности азимут заданного направления можно определить астрономическим методом - измерив горизонтальный угол между направлением на небесное светило (Солнце, звезду) и заданным направлением. Зная азимут светила, вычисляемый с использованием астрономического ежегодника, и измеренный угол, соображают азимут заданного направления. Угол, отсчитываемый от северного направления магнитной стрелки до заданного направления, называется магнитным азимутом. Магнитная стрелка компаса отклоняется от направления истинного меридиана на угол d, который называется склонением магнитной стрелки (рис. 3.1, б). Если северный конец магнитной стрелки отклоняется от меридиана к востоку, то склонение называют восточным и считают положительным, а если - к западу, то называют западным и считают отрицательным. Азимут с магнитным азимутом связывает формула:
где А - азимут, А м - магнитный азимут и d – склонение магнитной стрелки. Магнитные азимуты в геодезии измеряют буссолью (рис. 3.2). Однако точность этих измерений невысока (несколько минут), так как склонение магнитной стрелки непостоянно. На территории России оно меняется от места к месту в пределах от –15° до 25°. В аномальных районах (например, в районе Курской магнитной аномалии) эти изменения так велики, что магнитной стрелкой пользоваться нельзя. Кроме того, склонение изменяется во времени, испытывая суточные, годовые и вековые изменения.
Углом ориентирования, применяемым при использовании системы плоских прямоугольных координат Гаусса-Крюгера, является дирекционный угол. Дирекционным углом называется угол между северным направлением осевого меридиана или линии ему параллельной и заданным направлением (рис. 3.3). Угол g между северным направлением меридиана и направлением оси абсцисс х прямоугольных координат (то есть линии, параллельной осевому меридиану) называется с ближением меридианов.
Рис. 3.3. Углы ориентирования: а - дирекционные углы a1, a2; б - азимут A и дирекционный угол a
При отклонении оси абсцисс от меридиана к востоку, сближение меридианов считают положительным, а при отклонении к западу - отрицательным. При этом справедлива формула (рис. 3.3 б) А = a + g, где a - дирекционный угол, g - сближение меридианов. ПЛАН И КАРТА
План, карта, цифровая модель местности Планом называется уменьшенное подобное изображение горизонтальной проекции небольшого участка местности. Для составления плана местности расположенные на ней точки проецируют на уровенную поверхность по направлению отвесных линий. Ввиду малости участка отвесные линии оказываются практически параллельными, а фрагмент уровенной поверхности может рассматриваться как плоскость. Полученную проекцию местности уменьшают и изображают на плане. Степень уменьшения характеризуется масштабом плана. Масштабом называется отношение длины отрезка на плане к длине горизонтальной проекции соответствующего отрезка местности. Масштаб записывают в виде дроби с числителем, равным единице, и знаменателем, показывающим, во сколько раз уменьшены на плане длины линий. При строительстве железных дорог для выбора варианта трассы используют планы масштабов 1:2000 и 1:5000, для рабочего проектирования - 1:1000 и 1:2000, для проектирования мостов, тоннелей, станций - 1:500 ¸ 1:2000. Наряду с представлением масштаба в виде дроби (численного масштаба) пользуются именованным масштабом - его словесным описанием, например: “в одном сантиметре 20 метров”, что соответствует масштабу 1:2000. Для измерения расстояний на плане, под его нижней рамкой, помещают линейный масштаб (рис. 4.1), на котором несколько раз отложено одно и то же расстояние, называемое основанием масштаба и равное обычно 2 см. Крайнее левое основание делят на более мелкие отрезки. Деления линейного масштаба оцифровывают в метрах.
Рис. 4.1 Линейный масштаб Картой называют уменьшенное и обобщённое изображение на плоскости всей земной поверхности или значительных её частей. Для изготовления карты объекты местности проецируют на поверхность земного эллипсоида и полученное изображение переносят на плоскость. Такой перенос невозможно выполнить без искажений. Каковы будут искажения, определяется картографической проекцией – законом перехода от геодезических координат объектов к плоским координатам карты. В геодезии чаще всего пользуются равноугольными (или иначе - конформными) проекциями, сохраняющими без искажений углы и очертания малых объектов. Карты различаются также по виду изображения на них меридианов и параллелей. В конических проекциях параллели изображаются концентрическими окружностями, а меридианы – радиальными прямыми, углы между которыми пропорциональны разностям долгот. Если при этом углы между изображениями меридианов равны разностям долгот, проекция называется азимутальной. В цилиндрических проекциях линии меридианов и параллелей изображаются взаимно перпендикулярными прямыми. Топографические карты в России издают в поперечной цилиндрической проекции Гаусса - равноугольной проекции, в которой прямыми линиями без искажений изображаются осевой меридиан зоны и экватор. В условиях применения компьютерных технологий, наряду с изображениями местности на бумажных носителях - картами и планами, используются их цифровые аналоги. Цифровой моделью местности (ЦММ) называется представленное в виде цифровых кодов и хранимое на магнитных носителях логико-математическое описание местности, адекватное по содержанию плану местности. Основным содержанием ЦММ является топографическая информация: координатыи высоты точек, очертания объектов, их свойства. ЦММ содержит и общую информацию - название участка, систему координат и высот и др. Цифровой картой называют цифровую модель значительного участка земной поверхности, сформированную с учётом генерализации изображаемых объектов и принятой картографической проекции. Электронной картой называется изображение местности на экране дисплея, полученное на основе цифровой карты. 4.2. Разграфка и номенклатура топографических карт и планов Топографические карты издают на листах со сторонами 40–50 см. В основу разграфки (нарезки) карт положена карта масштаба 1:1000000. Она издается на листах размерами 4° по широте и 6° по долготе. Множество листов такой карты по направлению параллелей образует ряды шириной по 4°, а по направлению меридианов - колонны шириной по 6°. Таблица 4.1
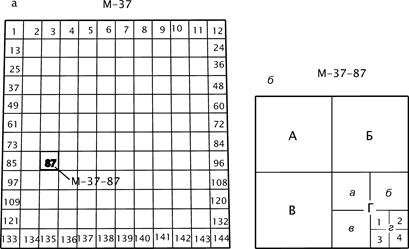
Ряды обозначают заглавными буквами латинского алфавита A, B, C, D,..., начиная от экватора по направлениям к северу и югу (табл. 4.1). Колонны нумеруют арабскими цифрами 1, 2,..., 60, начиная от меридиана 180° в направлении с запада на восток. Каждому листу карты масштаба 1:1000000 присвоен номенклатурный номер, состоящий из буквы соответствующего ряда и номера колонны, например, M -42. Для карт масштаба 1:500000 лист масштаба 1:1000000 меридианом и параллелью делят на 4 листа, обозначая их прописными буквами А, Б, В, Г. Номенклатурные номера листов карты образуют добавлением соответствующей буквы к номенклатурному номеру листа масштаба 1:1000000 (например, M -42-Г). Для карт масштаба 1:200000 лист масштаба 1:1000000 делят на 36 листов, нумеруя их римскими цифрами I, II,..., XXXVI. Для карт масштаба 1:100000, разделив лист масштаба 1:1000000 по широте и долготе на 12 частей, получают границы 144 листов (рис. 4.2, а), которые нумеруют цифрами 1, 2,..., 144. Номенклатура каждого листа складывается из номенклатуры листа масштаба 1:1000000 и номера листа. На рисунке выделен лист M -37-87.
Рис. 4.2. Разграфка листов карт масштабов: а – 1:100000; б – 1:50000, 1:25000, 1:10000. Разграфка карт масштабов 1:50000, 1:25000 и 1:10000 формируется делением на четыре части листа более мелкого масштаба (соответственно - 1:100000, 1:50000, 1:25000) и добавлением к номенклатуре предыдущего масштаба соответствующего знака, как показано на рис. 4.2, б и в табл. 4.2.
Таблица 4.2
Для планов масштабов 1:5000 и 1:2000 применяется два вида разграфки - трапециевидная, в которой рамками планов служат параллели и меридианы, и прямоугольная, в которой рамки совмещают с линиями сетки прямоугольных координат. При трапециевидной разграфке границы листов планов масштаба 1:5000 получают делением листа масштаба 1:100000 на 256 частей (16´16), которые нумеруют от 1 до 256. Номенклатура, например листа №70, записывается так M -37-87(70). Разграфку листов масштаба 1:2000 получают делением листа масштаба 1:5000 на 9 частей (3´3) и обозначают добавлением буквы русского алфавита, например, M- 37-87(70-и). Прямоугольная разграфка применяется для планов населённых пунктов и для участков площадью менее 20 км2, а также для планов масштабов 1:1000 и 1:500. При съёмке отдельного участка план может быть составлен и на листе нестандартного формата.
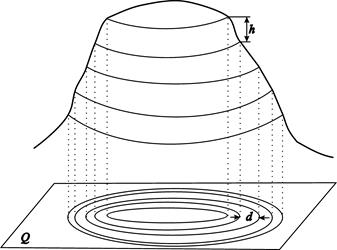
4.3. Условные знаки топографических карт и планов Рамки карты и координатные линии. Листы топографических карт имеют три рамки: внутреннюю, минутную и внешнюю. Внутреннюю рамку образуют отрезки параллелей, ограничивающих площадь карты с севера и юга, и отрезки меридианов, ограничивающих её с запада и востока. Значения широт и долгот на линиях внутренней рамки связаны с номенклатурой карты и написаны в каждом её углу. Между внутренней и внешней рамками помещена минутная рамка, на которой нанесены деления, соответствующие одной минуте широты (слева и справа) и долготы (наверху и внизу). Точками на рамке отмечены десятки секунд. Система прямоугольных координат на карте представлена километровой сеткой, образованной проведенными через 1 км координатными линиями x и y. Значения x и y, выраженные в километрах, надписаны на выходах линий за внутреннюю рамку карты. Планы масштабов 1:5000-1:500 с прямоугольной разграфкой имеют только сетку прямоугольных координат. Ее линии проведены через 10 см. Условные знаки. На планах и картах объекты местности изображают условными знаками. Условные знаки различают контурные, внемасштабные и линейные. Контурными условными знаками изображают объекты, форма и размеры которых могут быть переданы в масштабе плана (карты). К ним относятся земельные угодья (леса, сады, пашни, луга), водоёмы, а для более крупных масштабов - здания, сооружения. Очертания объектов (контуры) на плане показывают точечным пунктиром или линиями определённой толщины и цвета. Внутри контура помещают знаки, указывающие характер объекта. Внемасштабными условными знаками изображают объекты, которые необходимо нанести на план, но невозможно изобразить в масштабе (бензоколонки, колодцы, пункты геодезической сети и др.). Линейными условными знаками изображают объекты, длина которых выражается в масштабе плана, а ширина не выражается (линии электропередач и связи, трубопроводы, ограды, тропы). Для отражения характеристик изображаемых объектов многие условные знаки сопровождаются пояснительными подписями. Так, при изображении железной дороги указывают высоту насыпи и глубину выемки, ширину колеи на узкоколейной дороге. При изображении шоссе указывают его ширину и материал покрытия; при изображении линий связи – число проводов и их назначение; при изображении лесов – породу деревьев, среднюю высоту, толщину стволов и расстояние между деревьями. Изображение рельефа. На картах и планах рельеф изображают с помощью горизонталей, высотных отметок и условных знаков. Горизонтали - линии сечения земной поверхности равноотстоящими уровенными поверхностями. Иными словами, горизонтали - это линии равных высот. Горизонтали, подобно другим точкам местности, проецируют на уровенную поверхность Q и наносят на план (рис. 4.3).
Рис. 4.3. Горизонтали: h – высота сечения рельефа; d – заложение Разность h высот смежных горизонталей, равная расстоянию между секущими поверхностями, называется высотой сечения рельефа. Значение высоты сечения подписывают у нижней рамки плана. Горизонтальное расстояние между соседними горизонталями называется заложением. Минимальным в данном месте является заложение, перпендикулярное к горизонталям, – заложение ската. Чем меньше заложение ската, тем круче скат. Направление ската указывают бергштрихами - короткими штрихами у некоторых горизонталей, направленными в сторону спуска. На отдельных горизонталях в их разрывах пишут их высоту так, чтобы верх цифр указывал в сторону подъёма. Горизонтали с круглыми значениями высот делают утолщёнными, а для отражения деталей рельефа используют полугоризонтали – штриховые линии, соответствующие половине высоты сечения рельефа, а также вспомогательные горизонтали с короткими штрихами, проводимые на произвольной высоте. Изображение рельефа горизонталями дополняется вписыванием на план отметок высот около характерных точек рельефа и специальными условными знаками, изображающими обрывы, скалы, овраги и т. п. Основными формами рельефа являются гора, котловина, хребет, лощина и седловина (рис. 4.4).
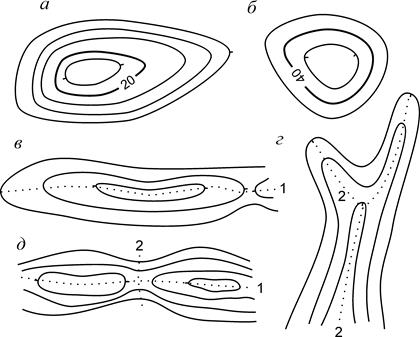
Рис. 4.4. Основные формы рельефа: а – гора; б – котловина; в – хребет; г – лощина; д – седловина; 1 – водораздельная линия; 2 – водосливная линия.
Гора (возвышенность, холм, курган, сопка) изображается замкнутыми горизонталями с бергштрихами, обращёнными наружу (рис. 4.4, а). Характерными точками горы являются её вершина и точки у подошвы. Котловина (впадина) тоже изображается замкнутыми горизонталями, но с бергштрихами, обращёнными внутрь (рис. 4.4, б). Характерными точками котловины являются точки на её дне и вдоль бровки. Хребет - вытянутая возвышенность. Изображается огибающими гребень хребта и идущими по его скатам вытянутыми горизонталями (рис. 4.4, в). Бергштрихи, как и у горы, обращены наружу. Характерной линией хребта является проходящая вдоль его гребня водораздельная линия. Лощина (долина, ущелье, овраг, балка) – вытянутое в одном направлении углубление. Изображается вытянутыми, горизонталями с бергшрихами, обращёнными внутрь (рис. 4.4, г). Характерной линией лощины является водосливная линия (тальвег) - линия, по которой сбегает вода. Седловина (перевал) – понижение между двумя возвышенностями (рис. 4.4, д). По обе стороны к седловине примыкают лощины. Седловина – это место пересечения водораздельной и водосливной линий. ГЕОДЕЗИЧЕСКИХ ИЗМЕРЕНИЙ Погрешности измерений Геодезические работы связаны с выполнением измерений различных величин - расстояний, превышений, углов и др. Измерения могут выполняться непосредственным сравнением измеряемой величины с единицей меры – прямые измерения, и посредством ее вычисления как функции других непосредственно измеренных величин – косвенные измерения. Результаты измерений всегда содержат некоторые погрешности. Погрешностью Δ называют отклонение результата измерения l от истинного значения измеряемой величины Х. Δ = l – Х (5.1) Погрешности проявляются, например, при многократном измерении одной и той же величины – получаемые результаты всегда несколько различаются между собой, и значит, неизбежно отличаются от истинного значения, т.е. содержат погрешности. Причинами, порождающими погрешности результатов измерений, являются несовершенство измерительных приборов, несовершенство органов чувств наблюдателя, внешние условия, влияющие на измерения. Измерения, выполненные однотипными приборами, одинаковыми методами и в одинаковых условиях, принято считать равноточными, а выполненные разными приборами и методами, в разных условиях считают неравноточными. Различают три основных вида погрешностей: случайные, систематические и грубые. Грубые погрешности – необычно большие погрешности, вызванные небрежностью наблюдателя, неисправностью прибора или резким отклонением от нормы условий измерений. Грубые погрешности выявляют путем выполнения и анализа избыточных измерений. Результаты измерений, содержащие грубые погрешности, отбрасывают, бракуют. Систематические погрешности – такие, которые при повторных измерениях остаются постоянными, или изменяются закономерным образом. Причины и закономерности появления систематических погрешностей должны быть изучены, и сами погрешности исключены из результатов измерений путем введения соответствующих поправок, применением надлежащих методик измерений, юстировкой приборов. Случайные погрешности – такие, которые при повторных измерениях изменяются случайным образом. Ни знак, ни значение случайной погрешности предвидеть невозможно. Поэтому невозможно исключить случайные погрешности из результатов измерений. Можно лишь при обработке измерений ослабить их влияние. Пути к такому ослаблению указывает теория погрешностей измерений. В дальнейшем будем полагать, что результаты измерений свободны от грубых и систематических и содержат только случайные погрешности. Измеренных величин. В практике геодезических измерений определяемые величины обычно являются функциями других, непосредственно измеряемых величин. Рассмотрим функцию u независимых переменных x, y, z, … u = f (x,y,z…). (5.5) Продифференцируем функцию (5.5) по всем переменным и заменим дифференциалы du, dx, dy, dz, …. погрешностями D u, D x,D y,D z, ….
Получили выражение случайной погрешности D u в зависимости от случайной комбинации погрешностей D x,D y,D z, …. Положим, что имеем n таких комбинаций, которым соответствует n выражений:
Возведем полученные выражения в квадрат, сложим и разделим на n:
где квадратными скобками обозначены суммы. Устремим число комбинаций в бесконечность (n ® ¥) и, воспользовавшись выражениями (5.4) и (5.3), получим:
Итак, квадрат средней квадратической погрешности функции общего вида равен сумме квадратов произведений частных производных по каждой переменной, умноженных на их средние квадратические погрешности. Частные случаи. 1. Функция u является суммой переменных x, y, z: u = x + y + z. В этом случае
2. Функция u является разностью переменных x и y: u = x - y. В этом случае
3. Функция u имеет вид: u = k× x, где k – постоянный множитель. Теперь mu = k× mx. 4. Функция u является линейной функцией от x, y, z, …: u = k 1 x + k 2 y + k 3 z …, где ki постоянные множители. Теперь частные производные равны
Рассмотрим примеры. Пример 1. Определить среднюю квадратическую погрешность превышения, вычисленного по горизонтальному расстоянию d =124,16 м и углу наклона n=2°16´, если md = 0,06 м, а m n = 1´. Превышение вычисляют по формуле h = d tgν. Продифференцируем формулу по переменным d и n:
Используя формулу общего вида (5.6) получим
Подставляя исходные данные, найдем
где 3438¢ - число минут в радиане. И окончательно mh =0,036.м. Пример 2. При геометрическом нивелировании (см. раздел 9.2) превышение вычисляют как разность отчетов по рейкам h = a - b. Отчеты берут с точностью ma = mb = 2 мм. Находим среднюю квадратическую погрешность превышения
Пример 3. Выведем формулу допустимой угловой невязки замкнутого теодолитного хода (см. раздел 9.4). Невязку вычисляют по формуле f b= b1+ b2+ ¼+ b n -180°(n -2), где b i – измеренные углы (i = 1, 2, ¼, n) и n – их число. Невязка - результат погрешностей в углах b i< |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 932; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.013 с.) |

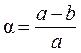 и
и  .
.





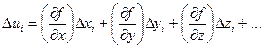 (i = 1, 2, …, n)
(i = 1, 2, …, n)
 ,
, ,
,  ,
,  ,
,  ,
,  . И окончательно
. И окончательно (5.6)
(5.6) =1,
=1,  =1,
=1,  =1. Следовательно
=1. Следовательно =
=  +
+  +
+  .
. =1,
=1,  =-1. Следовательно
=-1. Следовательно = k 2×
= k 2×  и
и = k 1,
= k 1,  = k 3. Поэтому
= k 3. Поэтому .
. ,
,  .
.

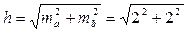 = 2,8 мм
= 2,8 мм


