
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
III. 1. Регулярная поверхность.III.1. РЕГУЛЯРНАЯ ПОВЕРХНОСТЬ. На евклидовой плоскости
плоской области
Эти функции непрерывны, ввиду того, что отображение
Отображение
Задается поверхность векторной функцией
Поверхность Наложим на функцию (1) (2) Векторы
Поверхность, заданная векторной функцией с указанными условиями, называется регулярной класса III.2. ЛИНИИ НА ПОВЕРХНОСТИ. Фиксируя на поверхности - - Всякие две -линии и всякие две
Если в области
Это произвольная линия на поверхности. III.3. КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И НОРМАЛЬ ПОВЕРХНОСТИ. Пусть
т.е. вектор касательной III.3.1. ТЕОРЕМА. Регулярная поверхность Пусть
Прямая
III.4. ПЕРВАЯ ОСНОВНАЯ КВАДРАТИЧНАЯ ФОРМА ПОВЕРХНОСТИ. В произвольной точке
определяет направление на поверхности, имеем
Производная от
Малое смещение
Отсюда получаем, вычисляя скалярный квадрат
III.1. РЕГУЛЯРНАЯ ПОВЕРХНОСТЬ. На евклидовой плоскости
плоской области
Эти функции непрерывны, ввиду того, что отображение
Отображение
Задается поверхность векторной функцией
Поверхность Наложим на функцию (1) (2) Векторы
Поверхность, заданная векторной функцией с указанными условиями, называется регулярной класса
|
||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 655; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.006 с.) |
 выбрана некоторая область
выбрана некоторая область  , гомеоморфная прямоугольнику. Можно считать, что
, гомеоморфная прямоугольнику. Можно считать, что  ,
,  , т.е.
, т.е.  ,
,  и
и  , область
, область  . Плоскость
. Плоскость  , где
, где  евклидова метрика на
евклидова метрика на 
 , в котором точке
, в котором точке  из
из  , в
, в  . Отображение
. Отображение  является гомеоморфным - взаимно однозначным и взаимно непрерывным. В
является гомеоморфным - взаимно однозначным и взаимно непрерывным. В  . При изменении точки
. При изменении точки  в области
в области  в пространстве
в пространстве  ,
,  ,
,  точки
точки  ,
,  ,
,  ,
,  .
. ,
,  .
.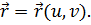
 составляют концы векторов
составляют концы векторов  , поэтому поверхность
, поэтому поверхность 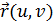 .
. условия:
условия: , т.е. существуют непрерывные частные производные этой функции до третьего порядка включительно;
, т.е. существуют непрерывные частные производные этой функции до третьего порядка включительно; ,
,  неколлинеарны в точках области
неколлинеарны в точках области  .
. - линии поверхности, это линии
- линии поверхности, это линии  ,
,  ;
; - линии
- линии  ,
,  .
. ; производные
; производные  ,
,  вычислены в точке
вычислены в точке  .
. ,
,  , то на поверхности
, то на поверхности  ,
, 
 выполняется
выполняется ,
, всякой линии поверхности
всякой линии поверхности  , проходящей через точку
, проходящей через точку  . Касательная прямая
. Касательная прямая  всякой кривой
всякой кривой  . Касательные всех линий поверхности
. Касательные всех линий поверхности  . #
. # и производные
и производные  .
. называется нормалью поверхности
называется нормалью поверхности  в точке
в точке  .
.
 .
. имеет вид
имеет вид .
. по кривой
по кривой  на поверхности вычисляется на основании равенств
на поверхности вычисляется на основании равенств .
. ,
, . (III.4.1)
. (III.4.1) ,
,  ,
,  . (III.4.2)
. (III.4.2) . (III.4.3)
. (III.4.3)


