
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Опр. Теплопередачи. Виды теп-и, ихкраткаяхар-ка. Осн-ыеопр-я, вел. Иих ед. Изм-я, характеризующиетепл. Процессы.Содержание книги
Поиск на нашем сайте
Теплопередача —физ. процесс передачи тепл. эн-и от более гор-го тела к более хол-ому либо непосредственно (при контакте), либо ч/з разделяющую перегородку из какого-либо м-ла Всего существует т ри простых (элементарных) вида передачи тепла:- Теплопроводность (явление теплообмена между частицами или элементами материальной среды, находящимися в непосредственном контакте);- Конвекция; - Тепловое излучение t–температура, мера кинет-ой эн-и атомов и молекулл в-ва, оС, К в теплотехнических расчетах применяется tн — температура наружного воздухаtв – температура внутреннего воздуха количество теплоты, Дж, кал, ккал, кВт·ч 1 ккал = 4,1868 кДж; 1 кВт·ч = 3 600 кДж Q–тепловойпоток– это к-во теплоты переносимое за единицу времени (т.е. это мощность), Дж/с, Вт q–плотностьтеплового потока(поверхностная) – тепловой поток, прох-ий ч/з единицу площади F поверхности теплообмена, Вт/м2 λ–коэффициент теплопроводности– кол-во тепла, переносимое в стационарном режиме за 1 с ч/з площадь 1 м2 плоской стенки из данного м-ла толщиной 1 м при разности температур на внешн. и внутр. пов-ти 1 оС (1 К) Вт/(м·К), Вт/(м·оС) c – удельная теплоемкость – отнош. подведенного к телу кол-ва теплоты к произв-ю массы данного тела на изм-ие его температуры, Дж/(кг·К),Дж/(кг·оС), С – теплоемкость тела – кол-во теплоты, необх. для нагрева тела на 1 оС (1 К),Дж/К), Дж/оС Теплоемкость – это св-во м-ла поглощать (аккумулировать) тепло при нагревании и выделять его при охлаждении К-во теплоты, которое необходимо для повышения температуры материала на Δ t 9.Ур-етеплопров.Фурье для одномерного случая встац.реж.Коэфф.теплопров.: физ.смысл, ед.изм.,осн.особенности (зав-стьотразл.факторов). Закон теплопроводности Фурье В установившемся режиме поток энергии, передающейся посредством теплопроводности, пропорционален градиенту температуры: q=-λgrad(T) где q — вектор потока тепла — количество энергии, проходящей в единицу времени через единицу площади, перпендикулярной каждой оси, λ— коэффициент теплопроводности (иногда называемый просто теплопроводностью), T — температура. Минус в правой части показывает, что тепловой поток направлен противоположно вектору grad T (то есть в сторону скорейшего убывания температуры). Это выражение известно как закон теплопроводности Фурье. В интегральной форме это же выражение запишется так (если речь идёт о стационарном потоке тепла от одной грани параллелепипеда к другой): где P — полная мощность тепловых потерь, S — площадь сечения параллелепипеда, ΔT — перепад температур граней, h — длина параллелепипеда, то есть расстояние между гранями. Коэффициент теплопроводности измеряется в Вт/(м·K). Коэффициент теплопроводности вакуума почти ноль (тем ближе к нулю, чем глубже вакуум). Это связано с низкой концентрацией в вакууме материальных частиц, способных переносить тепло. Тем не менее тепло в вакууме передаётся с помощью излучения. Поэтому для уменьшения теплопотери стенки термоса делают двойными, серебрят (такая поверхность хуже излучает и лучше отражает), а воздух между ними откачивают. Примеры теплопроводности:алмаз 1001-2600, серебро430,золото320, кирпич строительный 0,2-0,7, пенобетон 0,14-0,3, вакуум 0
Уравнение диффузии или уравнение теплопроводности представляет собой частный вид диф-ого ур-я в частных производных. Бывает нестационарным и стационарным. В случае одномерного диффузионного процесса с коэффициентом теплопроводности D уравнение имеет вид:
где с(x,t)— концентрация диффундирующего вещества, a В трёхмерном случае уравнение приобретает вид:
где
а при постоянном D приобретает вид:
N-мерный случай n-мерный случай — прямое обобщение приведенного выше, только под оператором набла, градиентом и дивергенцией, а также под оператором Лапласа надо понимать n-мерные версии соответствующих операторов:
Это касается и двумерного случая n = 2.
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 253; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.011 с.) |

 10. Диф-ое ур-ие теплопроводности для стац-го инест-ого режима: а) одномерное; б) двумерное; в) трехмерное. Темп-ное поле: пр-ры одн-ных и неодн-ных темп-ных полей. Участки ОК, где формируются слож-ныетемп-ные поля.
10. Диф-ое ур-ие теплопроводности для стац-го инест-ого режима: а) одномерное; б) двумерное; в) трехмерное. Темп-ное поле: пр-ры одн-ных и неодн-ных темп-ных полей. Участки ОК, где формируются слож-ныетемп-ные поля. При постоянном D приобретает вид:
При постоянном D приобретает вид: 
 — функция, описывающая источники вещества (тепла).
— функция, описывающая источники вещества (тепла).
 — оператор набла, а
— оператор набла, а 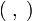 — скалярное произведение. Ур-ние также может быть записано как
— скалярное произведение. Ур-ние также может быть записано как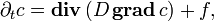
 где
где  — оператор Лапласа.
— оператор Лапласа.




