Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статические и динамические объекты программ.Содержание книги
Поиск на нашем сайте
Вектор. Функциональная спецификация. Логическое описание и физическое представление. Вектор является последовательностью переменной длины, и время доступа к элементам этой последовательности постоянно и не зависит от длины последовательности. Количество элементов вектора не фиксировано и всегда может быть изменено. Вектор с 0 компонент называется пустым (но аналогии с пустым файлом). В математике операции, такие как сложение и скалярное произведение, можно производить только с векторами равной размерности (длины). Поэтому длина является важной характеристикой вектора. Обозначим через In множество допустимых индексов вектора, I = 0,..., n-1. Мощность этого множества есть ни что иное как длина вектора. В качестве индекса первого элемента берется 0, т. к. это удобно для реализации вектора в ЭВМ. Для доступа к компоненте вектора необходимо прибавить к адресу блока размер одной компоненты, умноженной на ее индекс. Если индексация ведется не с 0, то дополнительно необходимо провести сложение индекса с некоторым числом, что замедляет доступ. Описание самого вектора: Определение его длины: По окончанию работы удаление вектора и возврат памяти ОС: typedef struct { T* data; int size; } Vector;
void Create(Vector* v. int sz) { v—>size = sz; v—>data = malloc(sizeof(T) * v—>size)); }
void Destroy (Vector* v) { v—>size — 0; free (v— > data); Стек. Физическое представление (динамические объекты). Стек представляется как линейный список, в котором включение элементов всегда производятся в начала списка, а исключение - также из начала. Для представления его нам достаточно иметь один указатель - top, который всегда указывает на последний записанный в стек элемент. В исходном состоянии (при пустом стеке) указатель top - пустой. Процедуры StackPush и StackPop сводятся к включению и исключению элемента в начало списка. Обратите внимание, что при включении элемента для него выделяется память, а при исключении - освобождается. Описание элементов стека аналогично описанию элементов линейного однонаправленного списка. Поэтому объявим стек через объявление линейного однонаправленного списка: struct Stack { Single_List *Top;//вершина стека }; .......... Stack *Top_Stack;//указатель на вершину стека
Основные операции, производимые со стеком:
создание стека; печать (просмотр) стека; добавление элемента в вершину стека; извлечение элемента из вершины стека; проверка пустоты стека; очистка стека. 7. Очередь. Функциональная спецификация. Очередь — это структура с одной читающей головкой и одной записывающей головкой, последовательным доступом и неразрушающей записью [72]. Точнее, очередью называется упорядоченное множество с переменным (возможно, нулевым) числом элементов, на котором определены следующие операции: 1.Постановка в очередь нового элемента; 2.Проверка пустоты очереди; 3.Просмотр 1го элемента, если он есть; 4. Извлечение из очереди ее 1го элемента, если очередь не пуста. Очереди применяют к 2м классам задач: Для моделирования реальных очередей; Решение собственных задач информатики, в частности в области операционных систем ЭВМ. Количество компонент очереди называется ее длиной. Однако длина очереди в определении не фиксируется и может быть вычислена «вручную» последовательным перебором всех се компонент. То есть это неэлементарная составная операция. Компонента очереди может иметь любой тип, простой или составной. Тип QT (очередь объектов типа Т) характеризуется следующими операциями: 0 -> QT QT -> boolean QT xT->QT QT ->QT QT -> T QT -> N QT -> 0 1. Перечисленные операции имеют след. св-ва при 1. ПУСТО(СОЗДАТЬ) - true СОЗДАТЬ всегда порождает пустую очередь; 2. ПУСТО(В ОЧЕРЕДЬ (q,t)) = false 3. ПЕРВЫЙ (В ОЧЕР Е Д Ь (С О 3 Д АТЬ, £)) - t. Внесенный в пустую очередь элемент всегда становится ее первым элементом. 4. Последовательность действий: Заносящая во вновь созданную пустую очередь сначала элемент t1, а зачем элемент t2, а затем извлекающая из нее 2 элемента сохраняет их порядок. Стек. Логическое описание. Самый свежий элемент стека, т. е. последний введенный и еще не уничтоженный играет особую роль; именно его можно рассмотреть или уничтожить. Этот элемент называется верхушкой стека. Оставшуюся часть можно назвать телом стека и оно само является, но существу, стеком; если снять со стека верхушку, то тело превращается в сток. Таким образом, стек, как и очередь, является рекурсивной структурой данных и может быть описан рекурсивно как конкатенация элемента типа Т и некоторого стека s типа SТ.Для обеспечения эффективной вычислимости необходим терминатор, ограничивающий глубину рекурсии описания, роль которого, как в файлах и очередях, играет пустой стек:
type СТЕК-Т = (ПУСТО | НЕПУСТОЙСТЕК) type НЕПУСТОЙСТЕК = (верхушка: Т; тело: СТЕК-Т) const int POOL_SIZE-100 Заметим, что рекурсивность описания может быть не только по глубине стека, но и по сложности типа его компонент Т: этот тип может быть произвольным, в том числе и рекурсивным, и даже стеком... 13 Стек. Физическое представление (массив). Идеальной структурой представления для стека должен быть файл. Действительно, добавление элементов происходит только в конец файла, однако при удалении последнего элемента придется два раза переписывать весь файл, причем с подсчетом элементов. Это главный недостаток файла – для удаления компоненты требуется слишком много действий. С другой стороны время удаления элементов из файла не зависит ни от положения этого элемента в файле, ни от количества удаляемых элементов – это плюс! Реализация стека с помощью массива позволяет уравнять время выполнения действий по добавлению и удалению элемента. Нужно всего лишь хранить в отдельной переменной длину последовательности и увеличивать ее или уменьшать соответственно при добавлении и удалении. Единственный недостаток такого представления – недостаток самого массива – ограниченный размер, приводящий к переполнению стека Использование динамических структур полностью решает эту проблему. В этом случае при добавлении и удалении элемента модифицируется только ссылка на начало цепочки динамических объектов, что снижает до минимума количество используемых для действия операторов. При этом размер стека почти неограничен. Начало последовательности называется дном стека, конец последовательности, в который производится добавление элементов и их исключение - вершиной стека. Переменная, которая указывает на последний элемент последовательности в вершине стека - указатель стека. Операция добавления нового элемента (запись в стек) имеет общепринятое название Push (погрузить), операция исключения - Pop (звук выстрела). Операции Push и Pop являются безадресными в том смысле, что для их выполнения никакой дополнительной информации о месте размещения элементов не требуется (для этого достаточно указателя стека)
15 Линейный список. Функциональная спецификация. Линейный список — это представление в ЭВМ конечного упорядоченного динамического множества элементов типа Т. Точнее, это не множество, а мультимножество, т. к. в последовательности могут находиться элементы с одинаковыми значениями. Элементы этого множества линейно упорядочены, но порядок определяется не номерами (индексами), как в массиве, а относительным расположением элементов. Отношений порядка па этом множестве может быть не одно, а два, и тогда мы имеем дело с двусвязными (двусторонними или симметричными) списками. Для закольцевания списка необходимо доопределить в качестве следующего за. последним первый элемент списка, а в качестве предыдущего первому элементу — последний (голова указывает на хвост, а хвост на голову). Таким образом отношения порядка (предыдущий и /или следующий) становятся определенными для всех смежных (с точностью до закольцевания) пар элементов списка. Список обозначается простым перечислением элементов в заданном порядке в круглых скобках через запятую. Например, список l из пяти элементов типа T выглядит так: l = (t1, t2, t3, t4, t5)
Полная функциональная спецификация двусвязного линейного списка LT объектов типа T достаточно длинна: СОЗДАТЬ: 0 -> LT ПУСТО: LT -> boolean ДЛИНА: LT ->N ПЕРВЫЙ: LT -> T ПОСЛЕДНИЙ: LT -> T СЛЕДУЮЩИЙ: LT x T -> T ПРЕДЫДУЩИЙ: LT x T -> T ВСТАВКА: LT x T x T -> LT УДАЛЕНИЕ: LT x T -> LT УНИЧТОЖИТЬ: LT -> 0.
Свойства: ПУСТО (СОЗДАТЬ) - true ПУСТО (ВСТАВКА (l, t, t) — false ПРЕДЫДУЩИЙ(СЛЕДУЮЩИЙ(t)) = t СЛЕДУЮЩИЙ(11РЕДЫДУЩИЙ(t)) = t l:— СОЗДАТЬ l:— ВСТАВКА (l, t2, t2) l: ВСТАВКА(l, t2, t1) ПЕРВЫЙ (l) = t1 ПОСЛЕДНИЙ (l) = t2 В левой части спецификации операции ВСТАВКА находится декартово произведение трех множеств: всевозможных списков, в которые должна быть проведена вставка, всех элементовПЕРЕДкоторыми необходимо ее произвести и различных вставляемых элементов. 16 Линейный список. Логическое описание. В отличие от очередей и стеков списковые структуры, хотя и не входят в стандартные языки программирования, но хорошо реализованы в альтернативных достаточно распространенных языках Лисп и Пролог. Более того, в языке Лисп это основная структура. Рассмотрим сначала как списки реализованы в Прологе. По определению, пустой список является списком, он обозначается символом [ ]. Функтор «.» (точка) образует новый список путем добавления нового элемента в начало исходного списка. Так список (t1, t2, t3, t4, t5) может быть записан на Прологе как: .(t1,.(t2,.(t3,.(t4,.(t5, []))))) Логическое описание списков на Прологе базируется на встроенном предикате отделения головы списка «|» и реализованных на самом Прологе предикатах (программных единицах этого языка), более или менее соответствующих вышеприведенной функциональной спецификации: проверка членства элемента или подсписка в заданном списке, вычисление длины, конкатенация, генерация перестановок элементов списка. Остальное может быть легко дописано на Прологе. Примеры: [Tl, Т2, T3 | Tail] * Отделение от списка трех первых элементов. В результате переменные Tl, Т2 и ТЗ получают значения, первых трех элементов списка, а 'Tail становится, остатком списка */ % Определение длин ы производится, рекурсивно length([], О). length([_| Tail ], N):- length(Tail, N1), N is N1 + 1. Деревья. Двоичные деревья. Пусть Т – некоторый тип данных. Деревом типа Т называется структура, образованная элементом типа Т (корнем) и конечным (возможно пустым) множеством с переменным числом элементов – деревьев типа Т (поддеревьев) {не пустое} {дерево с нулевым разветвлением – линейная структура}
{для описания взаимного расположения элементов взята терминология из генеалогичекого дерева (отец и сын; потомок и предок; НО дочерняя вершина); сыновья одного дерева – братья} Приведём определения, относящиеся к дереву: а) элементы типа Т, входящие в дерево называют узлами (вершинами) б) число поддеревьев данного узла называют его степенью в) узел, не имеющий поддеревьев, называют листом (концевым узлом) г) уровень в дереве определяется рекурсивно: уровень корня каждого поддерева данного узла на “1” больше уровня донного узла; уровень корня всего дерева = 1. д) уровень дерева – макс. Уровень его вершин. Если порядок сыновей существенен, то сыновей упорядочивают “по старшенству” (подобно очереди), т.е. чем больше номер, тем дальше от предка. Определённые таким образом деревья называют деревьями общего вида. Двоичное (бинарное) дерево – конечное множество узлов, которое или пусто, или состоит из корня и 2х непересекающихся поддеревьев (левое и правое) {может быть пустым} (Пример:схема спортивного турнира) Предком для узла x называется узел дерева, из которого существует путь в узел x. Потомком узла x называется узел дерева, в который существует путь (по стрелкам) из узла x. Родителем для узла x называется узел дерева, из которого существует непосредственная дуга в узел x. Сыном узла x называется узел дерева, в который существует непосредственная дуга из узла x. Уровнем узла x называется длина пути (количество дуг) от корня к данному узлу. Листом дерева называется узел, не имеющий потомков. Внутренней вершиной называется узел, имеющий потомков. Высотой дерева называется максимальный уровень листа дерева. Упорядоченным деревом называется дерево, все вершины которого упорядочены (то есть имеет значение последовательность перечисления потомков каждого узла 23 Двоичное дерево. Функциональная спецификация Пусть BTt -двоичное дерево компонент типа T. Он характеризуется следующими операциями: а) создать (всегда создаётся пустое дерево) б) проверка на пустоту в) построить дерево (из корня и 2х поддеревьев) г) получение корня д) получение левого/правого поддеревьев е) уничтожение дерева Возможные операции над деревьями: а) чтение данных из узла б) создание дерева, состоящего из одного корня в) построение дерева из заданных корня и поддеревьев г) присоединение нового поддерева к узлу д) замена поддерева на новое е) удаление поддерева ё) получение узла, следующего за данным в определённом порядке Деревья выражений Деревья выражений – деревья, в узлах которых стоят элементы выражения (+, _, *, /, a = const, x!= const). при прямом обходе получаем префиксную (польскую) форму: * + a / bc – d * ef (КЛП – Левый-Корень-Правый) при обратном обходе получаем инфиксную (обычную) форму без скобок: a + b / c * d – e * f (ЛКП) при концовом обходе получаем постфиксную (обратную польскую) форму: abc / + def * - *( ЛПК) Пример1:Выражение (1+2)*4+3 в ОПН может быть записано так: 1 2 + 4 × 3 + Вычисление производится следующим образом (указано состояние стека после выполнения операции):
Ввод Операция Стек 1 поместить в стек 1 2 поместить в стек 1, 2 + сложение 3 4 поместить в стек 3, 4 * умножение 12 3 поместить в стек 12, 3 + сложение 15 Результат: 15, в конце вычислений находится на вершине стека. Пример2: для вычисления деревья выражений можно применить алгоритм Дейкстры основанный на применении стеков с приоритетами и польской записью:
30 Деревья поиска. Дерево поиска – это такое дерево, для каждого узла t которого выполняются следующие условия: 1) ключи всех узлов в левом поддереве меньше значения t 2) ключи всех узлов в правом поддереве больше значения t. Двоичные деревья часто употребляются для представления множеств данных, элементы которых должны быть найдены по некоторому ключу (нулю данных). В дереве легко и быстро найти элемент с заданным ключом: начиная от корня, двигаемся к левому или правому поддереву на основании лишь сравнения с ключом текущей вершины. По построению дерева поиска, переходя к одному из поддеревьев, мы автоматически исключаем другое поддерево с остальными узлами. Далее таким делением и исключением мы доходим до исключения подавляющего большинства вершин и нахождения нужных. Дерево поиска может быть использовано для упорядочивания данных. Для этого надо разместить эти данные в дереве поиска, а потом составить в результате его обхода упорядоченную последовательность. Но для решения этой задачи обычное дерево поиска не подходит: оно не допускает вхождения равнозначных элементов. Поэтому всякий новый элемент теперь должен быть включён в дерево. Для этого случай х = р^.key необходимо рассматривать вместе с одним из других. Если его объединить с х > р^.кеу, то порядок следования элементов с одинаковыми ключами совпадёт с хронологией их поступления в дерево. Возможность сочетания поиска и упорядочивания растущего множества данных, предоставляемая деревом поиска с включениями, даёт новое качество по сравнению с хранением данных как в списках, так и в массивах. Например, этим способом можно эффективно решить задачу составления таблицы перекрёстных ссылок слов текста.
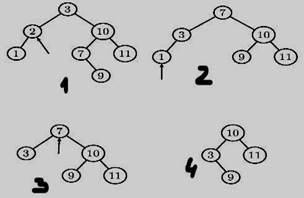
31 Сбалансированные деревья поиска. Т.к. введение новой вершины в идеально сбалансированное дерево его разбалансирует, то решили делать балансировку после вставки. AVL-дерево – то дерево, высота поддеревьев каждой из вершин которого отличается не более, чем на единицу. (идеально сбалансированное дерево является AVL-деревом)В AVL-дереве можно найти искомую вершину, добавить новую или удалить старую. Схема алгоритма включения в сбалансированное дерево такова: 1. поиск элемента в дереве; 2. включение новой вершины и определение результирующего показателя сбалансированности; 3. отход по пути поиска с проверкой показателя сбалансированности для каждой проходимой вершины, балансируя в необходимых случаях соответствующие поддеревья. Сложность балансировки оправдана тогда, когда поиск данных происходит значительно чаще¸ чем вставка. Двудетные вершины дерева обрабатываются путем замены самой правой вершины из левого поддерева. Удаление элементов выглядит так: 32 Простые методы поиска. Линейный поиск – последовательный просмотр массива как списка (цикл). Поиск происходит за O(N). Индексация начинается с 0. Ускорить поиск можно с помощью барьерного элемента. Его следует поместить в N+1 -ый элемент массива. Этот метод поиска единственный для структур данных со строго последовательным доступом. int function LinearSearch (Array A, int L, int R, int Key); Begin for X = L to R do if A[X] = Key then Return X Таблицы с прямым доступом. В 2х словах: ускорение работы с таблицей за счёт хеширования (перевода ключей элементов из литерной (символьной) формы в число, которое является указателем в памяти на этот элемент). {ведь обращение к элементу (чтение, запись, удаление) в конечном итоге есть обращение к памяти, так почему бы не начать сразу обращаться к памяти, пропуская сравнения ключей и всякое остальное} {для такого финта ушами нужно поместить таблицу с массив (доступ за постоянное время)} Для этого перевода нужна хеш-функция (отображение H ключей элементов в адреса памяти). Простейший пример хеш-функции: функция получения числового кода литера (если литеров несколько, то можно воспользоваться схемой Горнера: А = б + (i – 1) * sizeof(T), где б – адрес начала массива, i – индекс компоненты вектора, отсчитываемый от “1”, sizeof(T) – размер компоненты вектора). Проблема в том, что разные ключи могут соответствовать одному адресу. Такие случаи называются коллизиями. На такой случай нужно предусмотреть операцию рехеширования – переадресация, в случае занятости адреса (запись нового элемента) или в случая, когда по данному адресу находится элемент с другим ключом (чтение).{2 способа: организовать список строк с идентичным первичным ключом H(k) (этот список может расположить где душе угодно, но такой способ вызовет увеличение расхода памяти); или, при занятости данной ячейки памяти, “впихнуть” наш элемент куда-нибудь рядом} Достоинства таблицы с прямым доступом (хеш-таблицы) в том, что при линейных сложностях операций хеширования и рехеширования можно обрабатывать таблицу (читать, искать, добавлять новый элемент и удалять старые) за постоянное время. Недостаток – нельзя напечатать так быстро заполненную таблицу в упорядоченном виде, да ещё и сохраняя естественный хронологический порядок равнозначных элементов (нужна сортировка → что было до хеша). 38 Алгоритмы сортировки. Сортировка называется устойчивым (стабильным), если в процессе сортировки относительное расположение элементов с равными ключами не изменилось. Характеристики методов сортировки Время — основной параметр, характеризующий быстродействие алгоритма. Называется также вычислительной сложностью. Для упорядочения важны худшее, среднее и лучшее поведение алгоритма в терминах размера списка (n). Для типичного алгоритма хорошее поведение — это O(nlogn) и плохое поведение — это O(n²). Идеальное поведение для упорядочения — O(n). Память — ряд алгоритмов требует выделения дополнительной памяти под временное хранение данных. Устойчивость (stability) — устойчивая сортировка не меняет взаимного расположения равных элементов. Естественность поведения — эффективность метода при обработке уже упорядоченных, или частично упорядоченных данных. Алгоритм ведёт себя естественно, если учитывает эту характеристику входной последовательности и работает лучше. Использование операции сравнения. Алгоритмы, использующие для сортировки сравнение элементов между собой, называются основанными на сравнениях. Внутренняя сортировка оперирует с массивами, целиком помещающимися в оперативной памяти с произвольным доступом к любой ячейке. Данные обычно упорядочиваются на том же месте, без дополнительных затрат. В современных архитектурах персональных компьютеров широко применяется подкачка и кэширование памяти. Алгоритм сортировки должен хорошо сочетаться с применяемыми алгоритмами кэширования и подкачки. Внешняя сортировка оперирует с запоминающими устройствами большого объёма, но с доступом не произвольным, а последовательным (упорядочение файлов). Категория сортировок входящие в раздел “внутренние” имеют прямые методы сортировок. Сортировка вставкой (устойчивая). Вставка элемента в на нужную позицию в уже отсортированном массиве. Сортировка выборокой (не устойчивая). 1-ый элемент меняется местами с минимальным, далее 2-ой так же.. Пузырьковая сортировка. 1-ый элемент сравнивается с соседним, если >, то меняются местами, если <, то берется тот элемент с кем происходило сравнение и сравнивают его, так пока не дойдем до конца. В 1-ой итерации всегда всплывет максимальный элемент. Сортировка Шелла. Выбирается интервал d, через которые будут сравниваться элементы в первый проход, к примеру 5, после полного прохода, берется новый интервал 3 и опять проход и так далее. Турнирная сортировка.
39 Сортировка вставкой. Преимущества данного алгоритма: 1)эффективен на небольших наборах данных, на наборах данных до десятков элементов может оказаться лучшим; 2)эффективен на наборах данных, которые уже частично отсортированы; 3)это устойчивый алгоритм сортировки (не меняет порядок элементов, которые уже отсортированы); 4)может сортировать список по мере его получения; 5)использует 0(1) временной памяти, включая стек. Минусом же является высокая сложность алгоритма: 0(n^2). На каждом шаге алгоритма мы выбираем один из элементов входных данных и вставляем его на нужную позицию в уже отсортированном списке, до тех пор, пока набор входных данных не будет исчерпан Метод выбора очередного элемента из исходного массива произволен; может использоваться практически любой алгоритм выбора. Обычно (и с целью получения устойчивого алгоритма сортировки), элементы вставляются по порядку их появления во входном массиве. Приведенный ниже алгоритм использует именно эту стратегию выбора: у нас есть колода на столе и отсортированный веер карт в руке; берём из колоды карту и вставляем в веере в нужное место; и так до того, пока карты не закончатся. {т.е. у нас есть 2 части массива: отсортированная и не отсортированная} {массив из одного или нуля элементов отсортирован!}
сложность O(n^2) Вход: массив A, состоящий из элементов A[1], A[2],..., A[n]
for i = 2, 3,..., n: key:= A[i] j:= i - 1 while j > 0 and A[j] > key: A[j + 1]: = A[j] j:= j - 1 A[j + 1]: = key 40 Сортировка выборкой. Алгоритм сортировки может быть реализован и как устойчивый и как неустойчивый. На массиве из п элементов имеет время выполнения в худшем, среднем и лучшем случае О(n^2), предполагая что сравнения делаются за постоянное время. Шаги алгоритма: 1.находим номер минимального значения в текущем списке; 2.(только 8 устойчивых реализациях) если значения элементов неравны, то; 3.производим обмен этого значения со значением первой не отсортированной позиции; 4.теперь сортируем хвост списка, исключив из рассмотрения уже отсортированные элементы. Пример: void selectSort(T a[], long size) { long i, j, k; T x; for(i=0; i < size; i++) { // i - номер текущего шага k=i; x=a[i]; for(j=i+1; j < size; j++) // цикл выбора наименьшего элемента if (a[j] < x) { k=j; x=a[j]; // k - индекс наименьшего элемента } a[k] = a[i]; a[i] = x; // меняем местами наименьший с a[i] } }
42 Сортировка Шелла. Первое улучшение алгоритма заключается в запоминании, производился и на данном проходе какой-либо обмен. Если нет - алгоритм заканчивает работу. Процесс улучшения можно продолжить, если запоминать не только сам факт обмена, но и индекс последнего обмена k. Действительно: все пары соседних элементов с индексами, меньшими k, уже расположены в нужном порядке. Дальнейшие проходы можно заканчивать на индексе k, вместо того чтобы двигаться до установленной заранее верхней границы i. Качественно другое улучшение алгоритма можно получить из следующего наблюдения. Хотя легкий пузырек снизу поднимется наверх за один проход, тяжелые пузырьки опускаются со минимальной скоростью: один шаг за итерацию. Так что массив 2 3 4 5 6 1 будет отсортирован за 1 проход, а сортировка последовательности 6 1 2 3 4 5 потребует 5 проходов. Чтобы избежать подобного эффекта, можно менять направление следующих один за другим проходов. Получившийся алгоритм иногда называют "шейкер-сортировкой". Выигрыш Шелла в том, что на каждом шаге либо сортируется мало элементов, либо они досортировываются. Недостатки – не устойчивость и сложны математический анализ (до сих пор не найдена универсальная последовательность шагов, дающая минимальную сложность). Сложность O (n ^ (1+б)), где б от “0” до “1”, что хуже, чем n * lnn Турнирные сортировки. В сортируемом множестве можно сравнить пары соседних элементов → из n/2 сравнений получаем меньшую по значению ключей половину (победители); также из получаем четверть и т.д., пока не получим один элемент. Результат – дерево выбора (турнирная таблица – двоичное дерево, в котором для каждого двудутного узла один из сыновей – он сам (победитель), а другой больше своего отца) (в корне – самый маленький элемент) Перевода в множество: а) возьмём корень и запишем его в множество б) спускаемся от победителя к призёрам по пути победителя, опустошая вершины в) поднимаясь по этому пути, выполняем перераспределение мест, как будто победителя из п.а не было (элемент, соревнующийся с пустым местом, автоматом переходит в следующий тур) г) теперь место победителя занял новый элемент; переходим к п.1 Достоинство – сложность всегда О(n * lnn). {для уменьшения расхода памяти необходимо применить пирамидольное улучшение традиционных древовидных сортировок (hi =<h2ihi =<h[2i+1]); в пирамиде нет повторов элементов сортируемого множества} Строительство пирамиды: 1) первоначально элемент помещается в вершину, i = 0 2) рассмотрим тройку элементов с индексами i, 2i, 2i+1 (узел и его дети) 3) выберем наименьший из п.2: если он на позиции i, элемент вставлен; ELSE обозначим позицию наименьшего буквой j, где j=j2i или j = 2i + 1, меняем местами элементы i и j 4) переходим к п.2
44 Сортировка Хоара. Быстрые сортировки – те, в которых осуществляются перестановки на большие расстояния. Алгоритм:. В методе Хоара первоначально выделяют базовый элемент, относительно которого ключи с большим весом перебрасываются вправо, а с меньшим влево. Базовый элемент сравнивается с противоположным элементом.. В качестве базового элемента очень удобно брать крайние элементы.. Рассмотрим пример: Дано множество {9,6,3,4,10,8,2,7}. Берем 9 в качестве базового элемента. Сравниваем 9 с противоположностоящим элементом, в данном случае это 7. 7 меньше, чем 9, следовательно, элементы меняются местами. >> {7,6,3,4,10,8,2,9}. Далее начинаем последовательно сравнивать элементы с 9, и менять их местами в зависимости от сравнения. {7,6,3,4,10,8,2,9} >> {7,6,3,4,10,8,2,9}>>{7,6,3,4,10,8,2,9}>> {7,6,3,4,9,8,2,10} - 9 и 10 меняем местами. >> {7,6,3,4,8,9,2,10} - 9 и 8 меняем местами. >> {7,6,3,4,8,2,9,10} - 2 и 9 меняем местами.. После такого перебрасывания элементов весь массив разбивается на два подмножетсва, разделенных элементом 9. >>{7,6,3,4,8,2} {10}. Далее по уже отработанному алгоритму сортируются эти подмножества. Подмножество из одного элемента естественно можно не сортировать.Выбираем в первом подмножестве базовый элемент 7. >>{7,6,3,4,8,2} >> {2,6,3,4,8,7}-меняем местами 2 и 7>>{2,6,3,4,8,7}>>{2,6,3,4,8,7}>>{2,6,3,4,8,7}>>{2,6,3,4,7,8}-меняем местами 7 и 8 Получили снова два подмножества: {2,6,3,4} {8}. Достоинства – легко распаралеливается, что полезно в нашь век многопроцессорных/ядерных/потоковых ЭВМ. (лучший случай - когда каждыё раз медиана выбирается зерном). Есть ещё и итеративное решение, в котором мы запоминаем границы подпоследовательностей, которые нужно отсортировать, но на практике оба варианта этого алгоритма занимают одинаковое время. Недостаток – плохо работает при малых n (в прочем, как и все усовершенствованные методы) 45 Сортировки слиянием Решения задачи сортировки: 1) последовательность а разбивается на 2 половины b и c 2) каждая из получившихся частей сортируется отдельно тем же самым алгоритмом 3) два упорядоченных массива половинного размера соединяются в один. 4) части b и c сливаются; при этом одиночные элементы из разных частей образуют упорядоченные пары в выходной последовательности, т.е. первым в ней оказывается меньший из 2х первых элементов 5) полученная последовательность более упорядочена чем изначальная и она снова подвергается разделению и слиянию; при этом упорядоченные пары переходят в четверки, те – в 8ки и т.д.. Пример(МОЙ!!): (40 47 10 38 80 20 01 50)→(40 47 10 38) (80 20 01 50) →(40 80 20 47 01 10 38 50) →(40 80 20 47)(01 10 38 50) →(01 10 40 80 20 38 47 50) →(01 10 40 80)(20 38 47 50) →(01 10 20 38 40 47 50 80) Обменные сортировки Алгоритм: 1) берём первый элемент. 2) сравниваем со следующим. 3) если следующий больше – наш оставляем на месте и берём следующий; ELSE меняем местами. 4) п.2, пока не дошли до конца (эффективнее держать номер начала отсортированной части). 5) п.1пока есть эементы. Улучшение – сортировка Шеёкер = 2пузырька, направленные в разные стороны (один тащит наименьтшие к началу, а другой – наибольшие к концу). Пример – труба, в которой находятся разные по плотности не смешиваемые жидкости: более лёгкие всплывут на поверхность, а более тяжёлые уйдут на дно. Прост в программирование, но сложность O(n^2) + один не удачно расположенный элемент будет “просачиваться” на своё место со скоростью 1 позиция за проход. emplate<class T> void bubbleSort(T a[], long size) { long i, j; T x; for(i=0; i < size; i++) { // i - номер прохода for(j = size-1; j>i; j--) { // внутренний цикл прохода if (a[j-1] > a[j]) { x=a[j-1]; a[j-1]=a[j]; a[j]=x; } } } }
55-56 Адресный тип. Реализация полиморфизма с помощью адресного типа на языке Си. Для обеспечения процессов разнотипной интерпретации памяти необходимо применение родовых типов. Родовые типы данных уже заложены в конструкцию универсальных ЭВМ, память которых представляет собой слова, предназначенные для хранения данных произвольных типов. Ослабляя ограничения строго типизированных языков, можно ввести родовой тип данных word, не предполагающий какого-либо особенного использования памяти, выделенной для его объектов. Для этого типа определены лишь операция присваивания и отношение равенства. Поскольку он внутримашинный, он непечатаемый и в нём нет констант, изображающих конкретные значения. Основное его применение – ослабление контроля типов при передаче параметров. Любой формальный параметр типа word считается совместимым с любым фактическим параметром, занимающим ровно одно слово в памяти ЭВМ. Более универсальный способ ослабления типового контроля – применение родовых (бестиповых) указателей. В соответствии с описанным выше типом word их можно ввести как указатели на word, распространяя типовую свободу word на мир ссылок и указателей. В Си бестиповый указатель может быть объявлен как void*. Фактически тип родового указателя вводит в обиход языка адреса соответствующей ЭВМ, единообразно ссылающиеся на данные любых типов, размещённые в ячейках её памяти. Поэтому он называется адресным типом. Он имеет множеством значений диапазон допустимых адресов ЭВМ (возможно, суженный до сегмента памяти в системах с защитой памяти). Объекты адресного типа совместимы по присваиванию и сравнению с любыми ссылочными переменными, а формальные переменные – с любыми ссылочными фактическими. Кроме того, адресный тип совместим с целым и к нему применимы некоторые арифметические операции, такие как сложение и вычитание. 57 -58 Процедурный тип данных. Реализация полиморфизма с помощью процедурного типа на языке. Проц.Тип д. – ещё одно средство реализации родовых модулей. Этот тип позволяет трактовать процедуры и функции как значения, которые можно присваивать переменным или передавать в качестве параметров другим подпрограммам. Фактически, процед. Тип данных представляет собой целый класс типов, отдельные типы которого есть множества глобально определённых процедур с идентичной спецификацией, включая и тип результата для функций. Константами процедурных типов являются имена глобальных процедур. Переменные процед. Типа принимают значения из соответствующего спецификации заголовка множества процедур. Разумеется, её можно и вызвать. Проц. Тип данных может играть адрес функции, поскольку в конечном счёте для её вызова его надо знать. Примечательно, что процед. Типы в раздельно компилируемых модулях делают эти модули родовыми по отношению к процедурам, а не к типам данных. Процедурный тип позволяет описывать более универсальные родовые модули с хранимыми процедурами, поскольку подстановка параметров процедурного типа (интегрируемой функции – в «функцию» интегрирования) существенно повышает параметризацию такого модуля. В Си и С++ просто предусмотрены указатели на функции (с возможностью приведения их к обобщённому указателю void*). 59 Наследование. Определять новый тип, наследующий те и только те атрибуты исходного типа, которые желательны. Пополнять перечни атрибутов нового типа по сравнению с атрибутами исходного типа (обогащение типов (возможность вводить дополнительные поля при объявле- нии производного типа) и виртуальные операции, заменяющие старые операции при действиях с обогащенными значениями, даже в старых программах). Гарантировать применимость сохраняемых операций исходного типа к объектам нового типа. Основные понятия и неформальные аксиомы наследования: —Отношение наследования между родителем и наследником — Атрибуты наследования — Накопление атрибутов у наследника по отношению к родителю — Типы объектов и экземпляры (объектов) определенных
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 564; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.72.181 (0.021 с.) |