Конгруэнтные процедуры генерации

Два целых числа а и b конгруэнтны (сравнимы) по модулю т, где т — целое число, тогда и только тогда, когда существует такое целое число k, что a-b=km, т. е. если разность a-b делится на т и если числа а и b дают одинаковые остатки от деления на абсолютную величину числа т.

Например, 20-8=3*4

4. Мультипликативный метод

Мультипликативный метод задает последовательность неотрицательных целых чисел { xi }, не превосходящих М, по формуле

xi+1= l xi (mod M).

Для машинной реализации наиболее удобна версия М = pg, где p - число цифр в системе счисления, принятой в ЭВМ, а g - число бит в машинном слове.

Смешанный метод

Позволяет вычислить последовательность неотрицательных целых чисел {Xi}, не превосходящих М, по формуле

Хi = lХi + m (mod M).

С вычислительной точки зрения смешанный метод генерации сложнее мультипликативного на одну операцию сложения, но при этом возможность выбора дополнительного параметра позволяет уменьшить возможную корреляцию получаемых чисел.

В настоящее время почти все пакеты прикладных программ универсальных ЭВМ для вычисления последовательностей равномерно распределенных случайных чисел основаны на конгруэнтной процедуре.

Проверка и улучшение качества последовательностей псевдослучайных чисел: проверка случайности, независимости, равномерности, характеристики качества генераторов, методы улучшения качества последовательностей.

n Методы проверки делятся на

§ тесты проверки «случайности» -основываются на статистических критериях согласия, из которых наиболее употребительным является критерий Пирсона (хи-квадрат).

§ тесты проверки равномерности – то же самое;

§ тесты проверки независимости -проводится на основе вычисления корреляционного момента (1-линейная, (0,в)-не линейная зависимость, 0 – нет зависимости).

Проверка равномерности

Данный тест строится на основе применения критерия согласия χ2 (Пирсона).

Если подсчитанное значение не попадает в доверительный интервал, то гипотезу о равномерном законе распределения случайной величины e следует отвергнуть.

Дополнительно можно подсчитать эмпирическое математическое ожидание и эмпирическую дисперсию

 

И соответственно

Гистограмма частот, являющаяся аналогом плотности распределения, строится следующим образом.

n Весь интервал (хmin, хmax) полученной выборки случайной величины разбивается на q равных промежутков длины h.

n Затем определяется число значений ni выборки, попавших в i-ый промежуток, после чего для каждого 1 £ i £ q строится прямоугольник с основанием на i-ом промежутке и высотой (ni /N)/h.

Можно использовать метод проверки по косвенным признакам. Суть его сводится к следующему.

Генерируемая последовательность разбивается на две последовательности

x1, x3,…,x2i-1;

x2, x4,…,x2i

Если выполняется условие

то фиксируется наступление некоторого события и в счетчик добавляется 1. После N/2 опытов в счетчике будет некоторое число k<N/2.

Геометрически данное условие означает, что точка (x2i-1,x2i) находится внутри четверти круга радиусом 1. Теоретически вероятность попадания этой точки в четверть круга p=S1/4круга/Sквадрата=π/4

Если числа последовательности равномерны, то в силу закона больших чисел при больших N относительная частота 2k/N π/4

 

Проверка случайностей

На практике обычно применяют тест проверки серий.

Тест проверки серий предусматривает разбиение случайных цифр в исследуемой последовательности на элементы двух родов - первого и второго.

Серией называется любой отрезок последовательности цифр, состоящий из следующих друг за другом элементов одного и того же рода.

В практике встречается разновидность теста проверки серий, когда к элементам серий первого рода относят цифры, меньшие 0.5, а к элементам серий второго рода - не меньшие 0.5.

Проверка независимости

Проверка независимости элементов последовательности может быть проведена путем введения в рассмотрение последовательности {yj}={xi+τ}, где τ – величина сдвига последовательностей.

 

Для оценки степени некоррелированности последовательности псевдослучайных чисел e1, e2, ¼,eN можно применять способ, заключающийся в определении коэффициента корреляции r(ei,i) между элементом ei последовательности и его номером i:

Если при заданном уровне значимости b коэффициент корреляции больше верхней границы доверительного интервала, то считается, что имеет место корреляционная связь между псевдослучайными числами. В противном случае можно принять гипотезу об их независимости

Качество генераторов характеризуется:

· Длина отрезка апериодичности L - последовательности псевдослучайных чисел {xi} есть наибольшее целое число L, такое, что при 0≤j<i≤L событие А{xi = xj} не имеет места (т.е. числа не повторяются).

· Длина периода Р

·

Методы улучшения качества последовательностей псевдослучайных чисел:

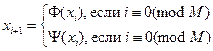n Использование рекуррентных формул порядка r>1 - Длина отрезка апериодичности у такой последовательности гораздо больше. Однако при этом возрастает сложность метода, при приводит к увеличению затрат машинного времени на получение чисел

n Метод возмущений -

 

В этом случае в основном используется формула xi+1= Φ (xi), и только когда i кратно М, последовательность возмущается, т.е. реализуется переход к формуле xi+1= Ψ (xi). Целое число М называется периодом возмущения.