
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Величины, характеризующие силовой энергетический трансформаторСодержание книги
Поиск на нашем сайте
Силовые энергетические трансформаторы бывают масляными и сухими. У масляных трансформаторов различают две части. 1) Активная часть – это сердечник с обмотками. 2) Бак с его элементами конструкции. Сухой трансформатор – это фактически сердечник с обмотками. Здесь мы будем иметь в виду только величины, относящиеся к активной части трансформатора, в ней осуществляется преобразование энергии. Энергия в установившихся режимах равна произведению мощности на время Э = Pt. Она не может быть собственной характеристикой трансформатора и вообще любого её преобразователя, так как её величина зависит от продолжительности времени работы t. Мощность же характеризует сам трансформатор (и вообще любой преобразователь) в различных режимах его работы. Размеры и массы сердечника и обмоток трансформатора определяются его номинальной мощностью Sн и номинальными напряжениями U1н и U2н. Исходной формулой при конструировании и проектировании трансформатора является формула трансформаторной ЭДС
Технически и экономически оптимальную конструкцию трансформатора ищут «играя» четырьмя величинами Bm, S, j, h. [Bm]=Тл, [S]=м2 [j]=А/мм2, [h]=м. Результатом этой «игры», то есть поиска, являются все основные величины (размеры и массы сердечника и обмоток, потери мощности в них, ток холостого хода и т.д.), характеризующие трансформатор. Для примера в приложении 1 приведены некоторые данные трансформаторов мощностью от 25 до 630 кВА с высшим напряжением 10, 6 кВ. Площадь сечения стержня S и его высота h характеризуют размеры сердечника, а магнитная индукция Bm в стержне и плотность тока в проводах обмоток j определяют электромагнитные нагрузки конструкции трансформатора. Другими словами, Bm и j определяют степень использования электротехнической стали сердечника и меди или алюминия обмоток. Что касается размеров обмоток (их диаметров и высоты), то они выражаются через размеры сердечника S и h и изоляционные расстояния одной обмотки от другой и обеих обмоток от стержней и ярем сердечника. Поиск технически и экономически оптимальной конструкции трансформатора при четырёх независимых переменных является весьма трудоёмким. Профессором П.М. Тихомировым разработан метод поиска, в котором независимой переменной является только одна величина – отношение средней длины витка двух обмоток lw к высоте обмоток hоб.
При величинах Площадь, занимаемая открытой подстанцией, получается меньшей если все виды её оборудования спроектированы высокими и узкими. Инженеры-пользователи техникой не занимаются её конструированием и проектированием. Их задачей является грамотное (квалифицированное) использование уже созданной техники. Такое использование силового энергетического трансформатора невозможно без знания величин, его характеризующих. На паспорте трансформатора и в справочной литературе приводятся только основные величины: 1. Номинальные данные Sн, U1н, U2н, I1н, I2н, cosφн, ηн, схема и группа соединения обмоток; 2. Данные режима холостого хода P0 и I0% 3. Данные режима короткого замыкания Pк и Uк% при условии I1 = I1н, I2 = I2н. Все остальные величины и зависимости между ними получаются путем расчета. Следует заметить, что величина cosφн фактически характеризует не сам трансформатор, а его нагрузку, то есть cosφн = cosφнг, и приводится на паспорте для указания на то, при каком значении cosφнг вычислен номинальный КПД ηн. Все остальные перечисленные величины характеризуют сам трансформатор. Так как под номинальными напряжениями U1н, U2н понимают линейные напряжения (напряжения между линейными проводами схем звезда, треугольник, зигзаг), а под номинальными токами I1н, I2н - линейные токи (токи в линейных проводах схем звезда, треугольник, зигзаг), то фазные напряжения (напряжения на зажимах обмоток фаз) и фазные токи (токи в обмотках фаз) подлежат вычислению. Номинальная мощность трансформатора Sн выражается через линейные вторичные величины U2н и I2н и
Откуда
В расчетной практике номинальную мощность Sн выражают и через линейные первичные величины
Откуда
Погрешность такого допущения при значениях cosφнг, встречающихся в условиях эксплуатации, и токе холостого хода I0 ≤ 3%, не превышает 1%. Для вычисления фазных напряжений и токов используют соотношения: · В схеме Y · В схеме Δ · В схеме зигзаг Z Схема зигзаг является последовательной как и схема звезда, поэтому ток в линейном проводе является и током в фазе обмотки. В схеме зигзаг с нулем номинальные фазные напряжения равны 231 В, а линейные 400 В, соответственно
Номинальные данные трансформатора – это данные на которые он спроектирован. В условиях эксплуатации трансформатора потребительского ТП его нагрузка изменяется, соответственно изменяются: токи I1 и I2, потери мощности ΔPт, КПД η, вторичное напряжение U2. Свойства трансформатора при изменяющейся нагрузке определяются зависимостями ΔPт, η, U2 от коэффициента его загрузки по току:
ΔPт=f(βI), η=f(βI), U2=f(βI)., (15.) Кроме этих трех зависимостей (трех характеристик) в расчетной практике используется еще зависимость от коэффициента βI не самого вторичного напряжения U2, а величины его изменения ΔU2 = U2н – U2. Для удобства пользования ΔU2 выражают в относительных единицах или в %
Для зависимости
в которой
а
Откуда записывается формула для Текущая величина фазного напряжения U2ф получается из формулы (16) для
Это первый простой способ нахождения текущей величины U2 при изменяющейся нагрузке. Так как
Это уравнение прямой линии внешней характеристики трансформатора
где Прямая линия внешней характеристики строится по двум точкам
Рисунок 3. Внешние характеристики трансформатора при двух значениях cosφНГ Потери мощности в трансформаторе складываются из потерь холостого хода Р0, фактически равных потерям в стали сердечника, и потерь в обмотках, пропорциональных
КПД трансформатора
где Р2 – активная мощность, снимаемая с зажимов вторичной обмотки. При расчете КПД её вычисляют по приближенной формуле
Тогда
Ток холостого хода I0 и напряжение короткого замыкания Uк задаются в %. В именованные единицы они переводятся по формулам:
Чтобы получить Uк с зажимов первичной обмотки, надо подставить 7. Соотношение между коэффициентом загрузки по мощности
Или, используя формулу косинуса разности углов, получим
где
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 422; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

 , (4.)
, (4.) , (5.)
, (5.) , не значительно отличающихся от единицы, активная часть трансформатора получается высокой, но небольшой по ширине и трансформатор в целом получается высоким но узким. При величинах
, не значительно отличающихся от единицы, активная часть трансформатора получается высокой, но небольшой по ширине и трансформатор в целом получается высоким но узким. При величинах 
 , (6.)
, (6.) , (7.)
, (7.)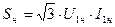 , (8.)
, (8.) , (9.)
, (9.) ,
,  ,
,  , (10.)
, (10.) ,
,  ,
,  , (11.)
, (11.) , (14.)
, (14.) , (16.)
, (16.) , (17.)
, (17.) известны разные приближенные формулы. Наиболее удобной для практических расчетов является формула
известны разные приближенные формулы. Наиболее удобной для практических расчетов является формула , (18.)
, (18.) ,
, задается характером нагрузки, т.е. величиной cosφнг. Формула для
задается характером нагрузки, т.е. величиной cosφнг. Формула для  получена из треугольника мощностей Sк, Pк, Qк короткого замыкания при I1=I1н
получена из треугольника мощностей Sк, Pк, Qк короткого замыкания при I1=I1н , (19.)
, (19.)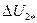
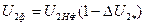 , (20.)
, (20.) , то и
, то и  . Зависимость
. Зависимость  при заданной величине
при заданной величине  , (21.)
, (21.) . В режиме холостого хода I2=0,
. В режиме холостого хода I2=0,  ,
,  . При номинальном токе нагрузки
. При номинальном токе нагрузки 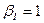 , а
, а , (22.)
, (22.) - вторичное напряжение при номинальном токе нагрузки (
- вторичное напряжение при номинальном токе нагрузки ( ,
, 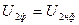
 ,
, 


 , (23.)
, (23.)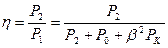 , (24.)
, (24.)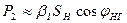 , (25.)
, (25.) , (26.)
, (26.)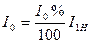 , (27.)
, (27.) , (28.)
, (28.) , с зажимов вторичной -
, с зажимов вторичной -  .
. и коэффициентом загрузки по току
и коэффициентом загрузки по току 
 , (29.)
, (29.) , (30.)
, (30.) , (31.)
, (31.) , (32.)
, (32.) , (33.)
, (33.) ,, (34.)
,, (34.) ,
, 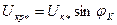
 ,
,  , (35.)
, (35.)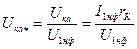 ,
,  , (36.)
, (36.)


