
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показатель и система показателей. Принципы формирования систем показателей разного вида.Содержание книги
Поиск на нашем сайте Технико-экономические показатели — инструменты хозяйственного руководства, отражающие отдельные стороны экономических процессов и явлений. Используя систему показателей, управляющая система планомерно воздействует на ход экономических процессов, контролирует их и создает условия для наиболее полной реализации требований, выдвигаемых перед объектом управления. Виды средних величин. Правило мажорантности средних. Важнейшие свойства арифметической средней и их использование в статистической практике. Средней величиной называется статистический показатель, который дает обобщенную характеристику варьирующего признака однородных единиц совокупности. Виды средних величин Средние величины делятся на два больших класса: степенные средние и структурные средние Степенные средние: § Арифметическая § Гармоническая § Геометрическая § Квадратическая Структурные средние: § Мода § Медиана Важнейшими условиями (принципами) для правильного вычисления и использования средних величин является следующие: 1. В каждом конкретном случае необходимо исходить из качественного содержания осредняемого признака, учитывать взаимосвязь изучаемых признаков и имеющиеся для расчета данные. 2. Индивидуальные значения, из которых вычисляются средние, должны относиться к однородной совокупности, а число их должно быть значительным. Показатели структуры, статистическая оценка однородности структуры (коэффициенты Лоренца и Джини). Коэффициент Джини — статистический показатель степени расслоения общества данной страны или региона по отношению к какому-либо изучаемому признаку. Коэффициент Джини изменяется от 0 до 1. Чем ближе его значение к нулю, тем более равномерно распределён показатель. Иногда используется процентное представление этого коэффициента, называемое индексом Джини. Иногда коэффициент Джини (как и кривую Лоренца) используют также и для выявления уровня неравенства по накопленному богатству, однако в таком случае необходимым условием становится неотрицательность чистых активов домохозяйства. 45.Показатели различий и динамики структуры (линейный, квадратический и нормированный коэффициенты, коэффициент Гатева). Для оценки существенности структурных различий в относительном выражении в международной аналитической практике широко применяются интегральные индексы А. Салаи и К. Гатева, учитывающие численность совокупности и количество выделенных групп в общем объеме изучаемого признака. С помощью данных показателей дается оценка динамики изменения структуры. Интегральный коэффициент структурных сдвигов К. Гатева учитывает интенсивность изменений по отдельным группам и удельный вес групп в сравниваемых структурах. Правило разложения дисперсии и его применение. Понятие о не сплошном наблюдении и ошибке репрезентативности. Виды не сплошного наблюдения. Принципы формирования выборочной совокупности. По охвату единиц совокупности статистическое наблюдение может быть проведено как сплошное и не сплошное. Сплошное наблюдение предусматривает обследование всех единиц изучаемой совокупности и связано с большими трудовыми и материальными затратами. Изучение не всех единиц совокупности, а лишь некоторой части, по которой следует судить о свойствах всей совокупности в целом, можно осуществить не сплошным наблюдением. В статистической практике самым распространенным является выборочное наблюдение. Только выборка позволяет распространить данные, полученные по части совокупности, на всю совокупность. Выборочное наблюдение – это такое не сплошное наблюдение, при котором отбор подлежащих обследованию единиц осуществляется в случайном порядке, отобранная часть изучается, а результаты распространяются на всю исходную совокупность. Наблюдение организуется таким образом, что эта часть отобранных единиц в уменьшенном масштабе репрезентирует(представляет) всю совокупность. Совокупность, из которой производится отбор, называется генеральной, и все ее обобщающие показатели – генеральными. Совокупность отобранных единиц именуют выборочной совокупностью, и все ее обобщающие показатели – выборочными. Имеется ряд причин, в силу которых, во многих случаях выборочному наблюдению отдается предпочтение перед сплошным. Наиболее существенны из них следующие: 1) экономия времени и средств в результате сокращения объема работы; 2) достижение большой точности результатов обследования благодаря сокращению ошибок, происходящих при регистрации; 3) сведение к минимуму порчи или уничтожения исследуемых объектов (это относится к изучению качества продукции – определение прочности пряжи при разрыве, испытание электрических лампочек на продолжительность горения, проверка консервов на доброкачественность); 4) необходимость детального исследования каждой единицы наблюдения при невозможности охвата всех единиц (при изучении бюджета семей). Использование выборочного метода является единственно возможным решением. Место выборочного наблюдения в современной практике отечественной и международнойстатистики Индексы как средние из индивидуальных. Особенности построения и анализа индексов цен Пааше, Ласпейреса и И.Фишера. В экономике в условиях рыночных отношений особое место среди индексов качественных показателей отводится индексу потребительских цен. С его помощью осуществляется оценка динамики цен и пересчет важнейших стоимостных показателей системы национальных счетов. Рассмотрим принцип построения агрегатных индексов качественных показателей на примере индекса цен. Если нам необходимо выявить изменения цен на различные продукты и товары или количества товаров и продуктов, то необходимо привести определенное количество товаров и продуктов по определенным ценам к общей стоимости. Для этого мы должны соизмерить "вес" каждого элемента (будь то цена или кол-во товара). При отражении изменения цен на товары в качестве весов будет выступать количество товара. Если же необходимо отразить изменение количества товаров, то в роли "весов" будут выступать цены. Но возникает проблема: на уровне какого периода зафиксировать веса (базисного или отчетного). Существует два способа расчета индексов цен: индексы цен Пааше и Лайспейреса. Индекс цен Ласпейреса Данный способ предлагает использование весов базисного периода
Экономическое содержание Индекс цен Ласпейреса показывает, на сколько изменились цены в отчетном периоде по сравнению с базисным, но на товары реализованные в базисном периоде. Иначе говоря индекс цен Ласпейреса показывает во сколько товары базисного периода подорожали или подешевели из-за изменения цен в отчетном периоде. Индекс цен Пааше Индекс цен Пааше — это агрегатный индекс цен с весами (количество реализованного товара) в отчетном периоде.
Идеальный индекс цен Фишера Представляет собой среднюю геометрическую из произведений двух агрегатных индексов цен Ласпейреса и Пааше:
Идеальность заключается в том, что индекс является обратимым во времени, то есть при перестановке базисного и отчетного периодов получается обратный индекс (величина обратная величине первоначального индекса). Индекс цен Фишера лишен какого-либо экономического содержания. В силу сложности расчета и трудности экономической интерпретации используется довольно редко (например, при исчислении индексов цен за длительный период времени для сглаживания значительных изменений)
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 428; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 . Впервые был введен в 1864 году экономистом Э.Ласпейресом.
. Впервые был введен в 1864 году экономистом Э.Ласпейресом.
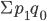 — стоимость продукции реализованной в базисном (предыдущем) периоде по ценам отчетного периода
— стоимость продукции реализованной в базисном (предыдущем) периоде по ценам отчетного периода — фактическая стоимость продукции в базисном периоде
— фактическая стоимость продукции в базисном периоде
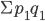 — фактическая стоимость продукции отчетного периода
— фактическая стоимость продукции отчетного периода — стоимость товаров реализованных в отчетном периоде по ценам базисного периода
— стоимость товаров реализованных в отчетном периоде по ценам базисного периода



