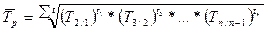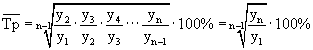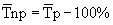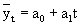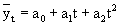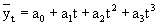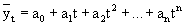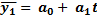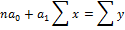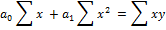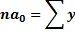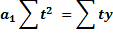Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 9. Вопрос 4. Средние аналитические показатели ряда динамики.Содержание книги
Поиск на нашем сайте
1. Средний уровень ряда динамики рассчитывается по средней хронологической, исчисленной из значений, изменяющихся во времени. В интервальных рядах с равноотстоящими интервалами применяется простая средняя арифметическая:
Для интервальных рядов с неравноотстоящими интервалами применяется взвешенная средняя арифметическая:
Для моментных рядов с равноотстоящими интервалами применяется простая средняя хронологическая величина:
Для моментных рядов с неравноотстоящими интервалами применяется взвешенная средняя хронологическая величина:
2. Средний абсолютный прирост определяется как простая средняя арифметическая величина из цепных абсолютных приростов и показывает, на сколько в среднем изменялся показатель в течение изучаемого периода времени:
3. Среднегодовой темп роста определяется как средняя геометрическая из цепных темпов роста и показывает, сколько процентов в среднем составлял рост показателя. Если цепные темпы роста опеределялись для рядов с равноотстоящими интервалами, то применяется простая средняя геометрическая величина:
где n – количество периодов времени. Если цепные темпы роста были определены для рядов с неравноотостоящими интервалами, то при расчете среднегодового темпа роста применяется взвешенная средняя геометрическая величина.
Необходимо помнить, что темпы роста должны быть выражены в виде коэффициентов.
4. Среднегодовой темп прироста определяется также, как и темп прироста и показывает, на сколько процентов в среднем рос показатель
Тема 9. Вопрос 5. Определение основной тенденции динамики на основе укрепления интервалов и скользящей средней. Метод укрепления интервалов. Если рассматривать уровни экономических показателей за короткие промежутки времени, то в силу влияния различных факторов, действующих в разных направлениях, в рядах динамики наблюдается снижение и повышение этих уровней. Это мешает видеть основную тенденцию развития изучаемого явления. В этом случае для наглядного представления тренда применяется метод укрупнения интервалов, который основан на укрупнении периодов времени, к которым относятся уровни ряда. Например, ряд ежесуточного выпуска продукции заменяется рядом месячного выпуска продукции и т. д. Метод простой скользящей средней. Сглаживание ряда динамики с помощью скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем средний уровень из такого же числа уровней, начиная со второго, далее – начиная с третьего и т. д. Таким образои, при расчетах среднего уровня как бы «скользят» по ряду динамики от его начала к концу, каждый раз отбрасывая один и уровень вначале и добавляя один следующий. Отсюда название – скользящая средняя. Тема 9. Вопрос 6. Определение основной тенденции динамики методом аналитического выравнивания. Аналитическое выравнивание предполагает представление уровней данного ряда динамики в виде функции времени - y=f(t). Для отображения основной тенденции развития явлений во времени применяются различные функции: полиномы степени, экспоненты, логистические кривые и другие виды. Полиномы имеют следующий вид: Полиномы имеют следующий вид: полином первой степени полином второй степени полином третьей степени полином n-ой степени
Здесь ао; а1; а2;... ап - параметры полиномов, t - условное обозначение времени. В статистической практике параметры полиномов невысокой степени иногда имеют конкретную интерпретацию характеристик динамического ряда. Так, параметр ао трактуется как характеристика средних условий ряда динамики, параметры аь а2, а3 - как изменения ускорени
для дальнейшего прогнозирования, используя модель линейной функции, необходимо решить систему уравнения, однако, если стоит задача – выровнять ряд динамики для выявления наличия тенденции, можно определить упрощенным методом вводится условное обозначение T, таким образом, чтобы сумма Т была равно 0
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 233; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.126.51 (0.005 с.) |

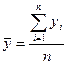
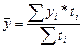
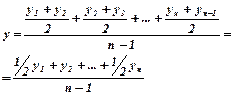
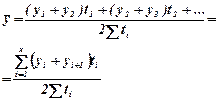
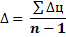
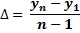
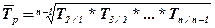 ,
,