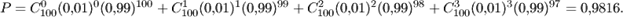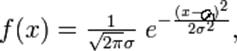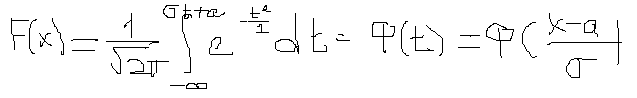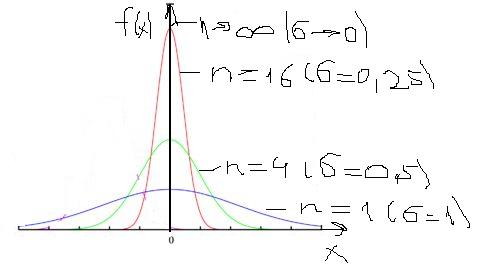Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Биномиальный закон (распределение Бернулли)Содержание книги
Поиск на нашем сайте
В общей форме биномиальный закон описывает осуществление признака в
где Производящая функция биномиального распределения задаётся формулой
Основные характеристики биномиального распределения (математическое ожидание и дисперсия):
Пример 1. Вероятность получения бракованного изделия равна 0,01. Какова вероятность того, что среди 100 изделий окажется не более 3 бракованных?
Решение. Пусть
Билет 7. Непрерывные и дискретные случайные величины. Плотность вероятности. Нормальный закон распределения. Математическое распределение и дисперсия. Графическое представление. Примеры.
Случайная величина (далее СВ) – величина, которая принимает значение в зависимости от стечения случайных обстоятельств. (Пр.: число больных на приеме врача, число студентов в аудитории, номер бочонка, когда его вынимают из мешка, при игре в лото и т.п.) СВ называется дискретной (далее – ДСВ), если она принимает счетное множество значений. (Пр.: число букв на произвольной странице книге, число волос на голове человека, число молекул в выделенном объеме газа и т.п.) СВ называется непрерывной (далее – НСВ), если она принимает любые значения внутри некоторого интервала. (Пр.: температура тела, масса зерен в колосьях пшеницы и т.п.) Вероятность - предел, к которому стремится частота события при неограниченном увеличении числа испытаний. (статистическое определение) P(A)=limn→∞(m/n) - отношение благоприятствующих случаев к общему числу равновозможных случаев к общему числу равновозможных несовместимых событий. (классическое опредедение) P(A)=(m/n) Распределение вероятностей — закон, описывающий область значений СВ и вероятности их принятия.
dP=f(x)dx dP – вероятность того, что НСВ Х принимает значения между х и х+dх. Вероятность dP прямо пропорциональна интервалу dx. f(x) – плотность вероятности (функция распределения вероятностей). Показывает, как изменяется вероятность, отнесенная к интервалу dx случайной величины, в зависимости от самой этой величины. f(x)=dP/dx x F(x)=∫f(x)dx - функция распределения НСВ. Равна вероятности того, что СВ -∞ принимает значения, меньшие х. F(x)=(-∞<X<x)
Нормальный закон распределения (закон Гаусса). СВ распределена по этому закону, если плотность вероятности имеет вид
a=M(X) – мат.ожидание СВ, σ – среднее квадратическое отклонение, σ2- дисперсия СВ. Дисперсия СВ – МО отклонения случайной величины от ее МО. D(X)=M[X-M(X)] Удобная формула: D(X)=M(X2)-[M(X)]2 Кривая закона носит колокообразную форму, симметричную относительно прямой х=а (центр рассеивания). В точке х=а функция достигает максимума.
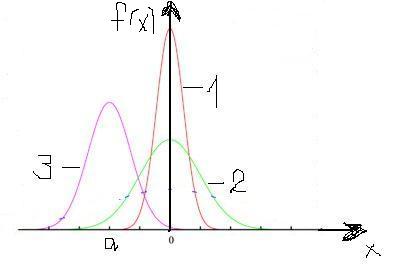
По мере возрастания |х-а| функция f(x) монотонно убывает, асимптотически приближаясь к нулю. С уменьшением σ кривая становится все более и более островершинной. Изменение а при постоянной σ не влияет на форму кривой, а лишь сдвигает ее вдоль оси абсцисс. Площадь, заключенной под кривой, согласно условию нормировки, равна единице. На рисунке изображены три кривые. Для кривых 1 и 2 а=0, но отличаются значением σ (σ1<σ2), кривая 3 имеет а≠0, σ=σ2. Вычислим функцию распределения.
Обычно используют иное выражение. Введем новую переменную t=(x-a)/σ. Следовательно, dx=σdt. Подставляем это в формулу.
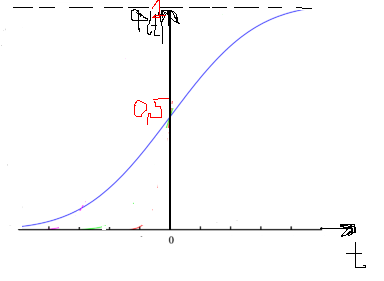
Значение функции Ф(t) обычно находят в составных таблицах, так как интеграл через элементарные функции не выражается. График:
Случайная величина при нормальном распределении может находится в интервале (х1, х2). Вероятность этого равна Р(х1<x<х2)=Ф((х2-а)/σ)-Ф((х1-а)/σ)
Допустим, что произвольно из нормальных распределений выбираются группы по n значений СВ. Для каждой группы можно найти средние значения (х1, х2, хi). Они сами образуют нормальное распределение (только среднему значению будет соответствовать не вероятность, а относительная частота). МО будет соответствовать исходному, дисперсия и среднее квадратическое отклонение – отличаться в n и в √n соответственно. Dn=D/n и σn=σ/√n. На рисунке представлены графики нормальных распределений, полученных для групп со значением n, равными 1, 4, 16 и n→∞. При n=1 – исходное распределение, σn=σ. При n→∞ σn→0, фактически «группа СВ» - все исходное распределение, среднее значение выражается одним числом и соответствует МО, к которому сводится все распределение.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 249; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.255.247 (0.006 с.) |

 испытаниях с возвратом. Наглядной схемой таких испытаний является последовательный выбор с возвращением шаров из урны, содержащей
испытаниях с возвратом. Наглядной схемой таких испытаний является последовательный выбор с возвращением шаров из урны, содержащей 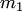 белых и
белых и 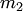 чёрных шаров. Если
чёрных шаров. Если  — число появления белых шаров в выборке из
— число появления белых шаров в выборке из 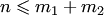 шаров, то
шаров, то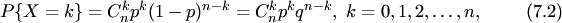
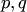 — вероятность появления при одном извлечении соответственно белого и чёрного,
— вероятность появления при одном извлечении соответственно белого и чёрного, 


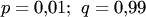 . Согласно биномиальному закону и закону сложения имеем
. Согласно биномиальному закону и закону сложения имеем