
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделювання економічних, екологічних та соціальних процесівСодержание книги
Поиск на нашем сайте 1. Статична модель «витрати-випуск» (модель міжгалузевого балансу) базується на понятті “чиста галузь” (галузі), тобто 2. Що таке 3. Модель Леонтьєва має вигляд: 4. Модель міжгалузевої залежності цін (врівноважених цін) має вигляд: 5. Критерій продуктивності моделі “витрати-випуск”: 6. Динамічна модель Леонтьєва має вигляд: 7. У моделі Леслі матриця Леслі, у якій 8. Якщо початковий розподіл чисельності популяції рівний 9. Доля особин популяції у моделі Леслі, яку можна взяти з популяції, щоб величина популяції була рівною вихідній, обчислюється (у відсотках) за формулою 10. Найбільше власне значення матриці Леслі і власний вектор, що відповідає цьому власному числу, означають відповідно: 11. Вікові структури мають 12. В основу моделі “хижак-жертва” покладені деякі умови про характер внутрішньо- та міжвидових стосунків у спільноті, одна з яких 13. В основу моделі “хижак-жертва” покладені деякі умови про характер внутрішньо- та міжвидових стосунків у спільноті, одна з яких 14. Якщо 15. Модель Леонтьєва – Форда має вигляд 16. У моделі Леонтьєва – Форда матриця 17. У моделі Леонтьєва – Форда матриця 18. У моделі Леонтьєва – Форда матриця 19. У моделі Леонтьєва - Форда матриця 20. У моделі Леонтьєва – Форда основне виробництво (виробництво випуску продукції) є рентабельним, якщо продуктивною є матриця 21. У моделі Леонтьєва – Форда допоміжне виробництво (виробництво знищення забруднювачів) є рентабельним, якщо продуктивною є матриця 22. Двоїста модель Леонтьєва-Форда відносно цін (модель міжгалузевих залежностей цін) має вигляд: 23. Неокласична задача споживання пов’язана з раціональним вибором набору благ та послуг споживачем при заданих функції корисності та визначеному бюджетному обмеженні має вигляд: 24. Короткостроковий період - це період у виробничій діяльності фірми, протягом якого вона може 25. Аксіома А2 монотонності теорії виробництва стверджує, що існує підмножина E простору витрат Х, яка називається економічною областю, в якій 26. Виробництво характеризується зростаючим доходом від розширення масштабу, 27. Неокласична модель поведінки однопродуктової фірми за певний (відносно невеликий) період часу (короткостроковий період) полягає 28. Гранична корисність – це 29. Виробнича функція Кобба-Дугласа має вигляд 30. Мультиплікативна функція корисності має вигляд: Теорія керування 1. Згідно з принципом оптимальності Беллмана 2. Для задачі оптимальної швидкодії функція Беллмана 3. Рівняння Беллмана задачі оптимальної швидкодії має вигляд 4. Рівняння Беллмана для задачі оптимального керування Больца має вигляд 5. Рівняння Беллмана для задачі оптимального керування Лагранжа має вигляд 6. Рівняння Беллмана для задачі оптимального керування Майєра має вигляд 7. Критерій оптимальності задачі Лагранжа має вигляд 8. Критерій оптимальності задачі Майєра має вигляд 9. Критерій оптимальності задачі Больца має вигляд 10. Задачу оптимального керування у формі Понтрягіна називають задачу вигляду 11. Диференціальним зв’язком називають рівняння вигляду 12. Лагранжіан для функції Лагранжа задачі оптимального керування у формі Понтрягіна має вигляд 13. Термінант для функції Лагранжа задачі оптимального керування у формі Понтрягіна має вигляд 14. Умови стаціонарності по 15. Умови трансверсальності по 16. Умови стаціонарності по 17. Умови доповнюючої нежорсткості теореми про принцип максимуму Понтрягіна мають вигляд: 18. Стаціонарна система, яку досліджують на керованість, має вигляд 19. Нестаціонарна система, яку досліджують на спостережуваність, має вигляд 20. Неперервні системи керування, об’єкти яких описуються звичайними диференціальними рівняннями, називають 21. Системи програмного керування – це такі системи, в яких 22. Система 23. Для цілком керованості стаціонарної системи 24. Для того, щоб існував розв’язок задачі спостережуваності системи 25. Розв’язок задачі спостережуваності системи 26. Нехай для кожного 27. Якщо для деякого 28. У теорії керування вектор 29. У теорії керування вважають, що параметри керування є 30. Якщо в системі 31. Якщо виконується умова цілком керованості системи
|
||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 255; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.103.111 (0.008 с.) |

 у статичній моделі «витрати-випуск» (моделі міжгалузевого балансу)
у статичній моделі «витрати-випуск» (моделі міжгалузевого балансу) матриці А задовольняло нерівність
матриці А задовольняло нерівність -це функція народжуваності,
-це функція народжуваності,  - функція, що характеризує перехід із однієї вікової структури в іншу, має вигляд:
- функція, що характеризує перехід із однієї вікової структури в іншу, має вигляд: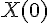 ,
,  основне рівняння моделі Леслі має вигляд
основне рівняння моделі Леслі має вигляд - густина популяції жертви;
- густина популяції жертви;  - густина популяції хижака;
- густина популяції хижака;  - швидкість розмноження популяції жертви за відсутності хижака;
- швидкість розмноження популяції жертви за відсутності хижака;  - природна смертність хижака;
- природна смертність хижака;  - питома швидкість споживання популяцією хижака популяції жертви при одиничній густині обох популяцій;
- питома швидкість споживання популяцією хижака популяції жертви при одиничній густині обох популяцій;  - коефіцієнт перетворення біомаси жертви, що була спожита хижаком, на його біомасу, тоді модель “хижак-жертва” має вигляд:
- коефіцієнт перетворення біомаси жертви, що була спожита хижаком, на його біомасу, тоді модель “хижак-жертва” має вигляд: - це
- це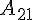 - це
- це - це
- це - це
- це – характеризує
– характеризує (рівняння Ейлера лагранжіана
(рівняння Ейлера лагранжіана  ) теореми про принцип максимуму Понтрягіна мають вигляд:
) теореми про принцип максимуму Понтрягіна мають вигляд: , коли границі
, коли границі 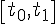 рухомі теореми про принцип максимуму Понтрягіна мають вигляд:
рухомі теореми про принцип максимуму Понтрягіна мають вигляд: називається цілком керованою, якщо
називається цілком керованою, якщо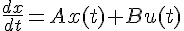 n-го порядку необхідно і достатньо, щоб
n-го порядку необхідно і достатньо, щоб з виходом
з виходом  необхідно і достатньо, щоб
необхідно і достатньо, щоб зводиться до знаходження керування
зводиться до знаходження керування  спряженої системи вигляду
спряженої системи вигляду існують і відомі n-1 похідні від вектора
існують і відомі n-1 похідні від вектора  системи
системи  . Тоді для існування розв’язку задачі спостережуваності даної системи в фіксованій точці
. Тоді для існування розв’язку задачі спостережуваності даної системи в фіксованій точці  достатньо, щоб
достатньо, щоб виконується умова
виконується умова  , де
, де  , тоді система
, тоді система  називають
називають стовпчик, то необхідна і достатня умова цілком керованості має вигляд
стовпчик, то необхідна і достатня умова цілком керованості має вигляд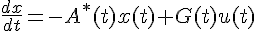 ,
,  , тоді виконується умова спостережуваності системи
, тоді виконується умова спостережуваності системи


