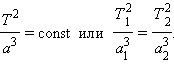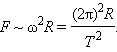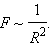Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы гидро- и аэродинамики
Движение жидкостей или газов представляет собой сложное явление. Для его описания используются различные упрощающие предположения (модели). В простейшей модели жидкость (или газ) предполагаются несжимаемыми и идеальными (т. е. без внутреннего трения между движущимися слоями). При движении идеальной жидкости не происходит превращения механической энергии во внутреннюю, поэтому выполняется закон сохранения механической энергии. Следствием этого закона для стационарного потока идеальной и несжимаемой жидкости является уравнение Бернулли (1738 г.). Стационарным принято называть такой поток жидкости, в котором не образуются вихри. В стационарном потоке частицы жидкости перемещаются по неизменным во времени траекториям, которые называются линиями тока. Опыт показывает, что стационарные потоки возникают только при достаточно малых скоростях движения жидкости. Рассмотрим стационарное движение идеальной несжимаемой жидкости по трубе переменного сечения (рис. 1.22.1). Различные части трубы могут находиться на разных высотах.
За промежуток времени Δ t жидкость в трубе сечением S 1 переместится на l 1 = υ1Δ t, а в трубе сечением S 2 – на l 2 = υ2Δ t, где υ1 и υ2 – скорости частиц жидкости в трубах. Условие несжимаемости записывается в виде:
Здесь Δ V – объем жидкости, протекшей через сечения S 1 и S 2. Таким образом, при переходе жидкости с участка трубы с большим сечением на участок с меньшим сечением скорость течения возрастает, т. е. жидкость движется с ускорением. Следовательно, на жидкость действует сила. В горизонтальной трубе эта сила может возникнуть только из-за разности давлений в широком и узком участках трубы. Давление в широком участке трубы должно быть больше чем в узком участке. Если участки трубы расположены на разной высоте, то ускорение жидкости вызывается совместным действием силы тяжести и силы давления. Сила давления - это упругая сила сжатия жидкости. Несжимаемость жидкости означает лишь то, что появление упругих сил происходит при пренебрежимо малом изменении объема любой части жидкости.
Так как жидкость предполагается идеальной, она течет по трубе без трения. Поэтому к ее течению можно применить закон сохранения механической энергии. При перемещении жидкости силы давления совершают работу:
Работа Δ A сил давления равна изменению потенциальной энергии упругой деформации жидкости, взятому с обратным знаком. Изменения, произошедшие за время Δ t в выделенной части жидкости, заключенной между сечениями S 1 и S 2 в начальный момент времени, при стационарном течении сводятся к перемещению массы жидкости Δ m = ρΔ V (ρ – плотность жидкости) из одной части трубы сечением S 1 в другую часть сечением S 2 (заштрихованные объемы на рис. 1.22.1). Закон сохранения механической энергии для этой массы имеет вид:
где E 1 и E 2 – полные механические энергии массы Δ m в поле тяготения:
Отсюда следует:
Это и есть уравнение Бернулли. Из него следует, что сумма
остается неизменной вдоль всей трубы. В частности, для горизонтально расположенной трубы (h 1 = h 2) уравнение Бернулли принимает вид:
Величина p – статическое давление в жидкости. Оно может быть измерено с помощью манометра, перемещающегося вместе с жидкостью. Практически давление в разных сечениях трубы измеряется с помощью манометрических трубок, вставленных через боковые стенки в поток жидкости, так чтобы нижние концы трубок были параллельны скоростям частиц жидкости (рис. 1.22.2). Из уравнения Бернулли следует: Давление в жидкости, текущей по горизонтальной трубе переменного сечения, больше в тех сечениях потока, в которых скорость ее движения меньше, и наоборот, давление меньше в тех сечениях, в которых скорость больше.
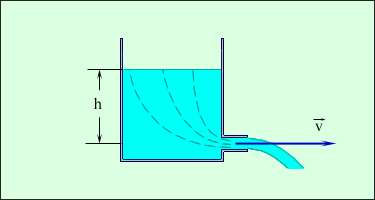
Если сечение потока жидкости достаточно велико, то уравнение Бернулли следует применять к линиям тока, т. е. линиям, вдоль которых перемещаются частицы жидкости при стационарном течении. Например, при истечении идеальной несжимаемой жидкости из отверстия в боковой стенке или дне широкого сосуда линии тока начинаются вблизи свободной поверхности жидкости и проходят через отверстие (рис. 1.22.3).
Поскольку скорость жидкости вблизи поверхности в широком сосуде пренебрежимо мала, то уравнение Бернулли принимает вид:
где p 0 – атмосферное давление, h – перепад высоты вдоль линии тока. Таким образом,
Это выражение для скорости истечения называют формулой Торричелли. Скорость истечения идеальной жидкости из отверстия в сосуде такая же, как и при свободном падении тела с высоты h без начальной скорости. В отличие от жидкостей, газы могут сильно изменять свой объем. Расчеты показывают, что сжимаемостью газов можно пренебречь, если наибольшие скорости в потоке малы по сравнению со скоростью звука в этом газе. Таким образом, уравнение Бернулли можно применять к достаточно широкому классу задач аэродинамики. Одной из таких задач является изучение сил, действующих на крыло самолета. Строгое теоретическое решение этой задачи чрезвычайно сложно, и обычно для исследования сил применяются экспериментальные методы. Уравнение Бернулли позволяет дать лишь качественное объяснение возникновению подъемной силы крыла. На рис. 1.22.4 изображены линии тока воздуха при обтекании крыла самолета. Из-за специального профиля крыла и наличия угла атаки, т. е. угла наклона крыла по отношению к набегающему потоку воздуха, скорость воздушного потока над крылом оказывается больше, чем под крылом. Поэтому на рис. 1.22.4 линии тока над крылом располагаются ближе друг к другу, чем под крылом. Из уравнения Бернулли следует, что давление в нижней части крыла будет больше, чем в верхней; в результате появляется сила
Теория подъемной силы крыла самолета была создана Н. Е. Жуковским. Он показал, что существенную роль при обтекании крыла играют силы вязкого трения в поверхностном слое. В результате их действия возникает круговое движение (циркуляция) воздуха вокруг крыла (зеленые стрелки на рис. 1.22.4). В верхней части крыла скорость циркулирующего воздуха складывается со скоростью набегающего потока, в нижней части эти скорости направлены в противоположные стороны. Это и приводит к возникновению разности давлений и появлению подъемной силы. Циркуляция воздуха, обусловленная силами вязкого трения, возникает и вокруг вращающегося тела (например, цилиндра). При вращении цилиндр увлекает прилегающие слои воздуха, вызывая его циркуляцию. Если такой цилиндр установить в набегающем потоке воздуха, то возникнет сила бокового давления, аналогичная подъемной силе крыла самолета. Это явление называется эффектом Магнуса. Рис. 1.22.5 иллюстрирует обтекание вращающегося цилиндра набегающим потоком. Эффект Магнуса проявляется, например, при полете закрученного мяча при игре в теннис или футбол.
Итак, во многих явлениях аэродинамики существенную роль играют силы вязкого трения. Они приводят к возникновению циркулирующих потоков воздуха вокруг крыла самолета или вокруг вращающегося тела, к появлению силы сопротивления среды и т. д. Уравнение Бернулли не учитывает сил трения. Его вывод основан на законе сохранения механической энергии при течении жидкости или газа. Поэтому с помощью уравнения Бернулли нельзя дать исчерпывающего объяснения явлений, в которых проявляются силы трения. В этих случаях можно руководствоваться только качественными соображениями – чем больше скорость, тем меньше давление в потоке газа. Особенно заметно проявляются силы вязкого трения при течении жидкостей. У некоторых жидкостей вязкость настолько велика, что применение уравнение Бернулли может привести к качественно неверным результатам. Например, при истечении вязкой жидкости через отверстие в стенке сосуда ее скорость может быть в десятки раз меньше рассчитанной по формуле Торричелли. При движении сферического тела в идеальной жидкости оно не должно испытывать лобового сопротивления. Если же такое тело движется в вязкой жидкости, то возникает сила сопротивления, модуль которой пропорционален скорости υ и радиусу сферы r (закон Стокса)
Коэффициент пропорциональности в этой формуле зависит от свойств жидкости. Поэтому, если тяжелый шарик бросить в высокий сосуд, наполненный вязкой жидкостью (например, глицерином), то через некоторое время скорость шарика достигнет установившегося значения, которое не будет изменяться при дальнейшем движении шарика. При движении с установившейся скоростью силы, действующие на шарик (сила тяжести Глава 1. Механика Вращение твердого тела Для кинематического описания вращения твердого тела удобно использовать угловые величины: угловое перемещение Δφ, угловую скорость ω
и угловое ускорение ε
В этих формулах углы выражаются в радианах. При вращении твердого тела относительно неподвижной оси все его точки движутся с одинаковыми угловыми скоростями и одинаковыми угловыми ускорениями. За положительное направление вращения обычно принимают направление против часовой стрелки.
При малых угловых перемещениях Δφ модуль вектора
где r – модуль радиус-вектора
и между модулями линейного и углового ускорения:
Векторы
Разобьем вращающееся тело на малые элементы Δ m i. Расстояния до оси вращения обозначим через r i, модули линейных скоростей – через υi. Тогда кинетическую энергию вращающегося тела можно записать в виде:
Физическая величина
В пределе при Δ m → 0 эта сумма переходит в интеграл. Единица измерения момента инерции в СИ – килограмм-метр в квадрате (кг∙м2). Таким образом, кинетическую энергию твердого тела, вращающегося относительно неподвижной оси, можно представить в виде
Эта формула очень похожа на выражение для кинетической энергии поступательно движущегося тела Момент инерции в динамике вращательного движения играет ту же роль, что и масса тела в динамике поступательного движения. Но есть и принципиальная разница. Если масса – внутреннее свойство данного тела, не зависящее от его движения, то момент инерции тела зависит от того, вокруг какой оси оно вращается. Для разных осей вращения моменты инерции одного и того же тела различны. Во многих задачах рассматривается случай, когда ось вращения твердого тела проходит через его центр массы. Положение x C, y C центра масс для простого случая системы из двух частиц с массами m 1 и m 2, расположенными в плоскости XY в точках с координатами x 1, y 1 и x 2, y 2 (рис. 1.23.2), определяется выражениями:
В векторной форме это соотношение принимает вид:
Аналогично, для системы из многих частиц радиус-вектор
Для сплошного тела суммы в выражении для
Равнодействующая сил тяжести в однородном поле тяготения приложена к центру масс тела. Если тело подвешено за центр масс, то оно находится в безразличном состоянии равновесия (см. §1.14). Любое движение твердого тела можно представить как сумму двух движений: поступательного движения со скоростью центра масс тела и вращения относительно оси, проходящей через центр масс. Примером может служить колесо, которое катится без проскальзывания по горизонтальной поверхности (рис. 1.23.4). При качении колеса все его точки движутся в плоскостях, параллельных плоскости рисунка. Такое движение называется плоским. При плоском движении кинетическая энергия движущегося твердого тела равна сумме кинетической энергии поступательного движения и кинетической энергии вращения относительно оси, проходящей через центр масс тела и перпендикулярной плоскостям, в которых движутся все точки тела:
где m – полная масса тела, I C – момент инерции тела относительно оси, проходящей через центр масс.
В механике доказывается теорема о движении центра масс: под действием внешних сил центр масс любого тела или системы взаимодействующих тел движется как материальная точка, в которой сосредоточена вся масса системы. Иллюстрацией этого утверждения может служить рис. 1.23.5, на котором изображено движение тела под действием силы тяжести. Центр масс тела движется по параболической траектории как материальная точка, в то время как все другие точки движутся по более сложным траекториям.
Если твердое тело вращается относительно некоторой неподвижной оси, то его момент инерции I можно выразить через момент инерции I C этого тела относительно оси, проходящей через центр масс тела и параллельной первой.
Рассмотрим сечение твердого тела произвольной формы, изображенное на рис. 1.23.6. Выберем координатную систему XY с началом координат O в центре масс C тела. Пусть одна из осей вращения проходит через центр масс C, а другая через произвольную точку P, расположенную на расстоянии d от начала координат. Обе оси перпендикулярны плоскости чертежа. Пусть Δ m i – некоторый малый элемент массы твердого тела. По определению момента инерции:
Выражение для I P можно переписать в виде:
Поскольку начало координат совпадает с центром масс C, последние два члена обращаются в нуль. Это следует из определения центра масс. Следовательно,
где m – полная масса тела. Этот результат называют теоремой Штейнера (теоремой о параллельном переносе оси вращения). На рис. 1.23.7 изображены однородные твердые тела различной формы и указаны моменты инерции этих тел относительно оси, проходящей через центр масс.
Второй закон Ньютона может быть обобщен на случай вращения твердого тела относительно неподвижной оси. На рис. 1.23.8 изображено некоторое твердое тело, вращающееся относительно оси, перпендикулярной плоскости рисунка и проходящей через точку O. Выделим произвольный малый элемент массы Δ m i. На него действуют внешние и внутренние силы. Равнодействующая всех сил есть
Касательная составляющая
где Если обе части написанного выше уравнения умножить на r i, то мы получим:
Здесь l i – плечо силы Теперь нужно аналогичные соотношения записать для всех элементов массы Δ m i вращающегося твердого тела, а затем просуммировать левые и правые части. Это дает:
Стоящая в правой части сумма моментов сил, действующих на различные точки твердого тела, состоит из суммы моментов всех внешних сил и суммы моментов всех внутренних сил.
Но сумма моментов всех внутренних сил согласно третьему закону Ньютона равна нулю, поэтому в правой части остается только сумма моментов всех внешних сил, которые мы будем обозначать через M. В итоге:
Это и есть основное уравнение динамики вращательного движения твердого тела. Угловое ускорение ε и момент сил M в этом уравнении являются величинами алгебраическими. Обычно за положительное направление вращения принимают направление против часовой стрелки. Возможна и векторная форма записи основного уравнения динамики вращательного движения, при которой величины При изучении поступательного движения тел вводится понятие импульса тела Моментом импульса вращающегося тела называют физическую величину, равную произведению момента инерции тела I на угловую скорость ω его вращения. Момент импульса обозначается буквой L:
Поскольку
Окончательно будем иметь:
Это уравнение, полученное здесь для случая, когда I = const, справедливо и в общем случае, когда момент инерции тела изменяется в процессе движения. Если суммарный момент М внешних сил, действующих на тело, равен нулю, то момент импульса L = I ω относительно данной оси сохраняется:
Следовательно,
Это и есть закон сохранения момента импульса. Иллюстрацией этого закона может служить неупругое вращательное столкновение двух дисков, насажанных на общую ось (рис. 1.23.9).
Закон сохранения момента импульса справедлив для любой замкнутой системы тел. Он выполняется, например, при движении планет по эллиптическим орбитам вокруг Солнца (второй закон Кеплера – см. §1.24). Уравнение вращательного движения тела можно записывать не только относительно неподвижной или равномерно движущейся оси, но и относительно оси, движущейся с ускорением. Основное уравнение динамики вращательного движения не изменяет своего вида и в случае ускоренно движущихся осей при условии, что ось вращения проходит через центр массы тела и что ее направление в пространстве остается неизменным. Примером может служить качение тела (обруч, цилиндр, шар) по наклонной плоскости с трением (рис. 1.23.10).
Ось вращения O проходит через центр масс тела. Моменты силы тяжести Уравнение вращательного движения:
где ε – угловое ускорение катящегося тела, a – линейное ускорение его центра масс, I C – момент инерции относительно оси O, проходящей через центр масс. Второй закон Ньютона для поступательного движения центра масс записывается в виде:
Исключая из этих уравнений F тр, получим окончательно:
Из этого выражения видно, что быстрее будет скатываться с наклонной плоскости тело, обладающее меньшим моментом инерции. Например, у шара Законы Кеплера В мире атомов и элементарных частиц гравитационные силы пренебрежимо малы по сравнению с другими видами силового взаимодействия между частицами. Очень непросто наблюдать гравитационное взаимодействие и между различными окружающими нас телами, даже если их массы составляют многие тысячи килограмм. Однако именно гравитация определяет поведение «больших» объектов, таких, как планеты, кометы и звезды, именно гравитация удерживает всех нас на Земле. Гравитация управляет движением планет Солнечной системы. Без нее планеты, составляющие Солнечную систему, разбежались бы в разные стороны и потерялись в безбрежных просторах мирового пространства. Закономерности движения планет с давних пор привлекали внимание людей. Изучение движения планет и строения Солнечной системы и привело к созданию теории гравитации – открытию закона всемирного тяготения. С точки зрения земного наблюдателя планеты движутся по весьма сложным траекториям (рис. 1.24.1). Первая попытка создания модели Вселенной была предпринята Птолемеем (~ 140 г.). В центре мироздания Птолемей поместил Землю, вокруг которой по большим и малым кругам, как в хороводе, двигались планеты и звезды.
Геоцентрическая система Птолемея продержалась более 14 столетий и только в середине XVI века была заменена гелиоцентрической системой Коперника. В системе Коперника траектории планет оказались более простыми. Немецкий астроном И. Кеплер в начале XVII века на основе системы Коперника сформулировал три эмпирических закона движения планет Солнечной системы. Кеплер использовал результаты наблюдений за движением планет датского астронома Т. Браге. Первый закон Кеплера (1609 г.): Все планеты движутся по эллиптическим орбитам, в одном из фокусов которых находится Солнце. На рис. 1.24.2 показана эллиптическая орбита планеты, масса которой много меньше массы Солнца. Солнце находится в одном из фокусов эллипса. Ближайшая к Солнцу точка P траектории называется перигелием, точка A, наиболее удаленная от Солнца, называется афелием или апогеем. Расстояние между афелием и перигелием – большая ось эллипса.
Почти все планеты Солнечной системы (кроме Плутона) движутся по орбитам, близким к круговым. Второй закон Кеплера (1609 г.): Радиус-вектор планеты описывает в равные промежутки времени равные площади. Рис. 1.24.3 иллюстрирует 2-ой закон Кеплера.
Второй закон Кеплера эквивалентен закону сохранения момента импульса. На рис. 1.24.3 изображен вектор импульса тела
Здесь Момент импульса L по абсолютной величине равен произведению модулей векторов
Из этих отношений следует:
Поэтому, если по второму закону Кеплера В частности, поскольку скорости планеты в перигелии
Третий закон Кеплера (1619 г.): Квадраты периодов обращения планет относятся как кубы больших полуосей их орбит:
Третий закон Кеплера выполняется для всех планет Солнечной системы с точностью выше 1 %. На рис. 1.24.4 изображены две орбиты, одна из которых круговая с радиусом R, а другая – эллиптическая с большой полуосью a. Третий закон утверждает, что если R = a, то периоды обращения тел по этим орбитам одинаковы.
Несмотря на то, что законы Кеплера явились важнейшим этапом в понимании движения планет, они все же оставались только эмпирическими правилами, полученными из астрономических наблюдений. Законы Кеплера нуждались в теоретическом обосновании. Решающий шаг в этом направлении был сделан Исааком Ньютоном, открывшим в 1682 году закон всемирного тяготения:
где M и m – массы Солнца и планеты, r – расстояние между ними, G = 6,67·10–11 Н·м2/кг2 – гравитационная постоянная. Ньютон первый высказал мысль о том, что гравитационные силы определяют не только движение планет Солнечной системы; они действуют между любыми телами Вселенной. В частности, сила тяжести, действующая на тела вблизи поверхности Земли, имеет гравитационную природу. Для круговых орбит первый и второй закон Кеплера выполняются автоматически, а третий закон утверждает, что T 2 ~ R 3, где Т – период обращения, R – радиус орбиты. Отсюда можно получить зависимость гравитационной силы от расстояния. При движении планеты по круговой траектории на нее действует центростремительная сила, которая возникает за счет гравитационного взаимодействия планеты и Солнца:
Если T 2 ~ R 3, то
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 618; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.216.229 (0.092 с.) |








 действующая на крыло. Вертикальная составляющая
действующая на крыло. Вертикальная составляющая  этой силы называется подъемной силой. Подъемная сила позволяет скомпенсировать силу тяжести, действующую на самолет, и тем самым она обеспечивает возможность полета тяжелых летательных аппаратов в воздухе. Горизонтальная составляющая
этой силы называется подъемной силой. Подъемная сила позволяет скомпенсировать силу тяжести, действующую на самолет, и тем самым она обеспечивает возможность полета тяжелых летательных аппаратов в воздухе. Горизонтальная составляющая  представляет собой силу сопротивления среды.
представляет собой силу сопротивления среды.

 выталкивающая сила
выталкивающая сила 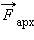 и сила сопротивления среды
и сила сопротивления среды  ), оказываются скомпенсированными, и их равнодействующая равна нулю.
), оказываются скомпенсированными, и их равнодействующая равна нулю.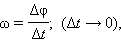


 линейного перемещения некоторого элемента массы Δ m вращающегося твердого тела выражается соотношением:
линейного перемещения некоторого элемента массы Δ m вращающегося твердого тела выражается соотношением: (рис. 1.23.1). Отсюда следует связь между модулями линейной и угловой скоростей:
(рис. 1.23.1). Отсюда следует связь между модулями линейной и угловой скоростей: и
и  направлены по касательной к окружности радиуса r. Следует вспомнить, что при движении тела по окружности возникает также нормальное или центростремительное ускорение, модуль которого есть
направлены по касательной к окружности радиуса r. Следует вспомнить, что при движении тела по окружности возникает также нормальное или центростремительное ускорение, модуль которого есть

 зависит от распределения масс вращающегося тела относительно оси вращения. Она называется моментом инерции I тела относительно данной оси:
зависит от распределения масс вращающегося тела относительно оси вращения. Она называется моментом инерции I тела относительно данной оси: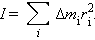

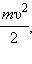 только теперь вместо массы m в формулу входит момент инерции I, а вместо линейной скорости υ – угловая скорость ω.
только теперь вместо массы m в формулу входит момент инерции I, а вместо линейной скорости υ – угловая скорость ω.


 центра масс определяется выражением
центра масс определяется выражением



 и вращения (2) с угловой скоростью
и вращения (2) с угловой скоростью  относительно оси O, проходящей через центр масс.
относительно оси O, проходящей через центр масс.






 Ее можно разложить на две составляющие: касательную составляющую
Ее можно разложить на две составляющие: касательную составляющую  и радиальную
и радиальную  Радиальная составляющая создает центростремительное ускорение a n.
Радиальная составляющая создает центростремительное ускорение a n.
 составляющие силы
составляющие силы  действующей на элемент Δ m i твердого тела.
действующей на элемент Δ m i твердого тела.
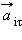 массы Δ m i. Второй закон Ньютона, записанный в скалярной форме, дает
массы Δ m i. Второй закон Ньютона, записанный в скалярной форме, дает – угловое ускорение всех точек твердого тела.
– угловое ускорение всех точек твердого тела.
 , M i – момент силы.
, M i – момент силы.

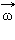 ,
,  ,
,  определяются как векторы, направленные по оси вращения.
определяются как векторы, направленные по оси вращения. (см. §1.16). Аналогично, при изучении вращательного движения вводится понятие момента импульса.
(см. §1.16). Аналогично, при изучении вращательного движения вводится понятие момента импульса. уравнение вращательного движения можно представить в виде:
уравнение вращательного движения можно представить в виде:



 и силы реакции
и силы реакции  относительно оси O равны нулю. Момент M создает только сила трения: M = F тр R.
относительно оси O равны нулю. Момент M создает только сила трения: M = F тр R.

 а у сплошного однородного цилиндра
а у сплошного однородного цилиндра  Следовательно, шар будет скатываться быстрее цилиндра.
Следовательно, шар будет скатываться быстрее цилиндра.


 и
и  Площадь, заметенная радиус-вектором за малое время Δ t, приближенно равна площади треугольника с основанием r Δθ и высотой r:
Площадь, заметенная радиус-вектором за малое время Δ t, приближенно равна площади треугольника с основанием r Δθ и высотой r:
 – угловая скорость (см. §1.6).
– угловая скорость (см. §1.6). и
и 


 то и момент импульса L при движении остается неизменным.
то и момент импульса L при движении остается неизменным. и афелии
и афелии  направлены перпендикулярно радиус-векторам
направлены перпендикулярно радиус-векторам  и
и  из закона сохранения момента импульса следует:
из закона сохранения момента импульса следует: