Виртуальные каналы в сетях с коммутацией пакетов

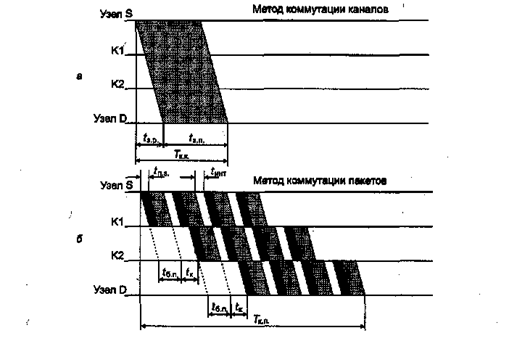
Описанный выше режим передачи пакетов между двумя конечными узлами сети предполагает независимую маршрутизацию каждого пикета. Такой режим работы сети называется дейтаграммным, и при его использовании коммутатор может из­менить маршрут какого-либо пакета в зависимости от состояния сети — работоспособности каналов и других коммутаторов, длины очередей пакетов в соседних коммутаторах и т. п.

Существует и другой режим работы сети — передача пакетов по виртуальному каналу (virtual circuit или virtual channel). В этом случае перед тем, как начать передачу данных между двумя конечными узлами, должен быть установлен вирту­альный канал, который представляет собой единственный маршрут, соединяющий эти конечные узлы. Виртуальный канал может быть динамическим или постоян­ным. Динамический виртуальный канал устанавливается при передаче в сеть спе­циального пакета — запроса на установление соединения. Этот пакет проходит через коммутаторы и «прокладывает» виртуальный канал. Это означает, что коммутато­ры запоминают маршрут для данного соединения и при поступлении последую­щих пакетов данного соединения отправляют их всегда по проложенному маршруту. Постоянные виртуальные каналы создаются администраторами сети путем ручной настройки коммутаторов.

При отказе коммутатора или канала на пути виртуального канала соединение разрывается, и виртуальный канал нужно прокладывать заново. При этом он, есте­ственно, обойдет отказавшие участки сети.

Каждый режим передачи пакетов имеет свои преимущества и недостатки. Дейтаграммный метод не требует предварительного установления соединения и поэтому работает без задержки перед передачей данных. Это особенно выгодно для переда­чи небольшого объема данных, когда время установления соединения может быть соизмеримым со временем передачи данных. Кроме того, дейтаграммный метод быстрее адаптируется к изменениям в сети.

При использовании метода виртуальных каналов время, затраченное на установление виртуального канала, компенсируется последующей быстрой передачей

всего потока пакетов. Коммутаторы распознают принадлежность пакета к вирту­альному каналу по специальной метке — номеру виртуального канала, а не анали­зируют адреса конечных узлов, как это делается при дейтаграммном методе.

Пропускная способность сетей с коммутацией пакетов

Одним из отличий метода коммутации пакетов от метода коммутации каналов является неопределенность пропускной способности соединения между двумя або­нентами. В методе коммутации каналов после образования составного канала про­пускная способность сети при передаче данных между конечными узлами известна — это пропускная способность канала. Данные после задержки, связанной с уста­новлением канала, начинают передаваться на максимальной для канала скорости (рис. 2.31, а). Время передачи сообщения в сети с коммутацией каналов Тк.к. равно сумме задержки распространения сигнала по линии связи t з.р. и задержки передачи сообщения t з.п. Задержка распространения сигнала зависит от скорости распростра­нения электромагнитных волн в конкретной физической среде, которая колеблет­ся от 0,6 до 0,9 скорости света в вакууме. Время передачи сообщения равно V/C, где V — объем сообщения в битах, а С — пропускная способность канала в битах в секунду.

В сети с коммутацией пакетов наблюдается принципиально другая картина.

Выводы

* Сети с коммутацией пакетов были специально разработаны для эффективной передачи пульсирующего компьютерного трафика. Буферизация пакетов разных абонентов в коммутаторах позволяет сгладить неравномерности интенсив­ности трафика каждого абонента и равномерно загрузить каналы связи между
коммутаторами.

* Сети с коммутацией пакетов эффективно работают в том отношении, что объем передаваемых данных от всех абонентов сети в единицу времени больше, чем при использовании сети с коммутацией каналов. Однако для каждой пары або­нентов пропускная способность сети может оказаться ниже, чему сети с ком­мутацией каналов, за счет очередей пакетов в коммутаторах.

* Сети с коммутацией пакетов могут работать в одном из двух режимов; дейтаграммном режиме или режиме виртуальных каналов.

Размер пакета существенно влияет на производительность сети. Обычно паке­ты в сетях имеют максимальный размер в 1-4 Кбайт.

 

Старший преподаватель кафедры №24 подполковник________ Баричев С. Г.

 

Военная академия Ракетных войск стратегического назначения

имени Петра Великого

 

Кафедра №24

 

ЛЕКЦИЯ №8 «ПРОБЛЕМА ЗАЩИТЫ ИНФОРМАЦИИ»

 

ПО УЧЕБНОЙ ДИСЦИПЛИНЕ: « ИНФОРМАЦИОННЫЕ СЕТИ И ТЕЛЕКОММУНИКАЦИИ»

 

Автор(ы ): Баричев С.Г., КТН, старший преподаватель;

 

Рассмотрено и одобрено на заседании кафедры (ПМК кафедры)

Протокол № ___ от «___» _______ 2008 г.

МОСКВА 2008

Лекция №8

Тема: Проблема защиты информации

Вопросы:

1) Угрозы безопасности информации

2) Принципы защиты информации

 

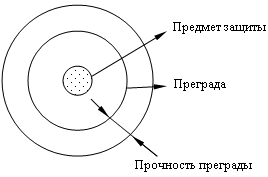
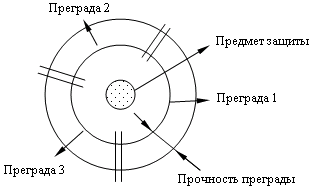
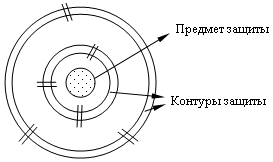
Угрозы безопасности информации и их классификация.
Угроза - это потенциально возможное событие, действие, процесс или явление, которое может привести к понятию ущерба чьим-либо интересам.
Нарушение безопасности - это реализация угрозы.
Естественные угрозы - это угрозы, вызванные воздействием на АС объективных физических процессов, стихийных природных явлений, не зависящих от человеека.
Естественные делятся на:

природные (стихийные бедствия, магнитные бури, радиоактивное излучение, осадки)

технические. Связаны надежностью технических средств, обработки информации и систем обеспечения.

Искусственные делят на:

непреднамеренные - совершенные по незнанию и без злого умысла, из любопытности или халатности

преднамеренные

Каналы проникновения в систему и их классификация:

По способу:

прямые

косвенные

По типу основного средства для реализации угрозы:

человек

аппаратура

программа

По способу получения информации:

физический

электромагнитный

информационный

Меры противодействия угрозам:

Правовые и законодательные.
Законы, указы, нормативные акты, регламентирующие правила обращения с информацией и определяющие ответственность за нарушение этих правил.

Морально-этические.
Нормы поведения, которые традиционно сложились или складываются в обществе по мере распространения вычислительной техники. Невыполнение этих норм ведет к падению авторитета, престижа организации, страны, людей.

Административные или организационные.
Меры организационного характера, регламентирующие процессы функционирования АС, деятельность персонала с целью максимального затруднения или исключения реализации угроз безопасности:

организация явного или скрытого контроля за работой пользователей

организация учета, хранения, использования, уничтожения документов и носителей информации.

организация охраны и надежного пропускного режима

мероприятия, осуществляемые при подборе и подготовке персонала

мероприятия по проектированию, разработке правил доступа к информации

мероприятия при разработке, модификации технических средств

Физические.
Применение разного рода технических средств охраны и сооружений, предназначенных для создания физических препятствий на путях проникновения в систему.

Технические.
Основаны на использовании технических устройств и программ, входящих в состав АС и выполняющих функции защиты:

средства аутентификации

аппаратное шифрование

другие

Принципы построения систем защиты:

Принцип системности - системный подход предполагает необходимость учета всех взаимосвязанных и изменяющихся во времени элементов, условий и факторов, существенно значимых для понимания и решения проблемы обеспечения безопасности.

Принцип компетентности - предполагает построение системы из разнородных средств, перекрывающих все существующие каналы реализации угрозы безопасности и не содержащих слабых мест на стыке отдельных компонентов.

Принцип непрерывной защиты - защита должна существовать без разрыва в пространстве и времени. Это непрерывный целенаправленный процесс, предполагающий не только защиту эксплуатации, но и проектирование защиты на стадии планирования системы.

Принцип разумной достаточности. Вложение средств в систему защиты должно быть построено таким образом, чтобы получить максимальную отдачу.

Принцип гибкости управления и применения. При проектировании системы защита может получиться либо избыточной, либо недостаточной. Система защиты должна быть легко настраиваема.

Принцип открытости алгоритмов и механизмов защиты. Знание алгоритма механизма защиты не позволяет осуществить взлом системы.

Принцип простоты применения защитных мер и средств. Все механизмы защиты должны быть интуитивно понятны и просты в использовании. Пользователь должен быть свободен от выполнения малопонятной многообъемной рутиной работы и не должен обладать специальными знаниями.

Модель элементарной защиты.

Прочность защитной преграды является достаточной, если ожидаемое время преодоления ее нарушителем больше времени жизни предмета защиты, или больше времени обнаружения и блокировки его доступа при отсутствии путей скрытого обхода этой преграды.

Модель многозвенной защиты.

Модель многоуровневой защиты.

 

Старший преподаватель кафедры №24 подполковник________ Баричев С. Г.

 

 

Военная академия Ракетных войск стратегического назначения

имени Петра Великого

 

Кафедра №24

 

ЛЕКЦИЯ №9 «КОД ХЭММИНГА»

 

ПО УЧЕБНОЙ ДИСЦИПЛИНЕ: « ИНФОРМАЦИОННЫЕ СЕТИ И ТЕЛЕКОММУНИКАЦИИ»

 

Автор(ы ): Баричев С.Г., КТН, старший преподаватель;

 

Рассмотрено и одобрено на заседании кафедры (ПМК кафедры)

Протокол № ___ от «___» _______ 2008 г.

Пусть нам предстоит закодировать текст, записанный на некотором языке, таком, что число букв в алфавите этого языка n = 2^m (m целое число), а появление в тексте тех или иных букв алфавита равновероятно и не зависит от того, какие буквы им предшествовали. Тогда имеем
p(i) = p(j) = 1/n; H = log₂ = m.
Условия задачи таковы, что достичь оптимального кодирования можно самым незатейливым методом кодирования - побуквенным кодированием с постоянной длиной (l = m) кодовых наборов. При этом, однако, мы оказались бы лишенными какой-либо возможности обнаруживать, а тем более исправлять ошибки. Чтобы такая возможность появилась, необходимо отказаться от оптимальности кода, "раскошелиться" на несколько дополнительных двоичных символов на букву, т.е. умышленно ввести некоторую избыточность, которая смогла бы помочь нам обнаружить или исправить ошибки. Необходимое число дополнительно вводимых двоичных символов на одну букву обозначим через x, и тогда длина кодового набора станет равной l = m + x. Примем, что в результате помех (случайных или преднамеренных) лишь один или вовсе никакой из m + x двоичных символов может превращаться из единицы в нуль или, наоборот, из нуля в единицу. Примем далее, что 1 + m + x событий, заключающиеся в том, что ошибка вообще не произойдет, произойдет на уровне первого, второго,.... (m + x)-го символа кодового набора, равновероятны. Энтропию угадывания того, какое именно из этих 1 + m + x событий будет иметь место, в силу равновероятности этих событий можно определить по формуле Н = log₂ (1 + m + х) бит. Таким образом, для обнаружения самого факта наличия одиночной ошибки и установления ее позиции необходимо заполучить информацию в количестве не менее Н = log₂(1 + m + x) бит. Источником этой информации служат лишь дополнительно введенные x двоичных символов, так как остальные m символов из-за оптимальности кодирования до предела заняты описанием самого текста. Заметим, что x двоичных символов в лучшем случае могут содержать информацию в количестве x бит. Таким образом, при конструировании кода, обнаруживающего и исправляющего одиночную ошибку, следует учесть, что этого можно добиться лишь при значениях x, удовлетворяющих неравенству
х>= log₂(l+m+x), (1.1)
или 2^x-x-1>=m. (1.1а)

Рис. 7 Зависимость нижней границы допустимых значений x от m (сплошная линия) и зависимость относительной избыточности от m (пунктирная линия).

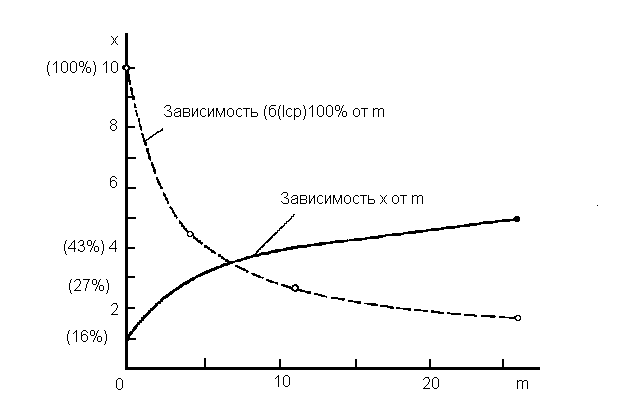
Р. Хэмминг разработал конкретную конструкцию кода. которая обеспечивает весьма элегантное обнаружение и исправление одиночных ошибок при минимально возможном числе дополнительно вводимых двоичных символов, т.е. при знаке равенства в (1.1). Проследим за построением этого кода, когда m = 4. Из рисунка следует, что при этом допустимое значение x равно трем, т.е. при числе основных (информационных) двоичных символов m = 4, число дополнительно введенных, т.е. контрольных символов должно быть не менее трех. Примем, что нам удалось "обойтись" именно тремя дополнительными символами, т.е. удалось сконструировать такой код, при котором каждый из дополнительно введенных трех символов дает нам максимально возможное количество информации, т.е. по одному биту. Тогда в расширенном кодовом наборе окажутся семь двоичных символов:

B1B2B3B4 B5B6B7

(информационные символы) (контрольные символы)

 

Поскольку символы B1 - B4 заняты кодированием собственно текста, то управлять их значениями нам не дано. Что же касается символов B5 - B7, то они предназначены именно для обнаружения и исправления ошибок и поэтому их значения мы можем увязать со значениями информационных символов произвольными тремя функциями от аргументов B1 - B4:

B5=B5(B1,...,B4) (1.11)
B6=B6(B1,...,B4) (1.12)

B7=B7(B1,...,B4) (1.13)

такими, чтобы в последующем с помощью трех других функций от аргументов B1 - B7

e₀=e₀(B1-B7) (1.14)

 

e₁=e₁(B1-B7) (1.15)

 

e₂=e₂(B1-B7) (1.16)

определить значения e₀,e₁,e₂ содержащие информацию о том, произошла ли ошибка вообще и если да, то на уровне какого именно из семи символов. Очевидно, имеется множество различных вариантов при выборе функций (1.11)- (1.16). Р. Хэмминг поставил перед собой задачу выбора именно такой совокупности функций (1.11) - (1.16), чтобы набор значений e₂e₁e₀ оказался двоичной записью позиции, где произошла ошибка. В случае же, когда ошибка не имела места, набор e₂e₁e₀ должен указать на нулевую позицию, т.е. на несуществующий символ B0. Из двоичной записи этих позиций

000 (0) 1 0 0 (4)

001 (1) 1 0 1 (5)

010 (2) 1 1 0 (6)

011 (3) 1 1 1 (7)

легко уследить, что значение e₀ "несет ответственность" за позиции B1, B3, B5 и B7 и поэтому в качестве функции (1.14) берется зависимость

e₀ = B1+B3+B5+B7 mod 2. (1.14а)

Аналогично, обращая внимание на то, что значения e₁ и e₂ отвечают за соответственно B2 B3 B6 B7, B4 B5 B6 B7, получим

e₁= B2+B3+B6+B7 mod 2, (1.15a)

e₂= B4+B5+B6+B7 mod 2. (1.16a)

Обратим внимание, что систему (1.14а) - (1.16а) можно рассматривать как развернутую запись матричного уравнения

 

B1

B2

e₀ 1010101 B3

e₁ = 0110011 B4

e₂ 0001111 B5

B6

B7

или
V_e=AV_a,
где V_e, - вектор ошибки, указывающий на ее месторасположение; А - основная матрица, столбцы которой суть двоичные записи чисел от одного до семи.

Операция сложения во всех трех уравнениях (1.14а) - (1.16а) осуществляется по модулю два. Подставляя в систему уравнении (1.14а) - (1.16a) e₀=e₁=e₂=0, получим систему из трех уравнений

B1+B1+B5+B7=0 mod2 (1.14б)

B2+B3+B6+B7=0 mod2 (1.15б)

B4+B5+B6+B7=0 mod2, (1.16б)

 

Приняв в качестве неизвестных величины B5, B6 и B7 получим систему из трех уравнений с тремя неизвестными:

 

B5+B7=B1+B3 mod2, (1.14в)

B6+B7=B2+B3 mod2, (1.15в)

B5+B6+B7=B4 mod2. (1.16в)

Эта система эквивалентна одному матричному уравнению

 

B1

101 B5 1010 B2

011 B6 = 0110 B3 (1.17)

111 B7 0001 B4

 

или

CV_e=IV_i. (1.17a)

где V_e и V_i, векторы-столбцы, координаты которых представлены соответственно контрольными и информационными разрядами; С и I - так называемые контрольная и информационная матрицы. Столбцы этих матриц суть двоичные записи номеров соответственно контрольных и информационных разрядов.

Решение системы (1.14в) - (1.16в), или. что то же самое, матричного уравнения (1.17) относительно B5, B6, B7 приводит к конкретным выражениям для функций (1.11) -(1.13):

B5=B2+B3+B4 mod2, (1.11а)

B6=B1+B3+B4 mod2, (1.12а)

B7=B1+B2+B4 mod2. (1.13a)

Заметим, что сам Р. Хэмминг в качестве контрольного берет не набор символов B(m+1),B(m+2),...B(m+x), а нaбор символов, индексы которых представляют целые степени двойки. В случае, когда число контрольных символов равно трем, эти индексы равны 2⁰ =1, 2¹ = 2 и 2² = 4, т.е. речь идет о наборе символов B1B2B4, относительно которых решение системы (1.14б) - (1.16б) чрезвычайно упрощается:

B1=B3+B5+B7 mod 2,

B2=B3+B6+B7 mod 2,

B4=B5+B6+B7 mod 2.

Это и естественно, поскольку в данном случае вместо (1.17) имеем дело с матричным уравнением

 

B3

1 0 0 B1 B5

0 1 0 B2 = B6

0 0 1 B4 B7

 

где контрольная матрица С всегда равна единичной матрице.

Отметив, что при указанной рекомендации Р. Хэмминга контрольная матрица всегда (независимо от m и x) оказывается равной единице, подробное обсуждение этой рекомендации оставим на потом, продолжая рассматривать в качестве контрольных B5B6B7 а качестве информационных - B1B2B3B4.

Рассмотрим, к примеру, набор информационных символов B1B2B3B4 = 1011. С помощью зависимостей (1.11a) - (1.13а) определим набор контрольных (дополнительно введенных, избыточных) символов B5B6B7 = 010. Пусть ошибка произошла на уровне символа B5 т.е. вместо истинного расширенного кодового набора 1011 (0)10 получен код 1011 (1)10. Тогда с помощью зависимостей (1.14а)- (1.16а) найдем

e₀=1+1+1+0=1 mod2,

e₁=0+1+1+0=0 mod2,

e₂=1+1+1+0=1 mod2.

Набор значений e₂e₁e₀=101 является двоичной записью числа "пять", т.е. указывает именно на пятую позицию (на символ B5), где, собственно, и произошла ошибка.

Приведенная схема Р. Хэмминга по конструированию кода, обнаруживающего и исправляющего одиночную ошибку, универсальна, и аналогичный код может быть построен для произвольной пары значений m и x, удовлетворяющих уравнению

2^х- х - 1 = m. (1.10б)

Заметим также, что вовсе не обязательно, чтобы набор из m информационных символов представлял собой код какой-то определенной буквы, как это имело место в только что рассмотренном примере. На практике сначала можно осуществить оптимальное (или близкое к оптимальному) кодирование текста. Затем уже закодированный текст можно делить на блоки по m двоичных символов в каждом, причем из возможных значений m = 2^x - х - 1 (х = 3, 4,...) его конкретное значение следует выбирать исходя из эксплуатационной необходимости. При прочих равных условиях значение m должно быть тем меньшим, чем больше значимость информации и чем больше уровень помех. После выбора конкретного значения m каждый блок из m информационных символов следует наращивать х = х (m) контрольными символами, предназначенными для обнаружения и исправления одиночных ошибок в рамках данного блока.

А теперь вернемся к рассмотрению вопроса о том, почему Р. Хэмминг в качестве контрольных берет именно символы, индексы которых равны целым степеням двойки, т.е. 1, 2, 4, 8, 16,.... Во-первых, как уже об этом говорилось выше, при таком выборе контрольная матрица всегда оказывается равной единице, т.е. фактически снимается вопрос решения системы (1.14б)-(1.16б) относительно контрольных символов, так как ее "решение" сводится к простому переписыванию соответствующих уравнений. Но это не главное, так как систему (1.14б)-(1.16б) приходится решать только один раз и далее при каждом акте кодирования мы пользуемся лишь системой (1.11a) - (1.1 За) - решением системы (1.14б)-(1.16б) относительно контрольных символов. При реализации процедур кодирования и декодирования на ЭВМ сам факт, что контрольные символы разобщены (не следуют подряд друг за другом), создает определенные неудобства при каждом акте кодирования и декодирования. Естественно поэтому желание выбрать контрольные символы таковыми, чтобы они следовали подряд друг за другом, пусть даже ценою того, чтобы один раз решить систему (1.14б) - (1.16б). Именно так поступали мы, когда вопреки рекомендации Р. Хэмминга взять в качестве контрольных символы B1,B2 и B4 взяли в качестве таковых символы B5, B6 и B7. Хотя это и вынудило нас решить систему (1.14в) - (1.16в) относительно переменных B5, B6 и B7, но зато при каждом акте кодирования и декодирования мы смогли оперировать "пачками" контрольных символов, а не "выковыривать" их среди информационных символов.

Возникает вопрос; а всегда ли, при любом числе информационных символов мы смогли бы поступать аналогичным образом? Нет, не смогли бы, если по-прежнему хотим, чтобы двоичный набор символов e_x-1,e_x-2,...,e₀ указывал на адрес ошибки. Потому что уже когда число контрольных символов больше трех, мы не имеем права взять в качестве контрольных последние х символов. Легко убедиться, что при этом контрольная матрица непременно оказалась бы вырожденной, т.е. значение ее детерминанта оказалась бы равным нулю. Более того, даже в рассмотренном нами случае, когда число контрольных символов равно трем, мы не смогли бы в качестве контрольных взять, например, первые три символа. Во всех этих случаях определители контрольных матриц (вспомним, что столбцы этой матрицы суть двоичные записи номеров выбранных нами контрольных символов) оказываются равными нулю. Пусть, например, мы выбрали в качестве контрольных не пачку символов B5, B6, B7, а символы B1, B2, B3. Тогда нам пришлось бы иметь дело с квадратной матрицей третьего порядка, столбцы которой являются двоичными формами записи чисел 1, 2 и 3:

С = 011.

Равенство нулю детерминанта этой матрицы свидетельствует о том, что систему (1.14б) - (1.16б) нельзя решить относительно переменных B1, B2, B3.

Таким образом, при выборе среди m + x символов x контрольных следует заботиться о том, чтобы определитель контрольной матрицы порядка x, столбцы которой представляют собой двоичные записи номеров выбранных символов, не оказался равным нулю. Именно чтобы избавиться от этих забот, Р. Хэмминг рекомендует в качестве контрольных взять символы с индексами I, 2, 4, 8 и т.д. Легко обнаружить, что при таком выборе контрольных символов мы всегда (независимо от их числа) будем иметь дело с единичной матрицей.

Кроме зависимости (1.10а). на рисунке приведена также зависимость относительной избыточности от m. Легко заметить, что с увеличением m требуемый процент избыточности для обнаружения и исправления одиночной ошибки резко уменьшается. Столь неестественный результат является следствием искусственного, далекого от реальности допущения, что в рамках каждого кодового набора независимо от его длины m + x может произойти не более одной ошибки. Если же допустить возможность двух и более ошибок, то задача их обнаружения, и тем более исправления усложняется. Построить для этих случаев коды столь же элегантные, как код Р. Хэммннга для одиночной ошибки, пока не удалось.

 

Военная академия Ракетных войск стратегического назначения

имени Петра Великого

 

Кафедра №24

 

ЛЕКЦИЯ №10 «КРИПТОГРАФИЧЕСКИЕ МЕТОДЫ ЗАЩИТЫ ИНФОРМАЦИИ»

 

ПО УЧЕБНОЙ ДИСЦИПЛИНЕ: « ИНФОРМАЦИОННЫЕ СЕТИ И ТЕЛЕКОММУНИКАЦИИ»

 

Автор(ы ): Баричев С.Г., КТН, старший преподаватель;

 

Рассмотрено и одобрено на заседании кафедры (ПМК кафедры)

Протокол № ___ от «___» _______ 2008 г.

МОСКВА 2008

Лекция 10

Тема: Криптографические методы защиты информации

Вопросы:

1) Основные термины и определения

2) Требования к современным шифрам

1. Основные понятия и определения криптографии

 

Итак, криптография дает возможность преобразовать информацию таким образом, что ее прочтение (восстановление) возможно только при знании ключа.

Перечислю вначале некоторые основные понятия и определения.

Алфавит - конечное множество используемых для кодирования информации знаков.

Текст - упорядоченный набор из элементов алфавита.

В качестве примеров алфавитов, используемых в современных ИС можно привести следующие:

алфавит Z₃₃ - 32 буквы русского алфавита и пробел;

алфавит Z₂₅₆ - символы, входящие в стандартные коды ASCII и КОИ-8;

бинарный алфавит - Z₂ = {0,1};

восьмеричный алфавит или шестнадцатеричный алфавит;

Шифрование - преобразовательный процесс: исходный текст, который носит также название открытого текста, заменяется шифрованным текстом.

Дешифрование - обратный шифрованию процесс. На основе ключа шифрованный текст преобразуется в исходный.

Ключ - информация, необходимая для беспрепятственного шифрования и дешифрования текстов.

Криптографическая система представляет собой семейство T преобразований открытого текста. xлены этого семейства индексируются, или обозначаются символом k; параметр k является ключом. Пространство ключей K - это набор возможных значений ключа. Обычно ключ представляет собой последовательный ряд букв алфавита.

Криптосистемы разделяются на симметричные и с открытым ключом (или асимметричесские).

В симметричных криптосистемах и для шифрования, и для дешифрования используется один и тот же ключ.

В системах с открытым ключом используются два ключа - открытый и закрытый, которые математически связаны друг с другом. Информация шифруется с помощью открытого ключа, который доступен всем желающим, а расшифровывается с помощью закрытого ключа, известного только получателю сообщения.

Термины распределение ключей и управление ключами относятся к процессам системы обработки информации, содержанием которых является составление и распределение ключей между пользователями.

Электронной (цифровой) подписью называется присоединяемое к тексту его криптографическое преобразование, которое позволяет при получении текста другим пользователем проверить авторство и подлинность сообщения.

Криптостойкостью называется характеристика шифра, определяющая его стойкость к дешифрованию без знания ключа (т.е. криптоанализу). Имеется несколько показателей криптостойкости, среди которых:

количество всех возможных ключей;

среднее время, необходимое для криптоанализа.

 

Преобразование T_k определяется соответствующим алгоритмом и значением параметра k. Эффективность шифрования с целью защиты информации зависит от сохранения тайны ключа и криптостойкости шифра.

Процесс криптографического закрытия данных может осуществляться как программно, так и аппаратно. Аппаратная реализация отличается существенно большей стоимостью, однако ей присущи и преимущества: высокая производительность, простота, защищенность и т.д. Программная реализация более практична, допускает известную гибкость в использовании.

Для современных криптографических систем защиты информации сформулированы следующие общепринятые требования:

зашифрованное сообщение должно поддаваться чтению только при наличии ключа;

 

число операций, необходимых для определения использованного ключа шифрования по фрагменту шифрованного сообщения и соответствующего ему открытого текста,

должно быть не меньше общего числа возможных ключей;

 

число операций, необходимых для расшифровывания информации путем перебора всевозможных ключей должно иметь строгую нижнюю оценку и выходить за пределы возможностей современных компьютеров (с учетом возможности использования сетевых вычислений);

 

знание алгоритма шифрования не должно влиять на надежность защиты;

 

незначительное изменение ключа должно приводить к существенному изменению вида зашифрованного сообщения даже при использовании одного и того же ключа;

 

структурные элементы алгоритма шифрования должны быть неизменными;

 

дополнительные биты, вводимые в сообщение в процессе шифрования, должен быть полностью и надежно скрыты в шифрованном тексте;

 

длина шифрованного текста должна быть равной длине исходного текста;

 

не должно быть простых и легко устанавливаемых зависимостью между ключами, последовательно используемыми в процессе шифрования;

 

любой ключ из множества возможных должен обеспечивать надежную защиту информации;

алгоритм должен допускать как программную, так и аппаратную реализацию, при этом изменение длины ключа не должно вести к качественному ухудшению алгоритма шифрования.

Основные современные методы шифрования

 

Среди разнообразнейших способов шифровании можно выделить следующие основные методы:

• Алгоритмы замены или подстановки — символы исходного текста заменяются на символы другого (или того же) алфавита в соответствии с заранее определенной схемой, которая и будет ключом данного шифра. Отдельно этот метод в современных криптосистемах практически не используется из-за чрезвычайно низкой криптостойкости.

• Алгоритмы перестановки — символы оригинального текста меняются местами по определенному принципу, являющемуся секретным ключом. Алгоритм перестановки сам по себе обладает низкой криптостойкостью, но входит в качестве элемента в очень многие современные криптосистемы.

• Алгоритмы гаммирования — символы исходного текста складываются с символами некой случайной последовательности. Самым распространенным примером считается шифрование файлов «имя пользователя.рwl», в которых операционная система Microsoft Windows 95 хранит пароли к сетевым ресурсам данного пользователя (пароли на вход в NT-серверы, пароли для DialUр-доступа в Интернет и т.д.). Когда пользователь вводит свой пароль при входе в Windows 95, из него по алгоритму шифрования RC4 генерируется гамма (всегда одна и та же), применяемая для шифрования сетевых паролей. Простота подбора пароля обусловливается в данном случае тем, что Windows всегда предпочитает одну и ту же гамму

• Алгоритмы, основанные на сложных математических преобразованиях исходного текста по некоторой формуле. Многие из них используют нерешенные математические задачи. Например, широко используемый в Интернете алгоритм шифрования RSA основан на свойствах простых чисел.

• Комбинированные методы. Последовательное шифрование исходного текста с помощью двух и более методов.

 

Требования к современным шифрам

1. Размер блока должен быть равен 128 бит. Хотя размер блока в 64 бита и считается в настоящее время вполне надежным, однако быстрый прогресс микроэлектроники уже в обозримом будущем может сделать его доступным для некоторых типов словарных атак. Кроме того, при построении хэш-функций на базе блочных шифров в силу так называемого "парадокса дней рождения" весьма желательно, чтоб размер блока использованного шифра был как минимум вдвое больше величины, считающейся на данный момент безопасной. В свете этого выбор большего размера блока представляется вполне разумным.

2. Шифр должен допускать использование ключа размером 256, 192 и 128 бит. Шифры первого поколения создавались в основном для нужд государства. В настоящее время одним из главных потребителей средств криптозащиты информации (СКЗИ) становится бизнес, который, как известно, любит считать деньги и не хочет их тратить больше, чем необходимо. В различных задачах деловой сферы требования к надежности СКЗИ сильно различаются. Поскольку стоимость разработки и эксплуатации СКЗИ существенно возрастает с увеличением их надежности, нередко экономические соображения диктуют выбор более слабых криптографически, но зато более дешевых средств шифрования. В свете сказанного у бизнеса возникла необходимость не в одном шифре, а в целой линейке шифров, которые различались бы по своим рабочим характеристикам, что нашло отражение в наборе требований к кандидатам на место усовершенствованного стандарта, - они должны допускать использование ключей различных размеров.

3. Стойкость шифра не должна быть ниже, чем у тройного DES. В настоящее время этот шифр считается вполне надежным даже с некоторым запасом на возможный прогресс криптоанализа в ближайшем будущем.

4. Быстродействие возможных программных реализаций должно быть не ниже, чем у тройного DES. Это также вполне понятное требование, - было бы неразумно принять в качестве нового стандарта шифр с худшим показателем, чем у действующего ныне варианта.

5. Шифры должны допускать возможность эффективной реализации различных типов, - аппаратной и программной на процессорах всего диапазона от 8-битовых микроконтроллеров до современных 64-разрядных процессоров. Это требование диктуется сферой бизнеса, т.к. предполагается интенсивное использование нового стандарта в широком спектре изделий - от интеллектуальных карт и модемов до специальной аппаратуры и реализаций на супер-ЭВМ.

В качестве кандидатов на место нового стандарта различные организации, компании и частные лица выдвинули 15 перечисленных ниже шифров:
CAST-256, CRYPTON, DEAL, DFC, E2, HPC, FROG, LOOKI-97, MAGENTA, MARS, R6, RIJNDAEL, SAFER+, SERPENT, TWOFISH.
Большинство из них разработаны в последние несколько лет и отражают, таким образом, новейшие достижения рассматриваемой области криптографии. Ниже в таблице 1 дан краткий обзор по ключевым моментам архитектуры этих шифров

Если в ранних шифрах для преобразования данных использовался достаточно ограниченный набор операций, - битовые перестановки, подстановки в битовых группах и аддитивные бинарные операции, - то в современных шифрах этот круг несколько шире. Что касается битовых перестановок общего вида, то они встречаются только в самых ранних шифрах ("Люцифер", DES) и не применяются на практике уже достаточно долгое время. Это обусловлено их крайне неэффективной реализацией на современных универсальных процессорах. Вместо них получили широкое распространение согласованные битовые перестановки - вращения, перестановки целых групп разрядов, и перестановки, реализуемые за несколько логических операций над преобразуемыми словами данных.

Узлы замен в ранних шифрах отличались небольшим размером заменяемого элемента, - 4-6 бит, - и конструировались с помощью специальных закрытых методик. В большинстве современных шифров размер узла составляет не меньше 8 бит. Кроме того, критерии проектирования узлов открыты и при их конструировании широко используется алгебраический подход:

в SAFER+ байтовые узлы замен сконструированы на базе экспоненты и логарифма в конечном поле небольшого размера (операции выполняются по модулю 257).

в RIJNDAEL единственный байтовый узел замен задается следующим уравнением, оперирующим элементами конечного поля GF(2⁸):

S[X] = (x⁷+x⁶+x²+x) + X^-1 (x⁷+x⁶+x⁵+x⁴+1) mod (x⁸+1),

где X^-1 - мультипликативное обращение байта X в конечном поле GF(2⁸) по модулю неприводимого полинома

m(x) = x⁸+x⁴+x³+x+1,

при этом полагают 0^-1=0.

в LOKI-97 используются два разноразмерных узла замен, определяемых следующими алгебраическими соотношениями:

S₁[x]=(x³ mod 2911₁₆) mod 2⁸, 0 x<2¹³,
S₂[x]=(x³ mod AA7₁₆) mod 2⁸, 0 x<2¹¹.

Кроме того, в некоторых современных шифрах (BLOWFISH, FROG) узлы замен зависят от используемого ключа и формируются динамически во время выработки последовательности ключевых элементов для раундов шифрования. В целом, в настоящее время наблюдается гораздо большее