Проблема обеспечения безопасности в корпоративном облачном хранилище

Поскольку система SMART представляет собой корпоративную облачную инфраструктуру, возникает проблема обеспечения контроля доступа пользователей, а также их авторизации.

Корпоративное хранилище данных отличается от «обычных» облачных хранилищ, таких как Dropbox или Google Drive, тем, что в последних пользователь сам создаёт себе хранилище и заполняет его своими данными, доступ к которым по умолчанию имеет только он, однако он может предоставлять доступ и другим пользователям. Корпоративное облако представляет собой одно централизованное хранилище, в котором хранятся данные всех пользователей (например, сотрудников предприятия), но доступ к которым имеет только определённый круг лиц с соответствующими правами в зависимости от степени секретности хранимой информации. Управлением доступа и назначением прав пользователя занимается администратор.

В рамках данной главы были проведены теоретические исследования проблемы обеспечения надёжного контроля доступа с помощью изучения различной технической литературы – книг, научных статей.

В процессе исследования работы [1] был сделан вывод, что наиболее подходящим механизмом для обеспечения контроля доступа в корпоративном облаке является система шифрования на основе атрибутов (ABE), поскольку именно набор атрибутов пользователя и файлов описывают права (политику) доступа к этим файлам и выполнения над ними определённых операций. Также в этой работе описано, что пользователь, который является владельцем секретной информации и помещает эту информацию в хранилище, может сам задавать политику доступа к этому файлу, т. е. по сути некоторый набор атрибутов на основе специфических данных, лежащих в основе скрываемой информации. Более того, этот пользователь может не знать точной персональной информации о других лицах, которым доступны скрываемые данные, но владелец информации должен иметь способ описать получателей в рамках описательных атрибутов и полномочий.

ABE-система также поддерживает механизм аутентификации, поскольку необходимо удостовериться, что пользователь получил ключи именно от доверенного центра (администратора). Предшественник ABE – система шифрования на основе идентификаторов – не обладала механизмом, отвечающим за контроль доступа, поэтому была улучшена в работе Амита Сахаи (Amit Sahai) и Брента Уотерса (Brent Waters) [3]. Они же и ввели понятие шифрования на основе атрибутов.

В работе [6] рассмотрены основные критерии, которым должна удовлетворять система на основе атрибутов. Их 6:

- Конфиденциальность данных. Данные должны быть зашифрованы владельцем перед отправкой их в облако. Участники, которые не прошли авторизацию, не могут узнать о данных, которые были зашифрованы.

- Детальный контроль доступа. В группе пользователей для каждого отдельно взятого участника группы система предоставляет различные правила доступа. Таким образом, пользователи, которые находятся в одной группе, могут иметь различные правила доступа к данным.

- Масштабируемость. Число зарегистрированных пользователей не должно влиять на производительность системы.

- Контроль действий. Недопустима передача атрибутов секретного ключа авторизованного пользователя другим лицам.

- Отзыв прав пользователя. Если пользователь выходит из системы, то система может отозвать права данного пользователя. Пользователь, чьи права были отозваны, уже не сможет получить доступ к данным.

- Невозможность сговора. Пользователи не могут объединять свои атрибуты, чтобы расшифровать данные, поскольку каждый атрибут связан с многочленом или случайным числом. Таким образом, пользователи не могут вступать в сговор друг с другом.

Постановка задачи

В рамках данной работы поставлены следующие задачи:

- рассмотреть классический алгоритм шифрования на основе атрибутов (ABE);

- построить модификацию алгоритма ABE, которая будет удовлетворять 6 вышеописанным критериям;

- разработать архитектуру системы защиты и контроля доступа, определить основные компоненты;

- выбрать программные средства для реализации прототипа данной системы;

- разработать и протестировать прототип и оценить полученные результаты, представить соответствующие графики, оценить полученные результаты и сделать вывод о применимости данной системы в облачных инфраструктурах малых и средних предприятий, в том числе в системе SMART.

Выводы

В данной главе были получены следующие результаты:

- рассмотрены основные термины и определения, используемые в рамках данной работы;

- исследованы проблемы обеспечения безопасности в корпоративных облачных инфраструктурах;

- поставлены основные задачи.

 

ГЛАВА 2. МОДЕЛИ И АЛГОРИТМЫ

Эллиптические кривые

Алгоритм ABE на этапе генерации ключей использует эллиптические кривые, которые необходимы для построения билинейного преобразования.

Билинейное преобразование – это преобразование, которое имеет следующий вид:

 

φ: G1 × G1 → G2

(2.1)

 

Здесь G₁ и G₂ – мультипликативные циклические группы простого порядка p.

Преобразование обладает следующими полезными свойствами:

- билинейность: ∀u, v ∈ G₁; a, b ∈ Z_p: φ(u^a,v^b) = φ(u,v)^ab;

- невырожденность: φ(g, g) ≠ 1.

Эллиптическая кривая – множество точек, которые описываются следующим уравнением:

y^2 = x^3 + ax^2 + bx + c

(2.2)

 

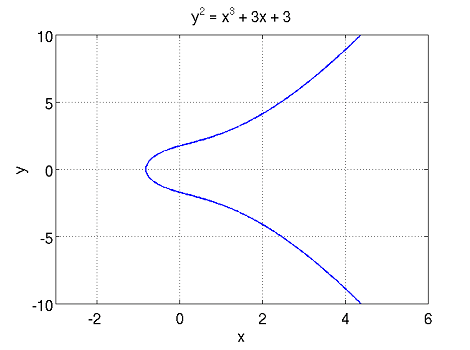
Т. е. эллиптическая кривая – это кривая третьей степени, либо кубическая кривая.

На рисунке ниже изображён график одной из эллиптических кривых:

 

 

Рисунок 2.1 Пример эллиптической кривой

Проблема применения эллиптических кривых в криптографии представлена в работе [10].

В криптографии не применяются эллиптические кривые над вещественными или комплексными полями, поскольку в данном случае возникает проблема округления, т. е. используя, например, эллиптические кривые над вещественными числами, мы не сможем получить биекцию между исходным текстом и зашифрованными данными. Поэтому следует применять только кривые над конечными полями, т. е. таким кривым принадлежат точки из конечного поля.

Криптография рассматривает два вида эллиптических кривых (ЭК):

- ЭК над конечным полем Z_p простого порядка p (оно же и кольцо вычетов по модулю p);

- ЭК над бинарным конечным полем GF(2^m).

Точка эллиптической кривой над конечным полем представляет собой группу, для которой определена операция сложения.

Пусть есть 2 точки ЭК A(x_a, y_a) и B(x_b, y_b). Тогда сумма этих точек вычисляется следующим образом:

xA+B = α^2 – xb – xa yA+B = -yb + α(xa – xb)

(2.3)

Графически сложение двух точек выглядит следующим образом:

Рисунок 2.2 Сложение двух точек эллиптической кривой

Для сложения точек P и Q, необходимо провести между ними прямую линию, которая обязательно пересечет кривую в какой-либо третьей точке R. Отразим точку R относительно горизонтальной оси координат и получим искомую точку P+Q.

Эллиптические кривые над полем GF(2^m) обладают одним очень важным преимуществом: элементы этого поля можно легко представить в виде n-битных кодовых слов, что увеличивает скорость аппаратной реализации алгоритмов, основанных на ЭК.

Все математические операции на эллиптических кривых над конечным полем производятся в соответствии со свойствами конечного поля, над которым построена эллиптическая кривая. Т.е. для вычисления, например, суммы двух точек кривой E над кольцом вычетов все операции производятся по модулю числа p.

В случае использования бинарного поля возникает проблема при сложении двух одинаковых элементов, т. е. в результате сумма их равна 0. Характеристика такого поля равна 2, т. к. 0 ⊕ 0 = 0 и 1 ⊕ 1 = 0. Поэтому над данным полем необходимо использовать ЭК следующего вида:

 

y^2 + xy = x^3 + ax^2 + b, b ≠ 0

(2.4)

 

Существуют различные атаки на эллиптические кривые:

- алгоритм Шенкса;

- алгоритм Полига-Хеллмана (алгоритм решения дискретного логарифма).

Основные преимущества ЭК:

- возможность использования ключа небольшой длины (в отличие от «классической» асимметрической криптографии);

- скорость работы алгоритмов, построенных на эллиптических кривых, намного больше, чем у классических асимметрических алгоритмов (например, RSA), поскольку ускорение достигается за счёт использования структуры бинарного конечного поля;

- эффективное использование ограниченных вычислительных ресурсов ввиду небольшой длины ключа и высокой скорости работы.

Основные недостатки ЭК:

- сложность в изучении, что увеличивает вероятность возникновения различных уязвимостей и ошибок при разработке систем;

- все преимущества использования эллиптической криптографии основаны на одном основном факте: не существует субэкспоненциальных алгоритмов решения задачи дискретного логарифмирования на эллиптических кривых, что позволяет уменьшить длину ключа, тем самым увеличив производительность. Однако появление таких алгоритмов означает бесполезность применения эллиптической криптографии.