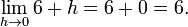Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: вступ до математичного аналізуСодержание книги
Поиск на нашем сайте
1)Дослідження властивостей основних геометричних функцій. 2)Точки розриву функцій та їх класифікація.
Неперервність функції
Означення Функція 1) вона визначена в цій точці і в деякому її околі; 2) нескінченно малому приростові аргументу відповідає нескінченно малий приріст функції:
Приклад. Дослідити на неперервність функцію Розв’язання.
Якщо
Неперервність функції в точці можна означити і по-іншому. Означення. Функція
Рівність можна деталізувати: границя зліва в точці
Означення. Функція
Арифметичні операції над неперервними функціямиприводять знову до неперервних функцій. Теорема. Якщо функції
1)
2)
3)
Доведення. Нехай функції
1)
2)
3) Бачимо, що означення 2.9 виконується в кожному з цих випадків. Тобто ми показали, що при виконанні арифметичних дій над неперервними функціями ми знову отримаємо неперервні функції.
Неперервність складеної функції
Теорема. Якщо функція Доведення. Справді, оскільки функція
Самостійна робота №5. Тема: Диференціальне числення функції однієї змінної. 1. Похідні вищих порядків та їх застосування. 2. Похідні функцій, заданих неявно та параметрично 3. Найбільше та найменше значення функції на відрізку
Нехай в деякому околі точки x0 визначена функція f. Якщо ми візьмемо довільне число x в цьому околі, то приріст аргументу (позначається Δx) в цьому випадку визначається, як x−x0, а приріст функції (Δy) — як f(x)−f(x0). Тоді, якщо існує границя Похідною функцією даної функції називається функція, що в будь-якій точці області визначення дорівнює похідній даної функції в цій точці.
Диференціювання – це метод обчислення співвідношення приросту залежної змінної y по відношенню до приросту незалежної змінної x. Це співвідношення приростів називається похідною функції y по змінній x. Якщо говорити більш точно, залежність y від x означає, що y функція від x. Ця функціональна залежність часто позначається y = ƒ (x), де ƒ позначає функцію. Якщо x та y дійсні числа, і якщо графік функції y зображено відносно x, похідна дорівнюєнахилу дотичної до цього графіка в кожній точці. Найпростіший випадок коли y – лінійна функція від x, це означає що графік функції y відносно x пряма лінія. В такому випадку, y = ƒ (x) = m x + b, для дійсних чисел m та b, і нахил m визначається так
де символ Δ (грецька літера у верхньому регістрі дельта) – це є скорочення для "зміни в". Ця формула справедлива тому, що y + Δ y = ƒ (x + Δ x) = m (x + Δ x) + b = m x + b + m Δ x = y + m Δ x. З цього випливає, що Δ y = m Δ x. Отримали точне значення нахилу прямої лінії. Якщо функція ƒ не лінійна (тобто графік функції не пряма лінія), тоді приріст y поділений на приріст x змінюється: диференціювання це спосіб обчислення точного значення відношенння приростів для будь-якого значення x.
Пояснення визначення Нехай ƒ – функція дійсних чисел. В класичній геометрії, дотична до графіка функції ƒ для дійсного числа a була єдина лінія через точку (a, ƒ (a)), що не перетинається з графіком функції ƒ трансверсально, це означає що ця лінія не проходить крізь графік. Похідна функції y по змінній x в точці a, з геометричної точки зору, це нахил дотичної лінії до графіка функції ƒ в точці a. Нахил дотичної дуже близький до нахилу лінії, що проходить крізь точку (a, ƒ (a)) та іншу близьку точку на графіку, наприклад(a + h, ƒ (a + h)). Такі лінії називаються січними. Значення h близьке до нуля дає добре наближення для нахилу дотичної, а чим менше значення h, в загальному випадку, тим краще буде наближення. Нахил m січної лінії дорівнює різниці значень y для цих точок поділити на різницю значень x, тобто
Цей вираз — це відношення приростів Ісаака Ньютона. Похідна — це значення відношення приростів у випадку коли січні лінії наближаються до дотичної. Строго кажучи, похідна функції ƒ в точці a цеграниця:
відношення приростів коли h наближається до нуля, якщо така границя існує. Якщо границя існує тоді ƒ – диференційована в точці a. Тут ƒ ′ (a) одне з кількох можливих позначень похідної (див. нижче) Запишемо еквівалентний вираз, для похідної справедлива рівність
що також піддається інтуїтивному розумінню (див. рис.1), де дотична лінія ƒ в точці a дає найкраще лінійне наближення
для ƒ біля точки a (наприклад, для малих h). Якщо підставити 0 замість h у відношеня приростів то отримаємо ділення на нуль, отже нахил дотичної лінії не можна обчислити таким способом. Натомість запишемо Q (h), відношення приростів як функцію від h:
Q (h) – це нахил січної лінії між точками (a, ƒ (a)) and (a + h, ƒ (a + h)). Якщо ƒ – неперервна функція, тобто якщо графік функції немає розривів, тоді Q також непервна функція починаючи з точки h = 0. Якщо існує границя На практиці, існування непервного продовження відношення приростів Q (h) в точці h = 0 показують по-іншому: міняють чисельник таким чином щоб скоротити h у знаменнику. Цей прроцес може бути довгим та нудним для складних функцій, тож в таких випадках використовують багато спрощень. Приклад Квадратна функція ƒ (x) = x ² — диференційована в точці x = 3 і її похідна в цій точці дорівнює 6. Цього результату можна досягнути, якщо обчислити границю відношення приростів ƒ (3) при h прямує до нуля:
Тепер можемо обчислити границю, якщо підставимо замість h нуль:
Отже, нахил графіку квадратної функції в точці (3, 9) дорівнює 6, а її похідна в точці x = 3 дорівнює ƒ '(3) = 6. Узагальнюючи, якщо провести схожі обчислення то отримаєм, що квадратна функція в точці x = a дорівнює ƒ '(a) = 2 a.
Самостійна робота №8.
|
||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 232; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.116.50 (0.009 с.) |

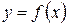 називається неперервною в точці
називається неперервною в точці 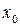 (continuous function at point), якщо:
(continuous function at point), якщо: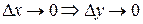 , або
, або  .
.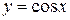 в точці
в точці 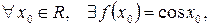
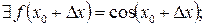

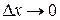 , то
, то  ;
; 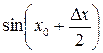 - величина обмежена, тому, за теоремою 2.4,
- величина обмежена, тому, за теоремою 2.4, 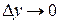 . Отже,
. Отже,  , і тому, за означенням 2.8, функція
, і тому, за означенням 2.8, функція 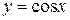 - неперервна в точці
- неперервна в точці 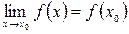 .
.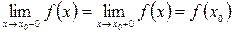 .
.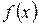 і
і 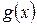 є неперервними в точці
є неперервними в точці 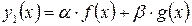 ,
, 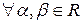 ;
; ;
;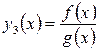 за додаткової умови
за додаткової умови 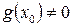 .
.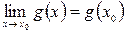 . Використаємо теореми про арифметичні операції над функціями, що мають границю:
. Використаємо теореми про арифметичні операції над функціями, що мають границю: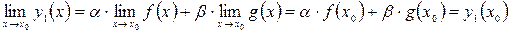 ;
;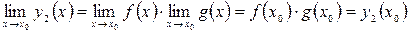 ;
; .
.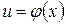 неперервна в точці
неперервна в точці 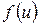 неперервна в точці
неперервна в точці  , то складена функція
, то складена функція  неперервна в точці
неперервна в точці  ;
; 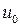 , тому
, тому  . А це означає, що функція
. А це означає, що функція 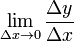 , то вона називається похідною функції f в точці x0.
, то вона називається похідною функції f в точці x0.
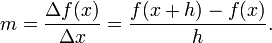


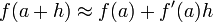
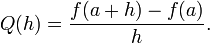
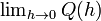 , тобто якщо існує спосіб обчислити значення для Q (0), це означає що графік функції Q неперервний, тоді функція ƒ диференційована в точці a, і її похідна в точці a дорівнює Q (0).
, тобто якщо існує спосіб обчислити значення для Q (0), це означає що графік функції Q неперервний, тоді функція ƒ диференційована в точці a, і її похідна в точці a дорівнює Q (0).