
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Хар-ки типовых динамических звеньев сауСодержание книги Поиск на нашем сайте
Любая АСР(автомат.система регулир.)сост. из элементов или звеньев объединенных в схему при этом Динамич. АСР зависит из динамических хар-к звеньев и сп-бов соединения их в звенья, образующих АСР.Для получ. динамических хар-к всей АСР нужно знать хар-ки всех ее элементов. Объектов регул-ния, датчиков, регуляторов и др. Все элементы АСР по своим динамическим хар-кам, т.е по зав-сти вых. величины -безинерционные (усилительные); -инерционные (аппериодическое звено 1-го порядка); -интегрирующая(астатическое звено 1-го порядка); -дифференцирующие звенья; -колебательно затухающее звено; -аппериодическое звено 2-го порядка; -звено чистого запаздывания. Безинерционное звено (усилителительное). Динамич. хар-тика имеет вид: y=k
Преобразуем ур-ния по Лапласу: y(p)=k Инерционное звено. Динамич. хар-тика такого звена имеет вид: T y =
Для этого (3.2.3)преобразуем по Лапласу:
Одноемкостные статические объекты: термопары, мембрано-исполнительный мех-зм. Данное звено наз-тся аппериодическим звеном 1-го порядка. Интегрирующее звено. Динамич. хар-тика: Т*dy/dt=к*х. Преобразуем: dy/dt=к*х/Т,
y/t=кх/Т=tgα, α=аrctgк*х/Т. Получим функцию звена, преобразуем по Лапласу: Т*р*y(р)=к*х(р), W(р)=y(р)/х(р)=к/Т*р. Данное звено наз-тся астатическим звеном 1-го порядка (емкостные астатические объекты, интегральные регуляторы). Дифференцирующие звенья. делятся на реальные и идеальные. Динамич. хар-ка идеального дифференцирующего звена имеет вид:y=к*dх/dt (При t=0, y
Получим передаточную функцию звена: у(р)=к*р*х(р), W(р)=у(р)/х(р)=к*р Пример:1.Электрический контур, в котором протекает ток и имеется напряжение, тогда ток в контуре будет равен: Динамич. хар-ка реального дифференцирующего звена им вид: Т*dy/dt+y=k*dx/dt (при t=0, y
Получим передаточную функцию: Т*р*у(р)+у(р)=к*р*х(р), W(р)=к*р/(Т*р+1). Пример: электрический контур, содержащий емкость С и сопротивление R. Получим: R*c*Uвых/dt+Uвых= dUвых/dt – з-н Киркгофа. Дифференцирующие звенья широко применяются в АСР и сп-бствует устойчивой ее работе. Колебательное затухающее звено, апериодическое звено 2-го порядка. Это такое звено, у кот. при скачкообразном измен. х, вых. величинана – у изменится в колебательном режиме с постоян. периодом и с амплитудой затухающего колебания по экспоненте. Динамич. хар-ка имеет вид: Т02*d2y/dt2+T*dy/dt+y=к*х. Это ур-ние 2-го порядка, звено имеет 2 емкости – Т0 и Т. Для решения ур-ния надо получить передаточную функцию и хар-терное ур-ние для данного звена. Передаточная функция: Т02*р02*у(р)+Т*р*у(р)+у(р)=к*х(р) W(р)=у(р)/х(р)=к/(Т02*р2+Т*р+1). Хар-терное ур-ние (когда знаменатель=0): Т02*р2+Т*р+1=0. Найдем корни: Р,1,2=-Т/(2*Т02)± у= к*х, с=к*х*(ω0/ω), ω0=1/Т0 – частота свободных колебаний вых. переменной, ψ=arctg(ω/α). Подставив все получим: y=кх*[1 –ω0/ω*е-αt*sin(ω*t+arctg ω/α)]. График переходного проц-сса (х=const):
Пример: двухъемкостные статические объекты, электродвигатели переменного тока (асинхронные). Апериодическое звено 2-го порядка: Динамич. хар-тика данного звена имеет вид: Т02*d2y/dt2+T*dy/dt+y=к*х. Хар-тикческое ур-ние данного звена: Т02*р2+Т*р+1=0. Соотношение постоянных времени имеет следующий вид: Т1>2Т0. Корни хар-тикческого ур-ния будут вещ-венными и отрицат.: Р1,2=-α±γ, α=-Т1/2Т0, γ=
Звено чистого запаздывания. Динамич. его харзика имеет вид: у=х*(t – τ), где τ – время чистого запаздывания. График переходного проц-са:
Хар-тика – величина у на выходе звена = вх величине х, но ч-з время τ. Передаточная функция имеет вид: W(р)=у(р)/х(р)=е-р*τ
ПОГРЕШНОСТИ ИЗМЕРЕНИЙ Абсолютной пог-ю наз отклонение результата измерения X от истинного знач. ХИ измеряемой величины: Δ = X – XИ.. в единицах измеряемой величины и наз-тся абсолютной погрешностью измерения. Относительная погрешность измерения — отношение абсолютной погрешности измерения к истинному значению измеряемой величины: δ= (Δ /XИ )*100% Получаемую оценку погрешности, представляющую собой разность Δ м-ду полученным при измерении и действительным знач.ми физической величины (здесь и далее имеется в виду абс. погрешность), в зав-сти от причин возникновения, хар-тера и условий проявления принято выражать суммой двух составляющих, называемых случайной ψ и систематической q погрешностями измерений: Δ = q + y. Случайная погрешность измерения — составляющая погрешности измерения, изменяющаяся случайным образом при повторных измерениях одной и той же величины,определ.ься факторами кот.проявл.нерегулярно и с разной интенсивностью. Знач. и знак случайной погрешности определ. невозможно, т.к. в каждом опыте причины, вызывающие погрешность, действуют неодинаково. Случайная погрешность всегда есть и не м.б. исключена из результата измерений. Но проведением ряда повторных измерений и исп.для их обработки м-дов математ.статистики опред. знач. измеряемой величины со случайной погрешностью, меньшей, чем при1ом измерения,при этом чаще всего исп.нормальный з-н распределения(Гауса),кот.опр. связь м-ду случайной величиной и вероятностью ее проявления. Для кол-венной оценки случай ной пог-ти при распределении Гауса исп.матем.ожидание Мх и среднеквадратичное отклонение υ.При конечном числе измерений мат.ожиданиеи среднеквадр.отклонение орп.по ф-лам: М(х)=1/n*Σxi, υ= Зав-сть доверительного интервалаот доверительной вероятности выраж.функцией Лопласса,кот.приводят в виде таблицы(Рg втехнолог.измерения обычно приним. 0,95).Иногда случ.пог-ти одного или неск. рез-тов измерений могут сильно отличаться от среднего знач.,их наз.тогда промахами(грубыми погреш-ми).Выявление промаха ведут с исп.статистических м-дов. Систематическая погрешность — составляющая погрешности измерения, остающаяся постоян. или з-номерно изменяющаяся при повторных измерениях одной и той же величины.Ее выявление часто связано с проведением дополнит.исследований. Обнаруженная и оцененная систематическая погрешность исключается из результата введением поправки. В зав-сти от причины возникновения различают след. систематические погрешности: 1.Погрешность м-да (теоретическая погрешность) измерений — составляющая погрешности измерения, обусловленная несовершенством м-да измерений. Здесь необх-мо учитывать тот факт, что м-д измерения, по определению, включает в себя и пр-п измерения. 2. Инструментальная погрешность измерения — составляющая погрешность измерения, зависящая от погрешности применяемых средств измерений. 3. Погрешность установки явл. следствием неправильности установки средств измерений. 4. Погрешность от влияющих величин явл. следствием воздействия на объект и средством измерений внешних факторов (тепловых и воздушных потоков, магнитных, электрических, гравитационных и других полей, атмосферного давления, влажности возд., ионизирующего излучения). 5. Субъективная погрешность обусловлена индивид.свойствами чел.а,кот.пров. измерения. Для обнаружения системат пог-ти исп.средства измерений,основанные на разных м-дах(м-д раидонизации).По хар-теру проявления систематические погрешности делят на постоянные и переменные. Постоянные погрешности не изменяют своего знач. при повторных измерениях. Причинами этих погрешностей явл.: неправильная градуировка или юстировка средств измерений, неправильная установка начала отсчета и т. д. Переменные погрешности при повторных измерениях могут принимать различные знач.. Если переменная погрешность при повторных измерениях возрастает или убывает, то ее наз-ют прогрессивной. Переменная погрешность может изменяться при повторных измерениях периодически или по сложному з-ну. Причинами возникновения переменной систематической погрешности явл.: действие внешних факторов и особенности конструкций средств измерений.
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 344; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.119.119 (0.006 с.) |

 можно классифицировать на след. типовые звенья:
можно классифицировать на след. типовые звенья: x
x
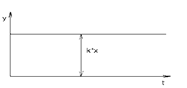
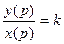 .Пример данного звена- n-регулятор, все усилители,рычаги.
.Пример данного звена- n-регулятор, все усилители,рычаги. (3.2.3),T - постоян. времени, к - коэффициент усиления,x-const;
(3.2.3),T - постоян. времени, к - коэффициент усиления,x-const; (3.2.4). По формуле(3.2.4) построим графики переходного проц-са:
(3.2.4). По формуле(3.2.4) построим графики переходного проц-са:

 ;
;  ;
; 

 ,Проинтегрируем: y-y0=к/Т*
,Проинтегрируем: y-y0=к/Т*  , х=cоnst, y=кх/Т*t+y0. График переходного проц-са:
, х=cоnst, y=кх/Т*t+y0. График переходного проц-са:

 ; при t
; при t  , у=0)
, у=0)

 i=c*dUвых/dt. 2.Трансформеры напряжения: Uвых=к*dФ/dt, Ф=к1*i1 (величина потока создается в сердечнике i1). Uвых=к2*di1/dt (выходное напряжение).
i=c*dUвых/dt. 2.Трансформеры напряжения: Uвых=к*dФ/dt, Ф=к1*i1 (величина потока создается в сердечнике i1). Uвых=к2*di1/dt (выходное напряжение).

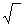 (Т2-4Т02/4*Т04). Данные корни могут быть комплексно-сопряженные или действительно отрицательные. Если Т<2Т0, то корень дифференциала ур-ния будет отрицательным и корни комплексно-сопряженные, т е: Р1,2= - α±j*ω. Коэф-т затухания α=Т/2Т02, ω=
(Т2-4Т02/4*Т04). Данные корни могут быть комплексно-сопряженные или действительно отрицательные. Если Т<2Т0, то корень дифференциала ур-ния будет отрицательным и корни комплексно-сопряженные, т е: Р1,2= - α±j*ω. Коэф-т затухания α=Т/2Т02, ω=  4Т02/Т0/4Т04) – частота вынужденных колебаний вых. величины у. Решение будет иметь вид: у установится у= с*е-αt*sin(ω*t+ψ), где с, ω – постоянные интегрирования, кот. определ. из начальных условий, т е: (dy/dt)t=0. Пар-тры: у установится
4Т02/Т0/4Т04) – частота вынужденных колебаний вых. величины у. Решение будет иметь вид: у установится у= с*е-αt*sin(ω*t+ψ), где с, ω – постоянные интегрирования, кот. определ. из начальных условий, т е: (dy/dt)t=0. Пар-тры: у установится





 . Случайная пог-ть предст.собой интервал наз.доверительным, в кот. с заданной вероятностью Рg попадет в результат измерений.
. Случайная пог-ть предст.собой интервал наз.доверительным, в кот. с заданной вероятностью Рg попадет в результат измерений.


