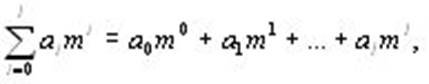Храниться 2k различных целых чисел.

Пример 1. Пусть для представления целых чисел в компьютере используется 16­разрядная

ячейка (2 бай­та). Определить, каков диапазон хранимых чисел, если: а) используются только

положительные числа; б) используются как положительные так и отрицательные числа в равном

количестве. Решение: Всего в 16­разрядной ячейке может храниться 216=65 536 различных

значений. Следовательно: а) Диапазон значений от 0 до 65 535 (от 0 до 2k ­1); Б) Диапазон значений

от ­32 768 до 32 767 (от ­2k-1 до 2k-1­1).

Чтобы получить внутреннее представление целого положительного числа N, хранящегося

в k-разрядном машинном слове, необходимо:

1) перевести число N в двоичную систему счисления;

Полученный результат дополнить слева незначащими нулями до k разрядов

.

Пример 2. Получить внутреннее представление целого положительного числа 1607 в 2­байтовой

Ячейке.

Решение. N = 160710 = 110010001112. Внутреннее представление этого числа в ячейке будет

Следующим: 0000 0110 0100 0111. Шестнадцатеричная форма внутреннего представления числа

получается заменой 4­х двоичных цифр одной шестнадцатеричной цифрой: 0647.

Для записи внутреннего представления целого отрица-тельного числа (-N) необходимо:

1) получить внутреннее представление положитель-ного числа N;

2) получить обратный код этого числа заменой 0 на 1 и 1 на 0;

К полученному числу прибавить 1.

Данная форма представления целого отрицательного числа называется дополнительным кодом.

Использование дополните­льного кода позволяет заменить операцию вычитания на опера­цию

Сложения уменьшаемого числа с дополнительным кодом вычитаемого.

Пример 3. Получить внутреннее представление целого отрицательного числа ­1607.

Решение. 1) Внутреннее представление положительного числа:

0000 0110 0100 0111

2)

обратный код:

1111 1001 1011 1000

3)

Результат прибавления 1: 1111 1001 1011 1001 — это внутреннее двоичное

представление числа ­1607. Шестнадцате­ричная форма: F9B9.

Двоичные разряды в ячейке памяти нумеруются от 0 до k справа налево. Старший, k-й разряд во

Внутреннем представлении любого положительного числа равен нулю, отрицательного числа —

Единице. Поэтому этот разряд называется знаковым разрядом.

Системы счисления. Основные понятия (базис, алфавит, размерность алфавита и др.) Перевод чисел из одной системы счисления в другую.

Системы счисления

 

Для удобства последующего преобразования дискретный сигнал подвергается кодированию (о кодировании см. в разделе Кодирование сигнала). Большинство кодов основано на системах счисления, причем использующих позиционный принцип образования числа, при котором значение каждой цифры зависит от ее положения в числе.

Примером позиционной формы записи чисел является та, которой мы пользуемся (так называемая арабская форма чисел). Так, в числах 123 и 321 значения цифры 3, например, определяются ее положением в числе: в первом случае она обозначает три единицы (т.е. просто три), а во втором – три сотни (т.е. триста).

Тогда полное число получается по формуле:

где l – количество разрядов числа, уменьшенное на 1,

i – порядок разряда,

m – основание системы счисления,

a_i – множитель, принимающий любые целочисленные значения от 0 до m -1, и соответствующий цифре i -го порядка числа.

Например, для десятичного (m = 10) числа 345 его полное значение рассчитывается по формуле:

3*10² + 4*10¹ + 5*10⁰ = 345.

Римские числа являются примером полупозиционной системы образования числа: так, в числах IX и XI знак I обозначает в обоих случаях единицу (признак непозиционной системы), но, будучи расположенным слева от знака X (обозначающего десять), вычитается из десяти, а при расположении справа – прибавляется к десяти. В первом случае полное значение числа равно 9, во втором – 11.

 

В современной информатике используются в основном три системы счисления (все – позиционные): двоичная, шестнадцатеричная и десятичная.

 

Двоичная система счисления используется для кодирования дискретного сигнала, потребителем которого является вычислительная техника. Такое положение дел сложилось исторически, поскольку двоичный сигнал проще представлять на аппаратном уровне. В этой системе счисления для представления числа применяются два знака – 0 и 1.

 

Шестнадцатеричная система счисления используется для кодирования дискретного сигнала, потребителем которого является хорошо подготовленный пользователь – специалист в области информатики. В такой форме представляется содержимое любого файла, затребованное через интегрированные оболочки операционной системы, например, средствами Norton Commander в случае MS DOS. Используемые знаки для представления числа – десятичные цифры от 0 до 9 и буквы латинского алфавита – A, B, C, D, E, F.

 

Десятичная система счисления используется для кодирования дискретного сигнала, потребителем которого является так называемый конечный пользователь – неспециалист в области информатики (очевидно, что и любой человек может выступать в роли такого потребителя). Используемые знаки для представления числа – цифры от 0 до 9.

 

Соответствие между первыми несколькими натуральными числами всех трех систем счисления представлено в таблице перевода:

Десятичная система	Двоичная система	Шестнадцатеричная система
		A
		B
		C
		D
		E
		F

 

Для различения систем счисления, в которых представлены числа, в обозначение двоичных и шестнадцатеричных чисел вводят дополнительные реквизиты:

· для двоичных чисел – нижний индекс справа от числа в виде цифры 2 или букв В либо b (binary – двоичный), либо знак B или b справа от числа. Например, 101000₂ = 101000_b = 101000_B = 101000B = 101000b;

· для шестнадцатеричных чисел - нижний индекс справа от числа в виде числа 16 или букв H либо h (hexadecimal – шестнадцатеричный), либо знак H или h справа от числа. Например, 3AB₁₆ = 3AB_H= 3AB_h = 3ABH = 3ABh.

 

Для перевода чисел из одной системы счисления в другую существуют определенные правила. Они различаются в зависимости от формата числа – целое или правильная дробь. Для вещественных чисел используется комбинация правил перевода для целого числа и правильной дроби.