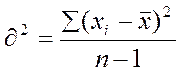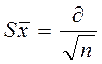На какие две группы разделяются статистические характеристики ряда результатов измерений. Какие характеристики входят в каждую группу.

Представительность выборки?

Представительность — соответствие характеристик выборки характеристикам популяции или генеральной совокупности в целом. Представительность определяет, насколько возможно обобщать результаты исследования с привлечением определённой выборки на всю генеральную совокупность, из которой она была собрана.

Также представительность можно определить как свойство выборочной совокупности представлять параметры генеральной совокупности, значимые с точки зрения задач исследования.

 

На какие две группы разделяются статистические характеристики ряда результатов измерений? Какие характеристики входят в каждую группу?

1-ая группа: «оценка центральной тенденции выборки» (характеристики этой группы позволяют оценить тенденцию выборки) В эту группы входят такие характеристика как: среднее арифметическое значение, медиана, мода.

 

2-ая группа: «характеристика вариации (колеблемости)». В эту группу входят такие характеристики как: размах варьирования, дисперсия, среднее квадратическое отклонение, стандартная ошибка среднего, коэффициент вариации

Что характеризует и как рассчитывается среднее арифметическое значение? Дайте определение моде и медиане.

Среднее арифметическое значение определяется как среднее взвешенное наблюдаемых значений, когда каждое значение характеризуется с учетом частоты его появлений.

Среднее арифметическое определяется по формуле:

где: х – среднее арифметическое, х(i) – сумма всех значений х, n – количество выборки.

Мода – значение числового ряда, которое встречается наиболее часто.

Медиана – середина ранжированного ряда (ряда чисел, расставленных по возрастанию или убыванию).

 

Что характеризуют, как рассчитываются и для чего используются дисперсия и среднее квадратическое отклонение?

Дисперсия — мера разброса случайной величины, то есть её отклонения от математического ожидания (средний квадрат отклонений). Дисперсия отражает меру разброса данных вокруг средней величины.

Дисперсия рассчитывается по формуле:

где: σ – дисперсия, х (i) – x (сред.) – сумма полученная после вычислений в таблице; n-1 – число выборки минус 1.

Средним квадратичным отклонением статистического распределения называется квадратный корень из его дисперсии. Стандартное отклонение, также характеризует меру рассеяния данных, но (в отличие от дисперсии) его можно сравнивать с исходными данными, так как единицы измерения у них одинаковые.

Рассчитывается по формуле:

где: так же как в п.5

Что характеризует, как рассчитывается и для чего служит стандартная ошибка средней арифметической?

Стандартная ошибка средней арифметической отражает диапазон значений, в котором должно находиться среднее значение при использовании других выборочных данных.

Рассчитывается по формуле:

где: Sx (сред) – стандартная ошибка средней арифметической, σ – дисперсия, корень из n – корень из числа выборки.

Что характеризует, как рассчитывается и в каких случаях используется коэффициент вариации?

Коэффициент вариации – наиболее универсальный показатель, отражающий степень разбросанности значений независимо от их масштаба и единиц измерения. Коэффициент вариации измеряется в процентах и может быть использован для сравнения вариации различных процессов и явлений.

Имея коэффициенты вариации, можно сравнивать однородность самых разных явлений независимо от их масштаба и единиц измерения. Данный факт и делает коэффициент вариации столь популярным.

Рассчитывается по формуле:

где: V – коэффициент вариации, σ – дисперсия, х(сред) – среднее значение х.

Расчет основных статистических характеристик ряда результатов измерений.

Составьте расчетную таблицу (см. образец расчета основных статистических характеристик, п.4) и рассчитайте значения основных статистических характеристик для первой из двух выборок, полученных на кафедре биомеханики (выборка Х).

 

 

ТАБЛИЦА СОСТАВЛЯЕТСЯ ПО ВАШЕМУ ВАРИАНТУ КОНТРОЛЬНОЙ РАБОТЫ.

 

Представительность выборки?

Представительность — соответствие характеристик выборки характеристикам популяции или генеральной совокупности в целом. Представительность определяет, насколько возможно обобщать результаты исследования с привлечением определённой выборки на всю генеральную совокупность, из которой она была собрана.

Также представительность можно определить как свойство выборочной совокупности представлять параметры генеральной совокупности, значимые с точки зрения задач исследования.

 

На какие две группы разделяются статистические характеристики ряда результатов измерений? Какие характеристики входят в каждую группу?

1-ая группа: «оценка центральной тенденции выборки» (характеристики этой группы позволяют оценить тенденцию выборки) В эту группы входят такие характеристика как: среднее арифметическое значение, медиана, мода.

 

2-ая группа: «характеристика вариации (колеблемости)». В эту группу входят такие характеристики как: размах варьирования, дисперсия, среднее квадратическое отклонение, стандартная ошибка среднего, коэффициент вариации