
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розкладення періодичних функцій в ряд Фур’є (теорія)Содержание книги
Поиск на нашем сайте У багатьох розділах фізики досліджують коливні періодичні процеси, що описані функцією Перетворення Фур’є здійснює перехід від Ряд Фур’є дає змогу представити періодичний процес
де Для визначення коефіцієнтів використаємо математичні перетворення і отримаємо:
k =1,2,3… Ряд Фур’є можна записати по-іншому:
Набори величин Примітки.1) Якщо значення періоду 2)Для парних функцій ряд містить тільки косинусні гармоніки, для немарних – тільки синусні. 34. Опишіть методику програмування та складові частини проекту “Ряд Фур’є” Оскільки у проекті потрібно обчислювати інтеграли, скористаємось методом правих прямокутників. Позначимо через Тоді в масив
Частинна сума
Для оптимізації обчислень в алгоритмі введено змінну КОМ дійсного типу, у якій при обчисленні Результатом роботи алгоритму є обчислення та виведення на дисплей коефіцієнтів Алгоритм виконання лаб. роботи: 1. Отримати і запрограмувати досліджувану ф-ію як Pascal- функцію. 2. Запрограмувати Pascal- процедуру обчислення ряду Фур’є, вхідними параметрами є масиви 3. Для різних значень 4. Пояснити отримані результати. 5. Побудувати графік залежності Виключні ситуації та їхня обробка в Delphi. Виключення – це ситуація в програмі, яка вимагає спеціальної обробки. Наприклад ділення на 0. При виникнення такої ситуації в Delphi створює екземпляр деякого класу залежно від характеру помилки, що відбулась. Всі такі класи є спадкоємцями класу Exception, який визначено в модулі SysUtiles, що дозволяє Delphi їх розпізнавати. Механізм обробки виключень полягав в достроковому перериванні підпрограми або методу об’єкту в якому відбулась помилка, пошук обробника цього виключення. Якщо обробника не знайдено, то управління передається підпрограмі, що викликала підпрограму з винятковою ситуацією. В Delphi визначено декілька ключових слів, які використовуються у фрагментах програми для обробки виключних ситуацій: try… except, raise, try… finally, at, on-do-else. Блок обробки try… except намагається виконати заданий фрагмент програми, а у разі появи виключення – передає управління спец. обробни-кові, розташованому в секції except. Try <фрагмент програми> Except On <клас виключення> do <обробник виключення> Else <Обробник за умови>; end; Потенційно небезпечний фрагмент програми який може викликати переривання ставиться між ключовими словами try… except, якщо цей фрагмент виконався безпомилково, то решта конструкції задіяна не буде. Якщо в цьому фрагменті виникла виняткова ситуація, то система аналізує якого класу ця ситуація є. Якщо жоден з класів не підходить тоді виконується секція else. Якщо розділ else не використано і при цьому не знайдено обробник виключення, то виключення передається у підпрограму, що викликала дану і так далі відповідно до механізму. Блок обробки Try…Except використовують у ситуаціях коли відомо, як саме потрібно реагувати на помилку, що відбулась, навіть якщо програма не намагалась встановити її тип. Для генерування власного виключення використовують ключове слово raise. Raise <екземпляр класу виключення>; Коли реакція програми на помилку не так важлива, як коректне завершення фрагмента програми, що викликав цю помилку. Такі ситуації зазвичай пов’язані з необхідністю повертати ОС ресурси, виділені помилковому фрагменту програми. При чому повернення ресурсів повинне відбутися як у разі успішного так і у разі помилкового виконання фрагмента програми. Для реалізації такої поведінки програми використовують блок обробки try… finally. Try <фрагмент програми1> Finally < фрагмент програми2> end;
|
||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 276; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.009 с.) |

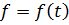 , яка визначена для всіх дійсних значень аргументу t і має властивість
, яка визначена для всіх дійсних значень аргументу t і має властивість  ,де
,де 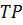 – період коливань.
– період коливань.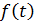 до функції іншого аргументу
до функції іншого аргументу  , де
, де 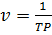 . Якщо аргументом є час, то
. Якщо аргументом є час, то 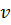 – лінійна частота. Перехід
– лінійна частота. Перехід  називають прямим перетворенням Фур’є, а
називають прямим перетворенням Фур’є, а 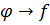 – зворотним перетворенням. Якщо функцію задано у формі таблиці, наприклад, отримано з експерименту, то використовують дискретне перетворення Фур’є.
– зворотним перетворенням. Якщо функцію задано у формі таблиці, наприклад, отримано з експерименту, то використовують дискретне перетворення Фур’є.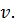
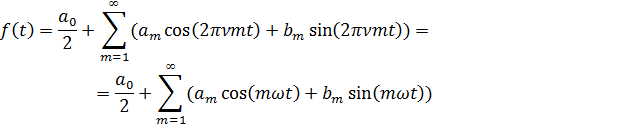
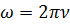 - кругова частота
- кругова частота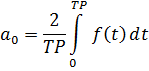
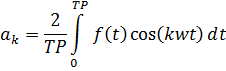
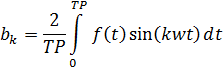
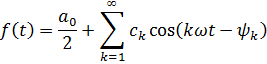
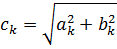

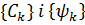 залежать від
залежать від 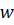 . Їх називають відповідно, амплітудним і фазовим спектром функції
. Їх називають відповідно, амплітудним і фазовим спектром функції 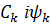 від
від 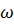 є дискретними.
є дискретними.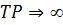 дискреткретний спектр стає неперервним і ряд Фур’є переходить у інтеграл Фур’є.
дискреткретний спектр стає неперервним і ряд Фур’є переходить у інтеграл Фур’є.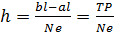 крок дискретизації ф-ії на періоді TP. Дискретизацію виконаємо шляхом табулювання заданої функції, ввівши проміжок al..bl, точніть Eps та кількість точок графіку Ne.
крок дискретизації ф-ії на періоді TP. Дискретизацію виконаємо шляхом табулювання заданої функції, ввівши проміжок al..bl, точніть Eps та кількість точок графіку Ne.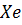 будуть записані значення аргументу
будуть записані значення аргументу 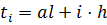 , а в масив
, а в масив 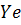 - дискретні значення функції
- дискретні значення функції  . Згідно методу правих прямокутників:
. Згідно методу правих прямокутників: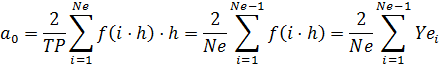
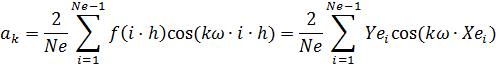
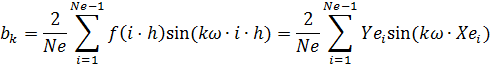
 членів ряду (гармонік) набуде вигляду:
членів ряду (гармонік) набуде вигляду: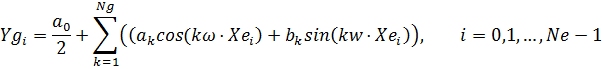
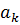 та
та 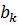 поза цикл винесено значення КОМ=
поза цикл винесено значення КОМ= 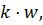 а при обчисленні
а при обчисленні 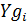 змінній КОМ присвоюється
змінній КОМ присвоюється 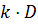 , де
, де 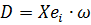 .
.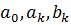 , амплітудного спектра
, амплітудного спектра 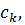 і формування
і формування 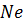 значень масиву
значень масиву  , які обчислено відповідно до ф-ли
, які обчислено відповідно до ф-ли  =… для точок
=… для точок 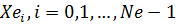 .
.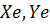 і число
і число 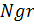 з діапазону [100..600] побудувати графіки залежностей
з діапазону [100..600] побудувати графіки залежностей 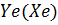 та
та  .
.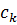 від
від 


