Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимизация структуры и устойчивость движения двухдвигательного асинхронного электропривода с системой ПЧ-АДСодержание книги
Поиск на нашем сайте
Как указывалось выше, двухдвигательный асинхронный электропривод с системой ПЧ-АД (см. рисунок 2.5) состоит из двух асинхронных двигателей, работающих на один вал. Известно, что при работе двух двигателей на один вал нагрузка будет распределена поровну только в том случае, когда их механические характеристики совпадают. Практически достичь этого невозможно [9]. Это объясняется тем, что согласно действующему ГОСТу допуск на скольжение при изготовлении асинхронных двигателей составляет +25%. Поэтому двигатели одного и того же типоразмера могут иметь различные скольжения при номинальной нагрузке на валу. Если номинальные моменты двух идентичных двигателей обозначить через Мн, а их фактические скольжения соответствующие этому моменту S1 и S2, то при работе этих двигателей на один вал они будут развивать моменты, равные
где S общее скольжение, с которым будут работать двигатели. Учитывая, что суммарный момент, развиваемый двигателем при нормальной их загрузке, равен
откуда
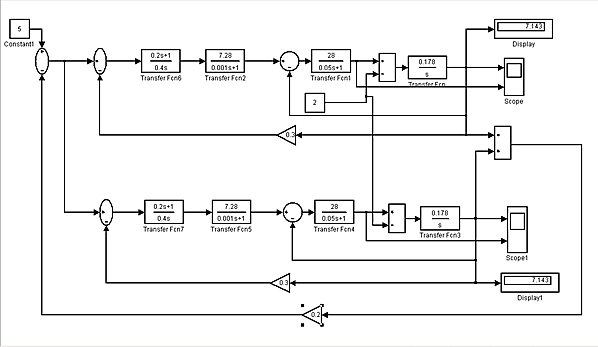
Таким образом, распределение суммарной нагрузки между двумя двигателями, работающими на один вал, имеют идентичные характеристики, а напряжения, подводимые на зажимы двигателей, одинаковы. Поэтому данное условие учитывается в дальнейшем при оптимизации структурной схемы модели двухдвигательного асинхронного электропривода (ДАЭП с ПЧ-АД). Предполагаемая структурная схема модели ДАЭП с ПЧ-АД представлена на рисунке 2.6.
Рисунок 2.6 - Структурная схема модели двухдвигательного асинхронного электропривода (ДАЭП с ПЧ-АД)
Для сравнения предложенной структурной схемы модели ДАЭП с ПЧ-АД с другими оптимизированными структурами, рассмотрим устойчивость движения ДАЭП с ПЧ-АД и переходной процесс суммирующего сигнала скоростей двигателей этого двухдвигательного асинхронного электропривода. Устойчивость движения ДАЭП с ПЧ-АД будем рассматривать на основании характеристического уравнения передаточной функции ДАЭП. Для получения передаточной функции ДАЭП составляется программа в системе MATLAB. Полученная программа в системе MATLAB представлена на рисунке 2.7.
>> n=[0.178]; >> m=[1 0]; >> W1=tf(n,m)
Transfer function: (передаточная функция)
0.178 ----- s
>> n2=[28]; >> m2=[0.05 1]; >> W2=tf(n2,m2)
Transfer function: (передаточная функция) ---------- 0.05 s + 1
>> G1=W1*W2
Transfer function: (передаточная функция) 4.984 ------------ 0.05 s^2 + s
>> Q1=feedback(G1,[1])
Transfer function: (передаточная функция) 4.984 -------------------- 0.05 s^2 + s + 4.984
>> n3=[7.28]; >> m3=[0.001 1]; >> W3=tf(n3,m3)
Transfer function: (передаточная функция) 7.28 ----------- 0.01 s + 1
>> n4=[0.15 1]; >> m4=[0.4 0]; >> W4=tf(n4,m4)
Transfer function: (передаточная функция) 0.15 s + 1 ---------- 0.4 s
>> C1=Q1*W3*W4
Transfer function: (передаточная функция разомкнутой системы ПЧ - АД)
5.443 s + 36.28 --------------------------------------------- 2e-005 s^4 + 0.0204 s^3 + 0.402 s^2 + 1.994 s
>> Wc1=feedback(C1,[0.3])
Transfer function: (передаточная функция замкнутой системы ПЧ - АД) 5.443 s + 36.28 ----------------------------------------------------- 2e-005 s^4 + 0.0204 s^3 + 0.402 s^2 + 3.626 s + 10.89
>> Wc2=Wc1
Transfer function: 5.443 s + 36.28 ----------------------------------------------------- 2e-005 s^4 + 0.0204 s^3 + 0.402 s^2 + 3.626 s + 10.89
>> Dv=parallel(Wc1,Wc2)
Transfer function: (передаточная функция разомкнутого двухдвигательного электропривода) 0.0002177 s^5 + 0.2235 s^4 + 5.856 s^3 + 68.64 s^2 + 381.6 s + 789.9 ---------------------------------------------------------------- 4e-010 s^8 + 8.16e-007 s^7 + 0.0004322 s^6 + 0.01655 s^5 + 0.31 s^4 + 3.36 s^3 + 21.9 s^2 + 78.95 s + 118.5
>> h1=[0.2]; >> z1=[1]; >> Woc=tf(h1,z1)
Transfer function: 0.2
>> Wc=feedback(Dv,Woc,-1)
Transfer function: (передаточная функция замкнутого двухдвигательного электропривода) 0.0002177 s^5 + 0.2235 s^4 + 5.856 s^3 + 68.64 s^2 + 381.6 s + 789.9 --------------------------------------------------------------- 4e-010 s^8 + 8.16e-007 s^7 + 0.0004322 s^6 + 0.01659 s^5 + 0.3547 s^4 + 4.531 s^3 + 35.63 s^2 + 155.3 s + 276.5
>> P = [4e-10 8.16e-7 0.0004322 0.01659 0.3547 4.531 35.63 155.3 276.5]; (характеристическое уравнение) >> r = roots(P)
Корни характеристического уравнения: r = 1.0e+003 * -1.0103 -0.9900 -0.0068 + 0.0126i -0.0068 - 0.0126i -0.0073 + 0.0071i -0.0073 - 0.0071i -0.0063 -0.0052 Рисунок 2.7 - Программа определения устойчивости ДАЭП с системой ПЧ-АД
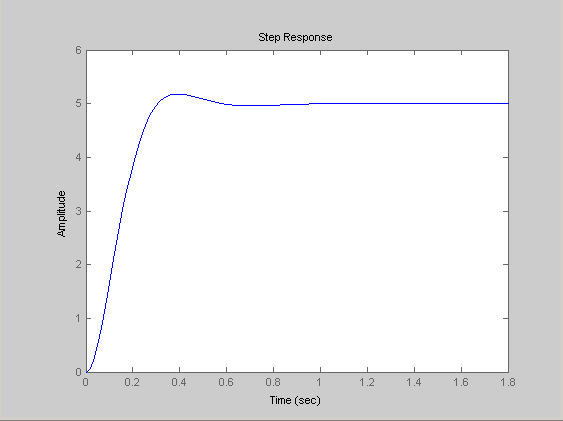
Из представленной программы (см. рисунок 2.7) видно, что движение ДАЭП с системой ПЧ-АД устойчивое, так как корни характеристического уравнения (r) с отрицательной вещественной частью. Переходной процесс суммирующего сигнала S∑ показан на рисунке 2.8.
Рисунок 2.8 - Переходной процесс суммирующего сигнала S∑ ДАЭП с ПЧ-АД
Однако, структурная схема модели ДАЭП с ПЧ-АД с обратной связью по скорости (см. рисунок 2.6) может быть представлена без обратных связей по скорости системы ПЧ-АД (см. рисунок 2.9).
Рисунок 2.9 - Структурная схема модели ДАЭП с ПЧ-АД без обратных связей по скорости
Это связано с тем, что предложенная обратная связь суммирующего сигнала скоростей двигателей подается на вход ДАЭП, обеспечивая при этом соответствующую устойчивость движения ДАЭП с ПЧ-АД без обратных связей по скорости. Устойчивость такой системы рассмотрим так же по корням характеристического уравнения данной модели. Программа определения устойчивости движения дается на рисунке 2.10.
>> n=[0.178]; >> m=[1 0]; >> W1=tf(n,m)
Transfer function:(передаточная функция) 0.178 ----- s
>> n2=[28]; >> m2=[0.05 1]; >> W2=tf(n2,m2)
Transfer function: (передаточная функция) ---------- 0.05 s + 1
>> G1=W1*W2
Transfer function: 4.984 ------------ 0.05 s^2 + s
>> Q1=feedback(G1,[1])
Transfer function: (передаточная функция) 4.984 -------------------- 0.05 s^2 + s + 4.984
>> n3=[7.28]; >> m3=[0.001 1]; >> W3=tf(n3,m3)
Transfer function: (передаточная функция) 7.28 ----------- 0.001 s + 1
>> n4=[0.15 1]; >> m4=[0.4 0]; >> W4=tf(n4,m4)
Transfer function: 0.15 s + 1 ---------- 0.4 s
>> C1=Q1*W3*W4
Transfer function: (передаточная функция системы ПЧ-АД без обратной связи по скорости) 5.443 s + 36.28 --------------------------------------------- 2e-005 s^4 + 0.0204 s^3 + 0.402 s^2 + 1.994 s
>> Wc1=C1
Transfer function: 5.443 s + 36.28 --------------------------------------------- 2e-005 s^4 + 0.0204 s^3 + 0.402 s^2 + 1.994 s
>> Wc2=C1
Transfer function: (передаточная функция)
5.443 s + 36.28 --------------------------------------------- 2e-005 s^4 + 0.0204 s^3 + 0.402 s^2 + 1.994 s
>> Wc=parallel(Wc1,Wc2)
Transfer function: (передаточная функция ДАЭП) 0.0002177 s^5 + 0.2235 s^4 + 5.856 s^3 + 50.87 s^2 + 144.7 s ------------------------------------------------------------------------ 4e-010 s^8 + 8.16e-007 s^7 + 0.0004322 s^6 + 0.01648 s^5 + 0.2429 s^4 + 1.603 s^3 + 3.974 s^2
>> h1=[0.2]; >> z1=[1]; >> Woc=tf(h1,z1)
Transfer function: (передаточная функция) 0.2
>> Wd=feedback(Wc,Woc,-1)
Transfer function: (передаточная функция ДАЭП с обратной связью по суммирующему сигналу скоростей) 0.0002177 s^5 + 0.2235 s^4 + 5.856 s^3 + 50.87 s^2 + 144.7 s ------------------------------------------------------------------------- 4e-010 s^8 + 8.16e-007 s^7 + 0.0004322 s^6 + 0.01652 s^5 + 0.2876 s^4 + 2.774 s^3 + 14.15 s^2 + 28.93 s
>> P = [4e-10 8.16e-7 0.0004322 0.01652 0.2876 2.774 14.15 28.93];
>> r = roots(P) (корни характеристического уравнения) r = 1.0e+003 * -1.0096 -0.9905 -0.0071 + 0.0088i -0.0071 - 0.0088i -0.0104 -0.0096 -0.0057 Рисунок 2.10 - Программа определения устойчивости движения ДАЭП с ПЧ-АД без обратных связей по скорости Из представленной программы (см. рисунок 2.10) видно, что движение ДАЭП с ПЧ-АД без обратных связей по скорости устойчивое, так как корни характеристического уравнения (r) с отрицательной вещественной частью. Переходной процесс суммирующего сигнала S∑ показан на рисунке 2.11.
Рисунок 2.11 - Переходной процесс суммирующего сигнала S∑ ДАЭП с ПЧ-АД без обратных связей по скорости Но указанную выше структуру ДАЭП с ПЧ-АД без обратных связей по скорости (см. рисунок 2.9) можно так же оптимизировать по количеству элементов, т.е. где будет использован один преобразователь частоты и одно корректирующее устройство, с целью обеспечения экономии затрат электроэнергии и надежности работы этого ДАЭП. Структурная схема ДАЭП с системой ПЧ-АД без обратных связей по скорости с одним преобразователем частоты и одним корректирующим устройством представлена на рисунке 2.12.
Рисунок 2.12 - Структурная схема ДАЭП с системой ПЧ-АД без обратных связей по скорости с одним преобразователем частоты и одним корректирующим устройством
Программа определения устойчивости движения дается на рисунке 2.13.
>> n=[0.178]; >> m=[1 0]; >> W1=tf(n,m)
Transfer function: 0.178 ----- s
>> n2=[28]; >> m2=[0.05 1]; >> W2=tf(n2,m2)
Transfer function: ---------- 0.05 s + 1
>> G1=W1*W2
Transfer function: 4.984 ------------ 0.05 s^2 + s
>> Q1=feedback(G1,[1])
Transfer function: 4.984 -------------------- 0.05 s^2 + s + 4.984
>> Q2=Q1
Transfer function: 4.984 -------------------- 0.05 s^2 + s + 4.984
>> Wob=parallel(Q1,Q2)
Transfer function: 0.4984 s^2 + 9.968 s + 49.68 -------------------------------------------------- 0.0025 s^4 + 0.1 s^3 + 1.498 s^2 + 9.968 s + 24.84
>> n3=[7.28]; >> m3=[0.001 1]; >> W3=tf(n3,m3)
Transfer function: 7.28 ----------- 0.001 s + 1
>> n4=[0.15 1]; >> m4=[0.4 0]; >> W4=tf(n4,m4)
Transfer function: 0.15 s + 1 ---------- 0.4 s
>> G1=Wob*W3*W4
Transfer function: 0.5443 s^3 + 14.51 s^2 + 126.8 s + 361.7 ------------------------------------------------------------------------ 1e-006 s^6 + 0.00104 s^5 + 0.0406 s^4 + 0.6033 s^3 + 3.997 s^2 + 9.936 s
>> h1=[0.2]; >> z1=[1]; >> Woc=tf(h1,z1)
Transfer function: 0.2
>> Ws=feedback(G1,Woc,-1)
Transfer function: 0.5443 s^3 + 14.51 s^2 + 126.8 s + 361.7 ------------------------------------------------------------------------ 1e-006 s^6 + 0.00104 s^5 + 0.0406 s^4 + 0.7122 s^3 + 6.9 s^2 + 35.3 s +72.33
>> P = [1e-6 0.00104 0.0406 0.7122 6.9 35.3 72.33]; >> r = roots(P) r = 1.0e+003 * -1.0001 -0.0071 + 0.0087i -0.0071 - 0.0087i -0.0106 -0.0094 -0.0057 Рисунок 2.13 - Программа определения устойчивости движения ДАЭП с системой ПЧ-АД без обратной связи по скорости с одним регулятором скорости и с одним преобразователем частоты
Из представленной программы (см. рисунок 2.13) видно, что движение ДАЭП с системой ПЧ-АД без обратных связей по скорости с одним регулятором скорости и с одним преобразователем частоты устойчивое, так как корни характеристического уравнения (r) с отрицательной вещественной частью. Переходной процесс суммирующего сигнала S∑ показан на рисунке 2.14.
Рисунок 2.14 - Переходной процесс суммирующего сигнала S∑ ДАЭП с ПЧ-АД без обратных связей по скорости
|
|||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 1035; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.35.234 (0.01 с.) |

 , (2.22)
, (2.22) , (2.23)
, (2.23)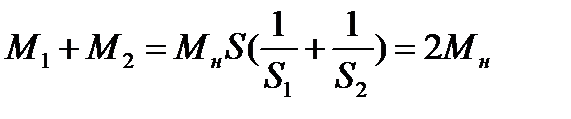 , (2.24)
, (2.24) . (2.25)
. (2.25)