
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принятие решений в условиях неопределенности. Критерии Сэвиджа и Лапласа. ⇐ ПредыдущаяСтр 3 из 3
Критерий Сэвиджа (минимаксный). Суть его заключается в выборе стратегии, не допускающей слишком высоких потерь. Для этого используется матрица рисков, в которой вычисляется максимальная прибыль при каждом варианте действия игрока, и среди результатов выбирается наименьший. Его формула выглядит как min (max i)
Если принимающий решение является игроком B, то критерий становится таким: Неопределенность типа «активный партнер». Гипотезы 1, 2 и 3 о поведении партнера Гипотеза 1. Каждый из субьектов А и Б не имеет информации о выборе, который сделан второй стороной. Дополнительные гипотезы о характере поведения второго игрока отсутствуют. В этом случае можно поступать аналогично решению задачи в условиях полной неопределенности. Это, по-существу, в точности тот же случай, и мы можем воспользоваться известным принципом наилучшего гарантированного результата. Для субьекта А гарантированная оценка будет равна I* = max min I(x,z), xÎX zÎZ а для субьекта Б: I* = max minI(x,z) zÎZ xÎX Решая задачи максимизации, мы находим и векторы x*,z*, реализующие соответствующие гарантированные оценки. Гипотеза 2. Предполагаем, что субъект Б следует принципу максимина и выбирает z* из условия Гипотезы 1: I* = max min I(x,z). zÎZ xÎX Тогда мы можем выбирать x согласно правилу I (x,z*) ®max, xÎX где z* - гарантирующее решение второго игрока. Обозначим решение задачи (18) через x**. При этом оказывается, что I** = I(x**,z*) ³ I*, где I* - наша гарантированная оценка, получаемая по принципу максимина. Гипотеза 3. Мы теперь можем допустить, что субъект рассуждает точно так же, как и мы в предыдущем случае, т.е. использует не стратегию z*, а аналогичную стратегию z**. Поэтому мы можем это учесть и выбирать оптимальное решение с учетом уже этой гипотезы:I(x,z**) ® max Þx***,I***. xÎX Неопределенность типа «активный партнер». Гипотезы о знании первых ходов субъектов А и Б.
Мы по условиям игры знаем первый ход субъекта Б (он нам его обязан сообщить). Тогда наше поведение будет определяться стратегией в виде функции x=x(z). Мы можем ее определить в результате решения задачи оптимизации I(x,z) ®max. Условие позволяет для каждого фиксированного z определить искомое значение x, т.е. задать функцию x(z). Для этого случая мы также можем определить гарантированный результат j1( min I( Так как x’, Принцип устойчивости Нэша. по имени автора - американского математика Джона Нэша. Он гласит, что выбор рациональной стратегии h должен производиться среди множества точек равновесия. Равновесные решения называются так же оптимальными по Нэшу. Данный принцип отражает очень важное свойство коллективного решения. Именно, если оба субъекта А и Б смогли договорится о том, чтобы придерживаться выбора x= Множество Парето. Множество, включающее в себя все эффективные решения, обозначается PI(X) или просто P(X) (если ясно, о каком векторном критерии I идет речь) и называется множеством Парето для векторного отображения I: Х
Смысл введенного понятия эффективного решения состоит в том, что оптимальное решение следует искать только среди элементов множества P(X) (принцип Парето). В противном случае всегда найдется точка x
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 208; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.195.110 (0.02 с.) |
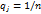 .
.
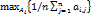
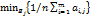
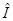 :
: 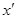 и
и 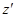 , очевидно, справедливо неравенство
, очевидно, справедливо неравенство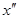 ,
, 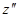 ). Отсюда имеем: j1(
). Отсюда имеем: j1(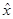 , z=
, z= 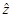 , то тот субъект, который нарушает договоренность, прежде всего и пострадает: свойство устойчивости решения дает известную гарантию против нарушения договоренности. Все вышеизложенное справедливо и для случая N игроков, где N>2.
, то тот субъект, который нарушает договоренность, прежде всего и пострадает: свойство устойчивости решения дает известную гарантию против нарушения договоренности. Все вышеизложенное справедливо и для случая N игроков, где N>2.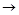 Em, I = (I1,I2...,Im). Очевидно, P(X)
Em, I = (I1,I2...,Im). Очевидно, P(X)  X. Образ множества P(X) в пространстве критериев Em обозначается P(I). Множество P(I) = I(P(X)) называется множеством э ффективных оценок. Множество эффективных оценок часто также называется множеством Парето в пространстве критериев.
X. Образ множества P(X) в пространстве критериев Em обозначается P(I). Множество P(I) = I(P(X)) называется множеством э ффективных оценок. Множество эффективных оценок часто также называется множеством Парето в пространстве критериев. X, оказывающаяся более предпочтительной с учетом всех частных целевых функций Ii(x). Точка
X, оказывающаяся более предпочтительной с учетом всех частных целевых функций Ii(x). Точка  I(S(X)).
I(S(X)).


