
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
І. Еквівалентність лотерейних та матричних моделей прийняття рішенняСодержание книги
Поиск на нашем сайте
І. Еквівалентність лотерейних та матричних моделей прийняття рішення І.1. Непараметрична ситуація прийняття рішення (НСПР) І.1.а. Приклад НСПР
Подруга запросила мене у гості, щоб оцінити її новий домашній кінотеатр. Мені відомо про її захоплення щодо переглядів фільмів, тому я вирішила подарувати їй DVD, але обізнана в її смаках досить погано. Спочатку я виділила за допомогою Інтернету найбільш популярні жанри фільмів серед молоді. Ось який вибір постав переді мною: 1. Фантастика. 2. Комедія. 3. Містика. 4. Драма. Я вирішила звернутися до її брата, щоб він оцінив, яка ймовірність того, що мій подарунок сподобається подрузі, оскільки він більш менш знає її уподобання. Після цього я отримала наступні результати. 1. Фантастика: a. DVD дуже сподобається - 0,9. b. DVD зовсім не сподобається - 0 c. Інколи дивиться даний жанр, але в залежності від настрою - 0,1. 2. Комедія: a. DVD дуже сподобається - 0. b. DVD зовсім не сподобається - 0,6 c. Інколи дивиться даний жанр, але в залежності від настрою - 0,4. 3. Містика: a. DVD дуже сподобається - 0,3. b. DVD зовсім не сподобається - 0,4. c. Інколи дивиться даний жанр, але в залежності від настрою - 0,3.
4. Драма: a. DVD дуже сподобається - 0. b. DVD зовсім не сподобається - 0,5. c. Інколи дивиться даний жанр, але в залежності від настрою - 0,5.
Наступний крок - позначення дій та наслідків.
Множина дій
u1 - подарувати DVD-диск з фантастикою; u2 - подарувати DVD-диск з комедією; u3 - подарувати DVD-диск з містикою; u4 - подарувати DVD-диск з драмою.
Множина дій
c1 - DVD дуже сподобається; c2 - DVD зовсім не сподобається; с3 - Інколи дивиться даний жанр, але в залежності від настрою.
На множині наслідків С існує розподіл ймовірностей Q, які нам дають додаткову інформацію про невизначеність. Суть її полягає у тому, що невідомо, якому саме DVD я надам перевагу.
Маємо наступні розподіли ймовірностей:
Далі сформулюємо таблицю:
Непараметрична ситуація описується через лотерейну схему, що видно з рисунку 1.
Рисунок 1. Лотерейна схема
І.1.в. Перехід від лотерейної моделі до матричної
Для переходу від лотерейної до матричної моделі необхідно визначити множини Θ, U і C, функцію G(θ, u) та розподіл Р на Θ. Множини U і C переносяться без змін, а множину Θ знаходиться наступним чином: Θ = {θ
Знайдемо множину Θ:
Θ = { (c1,c2,c1,c2), (c3,c2,c1,c2), (c1,c3,c1,c2), (c3,c3,c1,c2), (c1,c2,c2,c2), (c3,c2,c2,c2), (c1,c3,c2,c2), (c3,c3,c2,c2), (c1,c2,c3,c2), (c3,c2,c3,c2), (c1,c2,c3,c2), (c3,c3,c3,c2), (c1,c2,c1,c3), (c3,c2,c1,c3), (c1,c3,c1,c3), (c3,c3,c1,c3), (c1,c2,c2,c3), (c3,c2,c2,c3), (c1,c3,c2,c3), (c3,c3,c2,c3), (c1,c2,c3,c3), (c3,c2,c3,c3), (c1,c2,c3,c3), (c3,c3,c3,c3) }.
Маємо наступні вихідні дані функції G(θ, u), для якої G(θ, u) = θ(u), матиме вигляд:
На рисунку 2 представлена матрична схема:
Для перенесення інформації слід побудувати розподіл Р на Θ. Розподіл Р – сумісний розподіл чотирьох випадкових величин Cu1, Cu2, Cu3, Cu4, відповідних наслідків для трьох рішень. Події настання наслідків для кожного з рішень є незалежними, тому ймовірності обчислюються за формулою:
Маємо:
P1(c1,c2,c1,c2)=0,9*0,6*0,3*0,5=0,081 P2(c3,c2,c1,c2)=0,1*0,6*0,3*0,5=0,009 P3(c1,c3,c1,c2)=0,9*0,4*0,3*0,5=0,054 P4(c3,c3,c1,c2)=0,1*0,4*0,3*0,5=0,006 P5(c1,c2,c2,c2)=0,9*0,6*0,4*0,5=0,108 P6(c3,c2,c2,c2)=0,1*0,6*0,4*0,5=0,012 P7(c1,c3,c2,c2)=0,9*0,4*0,4*0,5=0,072 P8(c3,c3,c2,c2)=0,1*0,4*0,4*0,5=0,008 P9(c1,c2,c3,c2)=0,9*0,6*0,3*0,5=0,081 P10(c3,c2,c3,c2)=0,1*0,6*0,3*0,5=0,009 P11(c1,c2,c3,c2)=0,9*0,6*0,3*0,5=0,081 P12(c3,c3,c3,c2)=0,1*0,4*0,3*0,5=0,006 P13(c1,c2,c1,c3)=0,9*0,6*0,3*0,5=0,081 P14(c3,c2,c1,c3)=0,1*0,6*0,3*0,5=0,009 P15(c1,c3,c1,c3)=0,9*0,4*0,3*0,5=0,054 P16(c3,c3,c1,c3)=0,1*0,4*0,3*0,5=0,006 P17(c1,c2,c2,c3)=0,9*0,6*0,4*0,5=0,108 P18(c3,c2,c2,c3)=0,1*0,6*0,4*0,5=0,012 P19(c1,c3,c2,c3)=0,9*0,4*0,4*0,5=0,072 P20(c3,c3,c2,c3)=0,1*0,4*0,4*0,5=0,008 P21(c1,c2,c3,c3)=0,9*0,6*0,3*0,5=0,081 P22(c3,c2,c3,c3)=0,1*0,6*0,3*0,5=0,009 P23 c1,c2,c3,c3)=0,9*0,6*0,3*0,5=0,081 P24(c3,c3,c3,c3)=0,1*0,4*0,3*0,5=0,006
Ми здійснили перехід від лотерейної до матричної схеми без втрат інформації.
І.1.г. Перехід від матричної моделі до лотерейної
Необхідно перетворити матричну модель
в лотерейну, тобто
яка складається з лотерейної схеми
та інформації Треба побудувати відображення
Маємо:
Тепер треба перенести інформацію. При дії
Оскільки ми вважаємо, що є тільки одне істинне значення параметра
Тому
Таким чином
Аналогічно виконуємо наступні розрахунки:
Дискретні розподіли:
Оскільки операція проектування матричної моделі в лотерейну є однозначною, ми отримали вихідну лотерейну модель нашої задачі прийняття рішень.
І.1.а. Приклад ПСПР
Всі знають, що у грудні 2012 року пророкують кінець світу. Але в мене багато планів на життя, тому ці пророкування мені зовсім не підходять. Але життя, таке непередбачене, що завжди треба бути напоготові. Обдумавши, я виокремила декілька варіантів моїх можливих дій. Я можу продати всю свою власність, кинути навчання й робити по життю тільки те, що приносить мені насолоду, тобто подорожувати по всій Європі, відвідуючи різноманітні BEST events та моїх друзів. Або продовжити отримувати освіту, part-time job у вільний час для можливості відкладати гроші на термінові потреби, при цьому тільки інколи подорожувати. Це можливі дії у випадку не настання кінця світу. Третій варіант – все-таки продовжити навчання, оскільки без вищої освіти зараз "нікуди", постійно знаходитися в Києві, витрачати гроші на все, що заманеться.
Наступний крок - позначення дій, наслідків та параметрів.
Дії: u1 – продати власність, кинути навчання і подорожувати по всій Європі u2 – навчатися, part-time job, відкладати гроші на термінові потреби u3 – продовжити навчання, витрачати гроші на все, що заманеться
Параметри: θ1 – кінець світу настане у грудні 2012 року θ 2 – кінець світу омине нас θ 3 – виживуть тільки деякі, у тому числі й я.
Наслідки: c1 – мій вибір правильний на всі 100, життя - вдалося; c2 – у мене депресія, життя немає більше сенсу; с3 – все склалося непогано, але могло бути ліпше; c4 – я розумію, що пішла невірним шляхом, відчуваю себе погано.
Схема:
Введемо розподіл на P на Θ. Відповідно до світових досліджень:
· ймовірність того, що настане кінець світу P( · кінець світу омине нас P( · виживуть тільки деякі, у тому числі й я P(
І. Еквівалентність лотерейних та матричних моделей прийняття рішення
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 160; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.98.39 (0.007 с.) |

 , елементами якої є:
, елементами якої є: , елементами якої є:
, елементами якої є: кожній дії ставиться у відповідність набір наслідків.
кожній дії ставиться у відповідність набір наслідків. - схема непараметричної ситуації.
- схема непараметричної ситуації. модель непараметричної ситуації. IЛ – дані про ситуацію.
модель непараметричної ситуації. IЛ – дані про ситуацію.






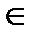 (U → C):
(U → C):  θ(u)
θ(u)  }.
}.
 Θ
Θ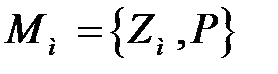



 .
. , яке буде задовольняти умові
, яке буде задовольняти умові




 наслідок
наслідок  наступає при будь-якому значенні параметра
наступає при будь-якому значенні параметра  , для якого
, для якого  . Тому розумно встановити між розподілами
. Тому розумно встановити між розподілами  і
і  таку залежність
таку залежність
 , то події
, то події  є несумісними, а отже для будь якої їх суми справедливо
є несумісними, а отже для будь якої їх суми справедливо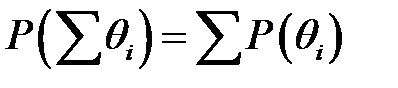

 0,9
0,9
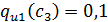

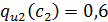
 0,4
0,4



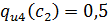

 ) = 0,1;
) = 0,1;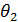 )= 0,7;
)= 0,7; ) = 0,2.
) = 0,2.



