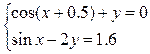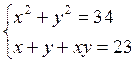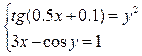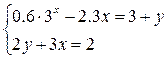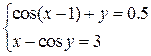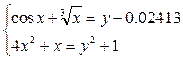Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приближённым способом с заданной точностьюСодержание книги Поиск на нашем сайте
G Напоминание из курса математики: 1. F2 (x,y) = 0 с неизвестными x и y называется множество значений неизвестных, обращающих одновременно оба уравнения системы в тождества. 2. Графическим решением системы 2-х нелинейных уравнений являются координаты (x,y) точки пересечения графиков функций: y = f1(x) и y = f2(x) 3. Приближённое решение системы 2-х уравнений состоит из трёх этапов: - определение отрезка оси Ох из области определения функций f1(x) и f2(x), в котором могут быть решения системы; - нахождение грубо приближённых значений решения системы; - уточнение найденных грубых приближений до заданной точности. Алгоритм решения системы 2-х нелинейных уравнений приближённым (таблично- графическим) способом с заданной точностью ε: 1) Отделить решение – установить отрезок [a;b] оси Ох, в котором могут быть решения данной системы. 2) Протабулировать функции y=f1(x) и y=f2(x) в этом отрезке (см. рис.17). 3) Построить графики функций по полученным табличным значениям. 4)
5) 5.4.1. Задание. Решить систему уравнений
таблично-графическим способом с точностью e=0,0001. Выполнить проверку с помощью подбора параметра. Методические указания к выполнению задания 1. 2. 3. Для всех значений аргумента х вычислить. 4. Построить графики функций по полученным табличным значениям.
5. - задать значения а=0,6, b=0,7 (в концах этого отрезка разность принимает значения разных знаков); - - наименьшая разность = -0,03; - - в этом отрезке достигается необходимая точность: = 0,0001 - решение системы в отрезке [0,65;0,66]: х=0,65330, у=-2,6660 получено за два шага уточнений (итераций). 6. - - вычислить y как y =f1(x) или y =f2(x). 5.4.2. Варианты заданий по теме: «Решение системы 2-х нелинейных уравнений» Решить систему нелинейных уравнений с заданной точностью e = 0,001. Выполнить проверку с помощью итераций.
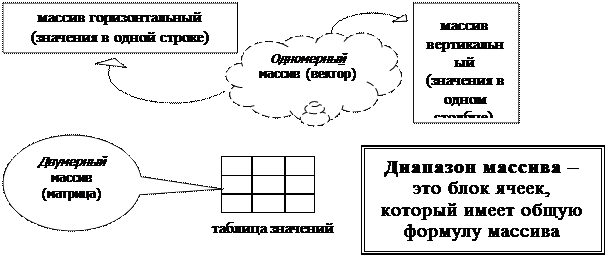
6. Лабораторная работа по теме: «Массивы» Цель работы: изучение матричных операций и операций с векторами в Excel, реализуемых с помощью формул массива. Теоретическая справка. Формулы массива называют также табличными формулами. Формулы массива — очень мощное средство Excel, позволяющее в формулах обращаться с блоком ячеек, как с единым целым. Такие формулы позволяют давать компактные решения сложных задач. Массивы можно использовать для создания формул, которые возвращают некоторое множество результатов или оперируют множеством значений, а не отдельными значениями. Формула массива использует несколько множеств значений, называемых массивами аргументов, и возвращает одно или несколько значений.
Правила применения формулы массива: 1) выделить ячейку или диапазон, который будет содержать результаты (диапазон такого же размера и формы, что и диапазон с исходными данными); 2) ввести формулу вычисления выражения, содержащего массивы аргументов;
3) нажать Ctrl + Shift + Enter для фиксации ввода формулы массива Excel заключает формулу в фигурные скобки (признак формулы массива). G Примечания. 1. Редактировать отдельные ячейки массива нельзя. Ячейки в диапазоне массива рассматриваются как единое целое, и редактировать их надо все сразу. 2. Для изменения или очистки массива следует выделить весь массив и активизировать строку формул. (Фигурные скобки вокруг формулы исчезнут.) Изменить или очистить формулу и нажать Ctrl + Shift + Enter.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 288; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.113.79 (0.01 с.) |

 Решением системы 2-х нелинейных уравнений вида: F1(x,y) = 0
Решением системы 2-х нелинейных уравнений вида: F1(x,y) = 0 Вычислить f1(x) - f2(x) на выбранном отрезке.
Вычислить f1(x) - f2(x) на выбранном отрезке.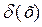
 Пример выполнения задания:
Пример выполнения задания: Определить приближенные значения отрезка Ох, в котором может быть решение данной системы. Возьмем отрезок [0;1]. (Отрезок выбирать исходя из области допустимых значений х).
Определить приближенные значения отрезка Ох, в котором может быть решение данной системы. Возьмем отрезок [0;1]. (Отрезок выбирать исходя из области допустимых значений х).
 Протабулировать функции и в этом отрезке (см. рис.17).
Протабулировать функции и в этом отрезке (см. рис.17). Рис.17. Решение системы 2-х нелинейных уравнений (пример 5.4.1.)
Рис.17. Решение системы 2-х нелинейных уравнений (пример 5.4.1.)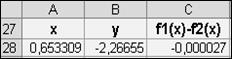 подобрать =0 для х;
подобрать =0 для х;