
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Как распределены приоритеты между логическими операциями и как определяется название сложной формулы.Содержание книги
Поиск на нашем сайте
Как распределены приоритеты между логическими операциями и как определяется название сложной формулы? Приоритеты по убывающей: отрицание (инверсия), конъюнкцию (от лат. conjunctio – союз, связь; логическое умножение), дизъюнкцию (от лат. disjunctio – различие, разделение; логическое сложение), импликацию (от лат.implico – тесная связь), и эквиваленцию (от лат. aequivalens – равносильный, равноценный). Каков порядок составления таблицы истинности для сложной формулы? Сначала нужно определить приоритеты выполнения операций. Затем, исходя из количества простых высказываний, входящих в сложное высказывание, выписывают всевозможное комбинации логических значений этих высказываний. Количество комбинаций определяет число строк таблицы истинности, и для двоичных комбинаций оно равно Количество столбцов таблицы истинности определяется суммой чисел последовательно выполняемых операций и простых высказываний. Запишите аксиомы одиночных элементов (1-я группа аксиом). Аксиомы одиночных элементов: 1) 3) Запишите аксиомы и законы отрицания (2-я группа аксиом). Аксиомы и законы отрицания: 1)
4) Запишите комбинационные законы алгебры логики (3-я группа аксиом). Комбинационные законы: 1) 2)
 – сочетательные – сочетательные
В чем суть полноты систем логических операций? Приведите 3 функционально полные системы операций. Отметим еще одно чрезвычайно важное свойство функциональной полноты системы операций. Если любую формулу алгебры логики можно свести к некоторой другой равносильной формуле, содержащей только определенную систему операций, то такая система операций называется функционально полной системой операций (ФПСО) или базисной. В алгебре логики такой ФПСО являются системы операций: Правила склеивания для элементарных конъюнкций и дизъюнкций. Примеры. Сначала введем некоторые понятия. Логическое произведение Например:
Количество сомножителей в элементарном произведении называется его рангом. Два элементарных произведения одинакового ранга Теперь сформулируем само правило склеивания для элементарных конъюнкций: логическую сумму двух соседних произведений некоторого ранга Пример: Аналогично для дизъюнкции определяются ранг и соседство. Правило склеивания для элементарных дизъюнкций формулируется следующим образом: логическое произведение двух соседних дизъюнкций ранга Пример: Правила поглощения для элементарных конъюнкций и дизъюнкций. Примеры. Логическую сумму двух элементарных конъюнкций разных рангов, из которых одна является частью другой, можно заменить слагаемым, имеющим меньший ранг. Пример: Правило поглощения для элементарных дизъюнкций формулируется следующим образом: логическое произведение двух элементарных дизъюнкций разных рангов, одна из которых является частью другой, можно заменить сомножителем меньшего ранга. Пример: Правила склеивания и поглощения, как нетрудно заметить, являются следствием распределительных законов. Правило развертывания для элементарных конъюнкций и дизъюнкций. Примеры. Что такое НДФ, СНДФ, НКФ и СНКФ? Примеры. В алгебре логики каноническими принято считать нормальную дизъюнктивную форму (НДФ) и нормальную конъюнктивную форму (НК Ф) и соответственно совершенную НДФ (СНДФ) и совершенную НКФ (СНКФ). Как распределены приоритеты между логическими операциями и как определяется название сложной формулы? Приоритеты по убывающей: отрицание (инверсия), конъюнкцию (от лат. conjunctio – союз, связь; логическое умножение), дизъюнкцию (от лат. disjunctio – различие, разделение; логическое сложение), импликацию (от лат.implico – тесная связь), и эквиваленцию (от лат. aequivalens – равносильный, равноценный).
|
||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 161; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.227.108 (0.007 с.) |

 , где
, где  – число различных простых высказываний.
– число различных простых высказываний. ; 2)
; 2)  ;
; ; 4)
; 4)  .
. ; 2)
; 2)  (закон противоречия);3)
(закон противоречия);3)  (закон исключенного третьего);
(закон исключенного третьего); ; 5)
; 5)  (законы де Моргана).
(законы де Моргана). (общий случай
(общий случай  );
);  законы идемпотентности
законы идемпотентности (общий случай
(общий случай  );
); – переместительные законы;
– переместительные законы; .
. сумма любого числа высказываний называется элементарным, если сомножители
сумма любого числа высказываний называется элементарным, если сомножители  – элементарное произведение,
– элементарное произведение, – неэлементарное произведение.
– неэлементарное произведение. называются соседними, если они являются формулами одних и тех же высказываний и отличаются знаком отрицания только одного высказывания.
называются соседними, если они являются формулами одних и тех же высказываний и отличаются знаком отрицания только одного высказывания.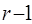 , являющимся общей частью исходных слагаемых.
, являющимся общей частью исходных слагаемых.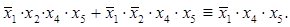
 , являющейся общей частью исходных сомножителей.
, являющейся общей частью исходных сомножителей.

 .
.


