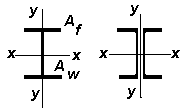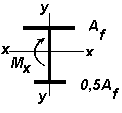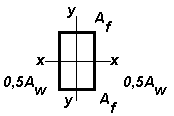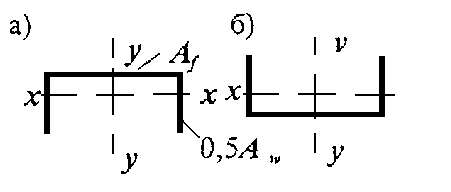Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Сталь прокатная широкополосная, универсальная по ГОСТу 82-70
Таблица 16, б
| Ширина, мм
| Масса 1 м полосы, кг при толщине, мм
| |
|
|
|
|
|
| |
| 39,25
41,21
43,18
47,10
49,06
51,03
54,95
58,88
62,80
66,73
70,65
74,58
78,50
82,43
88,31
94,20
98,13
104,01
109,90
117,75
123,64
127,56
131,50
137,38
147,19
157,00
166,81
176,63
186,44
196,25
206,06
| 43,96
46,16
48,36
52,75
54,95
57,15
61,54
65,94
70,34
74,73
79,13
83,52
87,92
92,32
98,91
105,50
109,90
116,49
123,08
131,88
138,47
142,87
147,40
153,86
164,85
175,84
186,83
197,82
208,81
219,80
230,79
| 47,10
49,46
51,81
56,52
58,88
61,23
65,94
70,65
75,36
80,07
84,78
89,49
94,20
98,91
105,98
113,04
117,75
124,82
131,88
141,30
148,37
153,08
157,78
164,85
176,63
188,40
200,18
211,95
223,73
235,50
247,28
| 50,24
52,75
55,26
60,29
62,80
65,31
70,34
75,36
80,38
85,41
90,43
95,46
100,48
105,50
113,04
120,55
125,60
133,14
140,67
150,72
158,26
163,28
168,40
175,84
188,40
200,96
213,52
226,08
238,64
251,20
263,76
| 56,52
59,35
62,17
67,82
70,65
73,48
79,13
84,78
90,43
96,08
101,74
107,39
113,04
118,69
127,17
135,65
141,30
149,78
158,25
169,56
178,04
183,69
189,40
197,82
211,95
226,08
240,21
254,34
268,47
282,60
296,73
| 62,80
65,94
69,08
75,36
78,50
81,64
87,92
94,20
100,48
106,76
113,04
119,32
125,60
131,88
141,30
150,72
157,00
166,42
175,84
188,40
197,82
204,10
210,36
219,80
235,50
251,20
266,90
282,60
298,30
314,00
329,70
|
Проверить все геометрическме характеристики
Равнополочныеуголки (выборкаиз ГОСТ 8509-86)

Таблица 17
| Размер уголка,мм
| А, см2
| Масса 1 м, кг
| z0, см
| Ix
cм4
| ix
cм
| Радиус инерцииiy2 для двух уголков при δ, мм
| | b
| t
|
|
| |
|
| 3,48
4,29
| 2,73
3,37
| 1,26
1,3
| 6,63
8,03
| 1,38
1,37
| 2,16
2,18
| 2,24
2,26
| | 50*
|
5*
| 3,89
4,8
| 3,05
3,77
| 1,38
1,42
| 9,21
11,2
| 1,54
1,53
| 2,35
2,38
| 2,43
2,45
| |
|
| 4,38
5,41
| 3,44
4,25
| 1,52
1,57
| 13,1
| 1,73
1,72
| 2,58
2,61
| 2,66
2,72
| | 63*
|
5*
| 4,96
6,13
7,28
| 3,9
4,81
5,72
| 1,69
1,74
1,78
| 18,9
23,1
27,1
| 1,95
1,94
1,93
| 2,86
2,89
2,9
| 2,93
2,96
2,99
| | 70*
| 4,5
5*
6*
| 6,2
6,86
8,15
9,42
10,7
| 4,87
5,38
6,39
7,39
8,37
| 1,88
1,9
1,94
1,99
2,02
|
31,9
37,6
48,2
| 2,16
2,16
2,15
2,14
2,13
| 3,21
3,16
3,18
3,2
3,22
| 3,21
3,23
3,25
3,28
3,29
| | 75*
|
6*
| 7,39
8,78
10,1
11,5
12,8
| 5,8
6,89
7,96
9,02
10,1
| 2,02
2,06
2,1
2,15
2,18
| 39,5
46,6
53,3
59,8
66,1
| 2,31
2,3
2,29
2,28
2,27
| 3,35
3,3
3,4
3,43
3,44
| 3,42
3,44
3,47
3,5
3,51
| | 80*
| 5,5
7*
| 8,63
9,38
10,8
12,3
| 6,78
7,36
8,51
6,65
| 2,17
2,19
2,23
2,27
| 52,7
65,3
73,4
| 2,47
2,47
2,45
2,44
| 3,57
3,58
3,6
3,62
| 3,64
3,65
3,67
3,69
| | 90*
| 6*
7*
| 10,6
12,3
13,9
15,6
| 8,33
9,64
10,9
12,2
| 2,43
2,47
2,51
2,55
| 82,1
94,3
| 2,78
2,77
2,76
2,75
| 3,96
3,99
4,01
4,04
| 4,04
4,06
4,08
4,11
| | 100*
| 6,5
7*
8*
| 12,8
13,8
15,5
19,2
22,8
26,3
29,7
| 10,1
10,8
12,2
15,1
17,9
20,6
23,3
| 2,68
2,71
2,75
2,83
2,91
2,99
3,06
|
| 3,09
3,08
3,07
3,05
3,03
2,98
| 4,36
4,38
4,47
4,44
4,48
4,53
4,64
| 4,43
4,45
4,54
4,52
4,56
4,6
4,72
| | 110*
|
8*
| 15,2
17,2
| 11,9
13,5
| 2,96
3,0
|
| 3,4
3,39
| 4,78
4,8
| 4,85
4,87
| | 125*
| 8*
9*
| 19,7
24,3
28,9
33,4
37,8
| 15,5
17,3
19,1
22,7
26,2
29,6
| 3,36
3,4
3,45
3,53
3,61
3,68
|
| 3,87
3,86
3,85
3,82
3,8
3,78
| 5,39
5,41
5,44
5,48
5,52
5,66
| 5,46
5,48
5,52
5,55
5,6
5,72
| | 140*
| 9*
10*
| 24,7
27,3
32,5
| 19,4
21,5
25,5
| 3,78
3,82
3,9
|
| 4,34
4,33
4,31
| 6,02
6,05
6,08
| 6,1
6,12
6,15
| | 160*
| 10*
11*
| 31,4
34,4
37,4
43,3
49,1
54,8
60,4
| 24,7
29,4
38,5
47,4
| 4,3
4,35
4,39
4,47
4,55
4,63
4,7
|
| 4,96
4,95
4,94
4,92
4,89
4,87
4,85
| 6,84
6,86
6,88
6,91
6,95
7,04
| 6,91
6,93
6,95
6,98
7,03
7,07
7,11
| | 180*
| 11*
12*
| 38,8
42,2
| 30,5
33,1
| 4,85
4,89
|
| 5,6
5,59
| 7,67
7,69
| 7,74
7,76
| | 200*
| 12*
14*
20*
30*
| 47,1
50,9
54,6
76,5
94,3
111,5
|
39,9
42,8
48,7
60,1
87,6
| 5,37
5,42
5,46
5,54
5,7
5,89
6,07
|
| 6,22
6,21
6,2
6,17
6,12
6,06
| 8,48
8,5
8,52
8,56
8,65
8,74
8,83
| 8,55
8,58
8,6
8,64
8,72
8,81
8,9
| | 220*
| 14*
16*
| 60,4
68,6
| 47,4
53,8
| 5,93
6,02
|
| 6,83
6,81
| 9,31
9,35
| 9,37
9,42
| | 250*
| 16*
20*
| 78,4
87,7
106,1
119,7
138,1
| 61,5
68,9
76,1
83,3
104,5
111,4
| 6,75
6,83
6,91
7,11
7,23
7,31
|
| 7,76
7,73
7,71
7,69
7,65
7,61
7,59
| 10,55
10,59
10,62
10,67
10,72
10,78
10,82
| 10,62
10,65
10,69
10,74
10,79
10,85
10,89
|
Приведенные гибкости стержней сквозного сечения
Таблица 18 (т. 1.4.2, [1])
| Сечение сквозного стержня
| Приведенная гибкость ef стержня сквозного сечения
| | тип
| схема
| с планками
| с решетками
| |
|

| 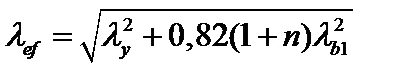 (1.4.8)
(1.4.8)
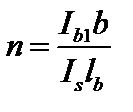
|  (1.4.11)
(1.4.11)
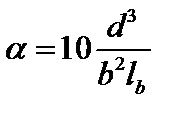 (d1, d2 относится соответственно к сторонам b1, b2)
(d1, d2 относится соответственно к сторонам b1, b2)
| |
|

| 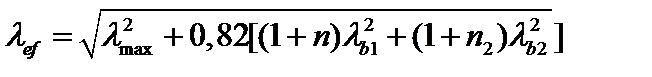 (1.4.9)
(1.4.9)
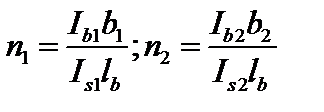
|  (1.4.12)
(1.4.12)

| |
| 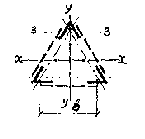
| 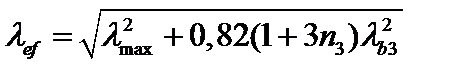 (1.4.10)
(1.4.10)
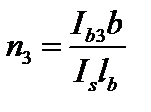
|  (1.4.13)
(1.4.13)

| Обозначения, принятые в табл.1.4.2:
 – гибкость сквозного стержня в плоскости, перпендикулярной к осиі y – y; – гибкость сквозного стержня в плоскости, перпендикулярной к осиі y – y;
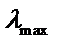 – наибольшая из гибкостей сквозного стержня в плоскостях, перпендикулярных к осям x – x или y – y, что равняется соответственно – наибольшая из гибкостей сквозного стержня в плоскостях, перпендикулярных к осям x – x или y – y, что равняется соответственно  или или 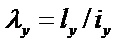 (где ix , iy – радиусы инерции сечения сквозного стержня в целом); (где ix , iy – радиусы инерции сечения сквозного стержня в целом);
 , , 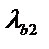 , ,  – гибкости отдельных веток при изгибе в плоскостях, перпендикулярных к осям соответственно 1 – 1, 2 – 2 и 3 – 3 на участках промежуточными связями (сварными швами или крайними болтами, что крепят планки);
b, d, lb – геометрические размеры сквозного стержня, что определяются по рис. 1.4.2 і 1.4.3;
А – площадь поперечного сечения всего стержня;
Аd1, Аd2, Аd3 – площади поперечных сечений раскосов решеток (при крестовой решетке – двух раскосов), размещенных соответственно в плоскостях, перпендикулярным осям 1 - 1, 2 - 2 и параллельных к оси 3 - 3;
Ib1, Ib3 – моменты инерции веток относительно осей 1 – 1 і 3 – 3 (для сечений типов 1 і 3);
Ib1, Ib2 – то же самое, двух уголоков относительно осей 1 – 1 і 2 – 2 (для сечения типа 2);
Is – момент инерции поперечного сечения одной планки относительно собственной оси х – х (рис. 1.4.3; для сечений типов 1 і 3);
Is1, Is2 – моменты инерции сечения одной из планок, размещенных в плоскостях соответственно 1 – 1 і 2 – 2 (для сечения типа 2).
Примечание
К типу сечения 1 следует относить также сечения, в которых вместо швеллеров используются двутавры, трубчатые и др. профили для одной или двух веток, при этом оси y – y і 1 – 1 должны проходить через центры тяжести относительно сечения в целом и отдельной ветки, а значения n і – гибкости отдельных веток при изгибе в плоскостях, перпендикулярных к осям соответственно 1 – 1, 2 – 2 и 3 – 3 на участках промежуточными связями (сварными швами или крайними болтами, что крепят планки);
b, d, lb – геометрические размеры сквозного стержня, что определяются по рис. 1.4.2 і 1.4.3;
А – площадь поперечного сечения всего стержня;
Аd1, Аd2, Аd3 – площади поперечных сечений раскосов решеток (при крестовой решетке – двух раскосов), размещенных соответственно в плоскостях, перпендикулярным осям 1 - 1, 2 - 2 и параллельных к оси 3 - 3;
Ib1, Ib3 – моменты инерции веток относительно осей 1 – 1 і 3 – 3 (для сечений типов 1 і 3);
Ib1, Ib2 – то же самое, двух уголоков относительно осей 1 – 1 і 2 – 2 (для сечения типа 2);
Is – момент инерции поперечного сечения одной планки относительно собственной оси х – х (рис. 1.4.3; для сечений типов 1 і 3);
Is1, Is2 – моменты инерции сечения одной из планок, размещенных в плоскостях соответственно 1 – 1 і 2 – 2 (для сечения типа 2).
Примечание
К типу сечения 1 следует относить также сечения, в которых вместо швеллеров используются двутавры, трубчатые и др. профили для одной или двух веток, при этом оси y – y і 1 – 1 должны проходить через центры тяжести относительно сечения в целом и отдельной ветки, а значения n і 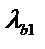 в формуле (1.4.8) должны обеспечить наибольшее значение приведенной гибкости в формуле (1.4.8) должны обеспечить наибольшее значение приведенной гибкости 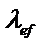 . .
| Коэффициенты устойчивости je при внецентренном сжатии сквозных стержней в плоскости действия момента, совпадающей с плоскостью симметрии
Таблица 19 (т. К.4, Приложения [1])
Условная приведенная гибкость 
| Значение je при значении относительного
эксцентриситета m
| | 0,1
| 0,25
| 0,5
| 0,75
| 1,0
| 1,25
| 1,5
| 1,75
| 2,0
| | 0,5
|
|
|
|
|
|
|
|
|
| | 1,0
|
|
|
|
|
|
|
|
|
| | 1,5
|
|
|
|
|
|
|
|
|
| | 2,0
|
|
|
|
|
|
|
|
|
| | 2,5
|
|
|
|
|
|
|
|
|
| | 3,0
|
|
|
|
|
|
|
|
|
| | 3,5
|
|
|
|
|
|
|
|
|
| | 4,0
|
|
|
|
|
|
|
|
|
| | 4,5
|
|
|
|
|
|
|
|
|
| | 5,0
|
|
|
|
|
|
|
|
|
| | 5,5
|
|
|
|
|
|
|
|
|
| | 6,0
|
|
|
|
|
|
|
|
|
| | 6,5
|
|
|
|
|
|
|
|
|
| | 7,0
|
|
|
|
|
|
|
|
|
| | 8,0
|
|
|
|
|
|
|
|
|
| | 9,0
|
|
|
|
|
|
|
|
|
| | 10,0
|
|
|
|
|
|
|
|
|
| | 11,0
|
|
|
|
|
|
|
|
|
| | 12,0
|
|
|
|
|
|
|
|
|
| | 13,0
|
|
|
|
|
|
|
|
|
| | 14,0
|
|
|
|
|
|
|
|
|
|
Продолжение таблицы 19 (т. К.4, Приложения [1])
Условная приведенная гибкость 
| Значение je при значении относительного
эксцентриситета m
| | 2,5
| 3,0
| 3,5
| 4,0
| 4,5
| 5,0
| 5,5
| 6,0
| 6,5
| | 0,5
|
|
|
|
|
|
|
|
|
| | 1,0
|
|
|
|
|
|
|
|
|
| | 1,5
|
|
|
|
|
|
|
|
|
| | 2,0
|
|
|
|
|
|
|
|
|
| | 2,5
|
|
|
|
|
|
|
|
|
| | 3,0
|
|
|
|
|
|
|
|
|
| | 3,5
|
|
|
|
|
|
|
|
|
| | 4,0
|
|
|
|
|
|
|
|
|
| | 4,5
|
|
|
|
|
|
|
|
|
| | 5,0
|
|
|
|
|
|
|
|
|
| | 5,5
|
|
|
|
|
|
|
|
|
| | 6,0
|
|
|
|
|
|
|
|
|
| | 6,5
|
|
|
|
|
|
|
|
|
| | 7,0
|
|
|
|
|
|
|
|
|
| | 8,0
|
|
|
|
|
|
|
|
|
| | 9,0
|
|
|
|
|
|
|
|
|
| | 10,0
|
|
|
|
|
|
|
|
|
| | 11,0
|
|
|
|
|
|
|
|
|
| | 12,0
|
|
|
|
|
|
|
|
|
| | 13,0
|
|
|
|
|
|
|
|
|
| | 14,0
|
|
|
|
|
|
|
|
|
| Окончание таблицы 19 (т. К.4, Приложения [1])
Условная приведенная гибкость 
| Значение je при значении относительного
эксцентриситета m
| | 7,0
| 8,0
| 9,0
|
|
|
|
|
| | 0,5
|
|
|
|
|
|
|
|
| | 1,0
|
|
|
|
|
|
|
|
| | 1,5
|
|
|
|
|
|
|
|
| | 2,0
|
|
|
|
|
|
|
|
| | 2,5
|
|
|
|
|
|
|
|
| | 3,0
|
|
|
|
|
|
|
|
| | 3,5
|
|
|
|
|
|
|
|
| | 4,0
|
|
|
|
|
|
|
|
| | 4,5
|
|
|
|
|
|
|
|
| | 5,0
|
|
|
|
|
|
|
|
| | 5,5
|
|
|
|
|
|
|
|
| | 6,0
|
|
|
|
|
|
|
|
| | 6,5
|
|
|
|
|
|
|
|
| | 7,0
|
|
|
|
|
|
|
|
| | 8,0
|
|
|
|
|
|
|
|
| | 9,0
|
|
|
|
|
|
|
|
| | 10,0
|
|
|
|
|
|
|
|
| | 11,0
|
|
|
|
|
|
|
|
| | 12,0
|
|
|
|
|
|
|
|
| | 13,0
|
|
|
|
|
|
|
|
| | 14,0
|
|
|
|
|
|
|
|
| | Примечания:
1. Значения коэффициентов je в таблице увеличены в 1000 раз.
2. Значение коэффициента je следует принимать не более за значение коэффициента j.
|
Коэффициенты для расчета элементов с учетом развития пластических деформаций
Таблица 20 (т Н.1, Приложения [1])
| Тип сечения
| Схема сечения
| Af / Aw
| Наибольшее значение коэффициентов
| | сх
| сy
| n при Му = 01)
| |
| 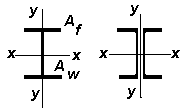
| 0,25
| 1,19
| 1,47
| 1,5
| | 0,50
| 1,12
| | 1,00
| 1,07
| | 2,00
| 1,04
| |
| 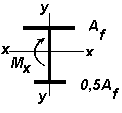
| 0,5
| 1,40
| 1,47
| 2,0
| | 1,0
| 1,28
| | 2,0
| 1,18
| |
| 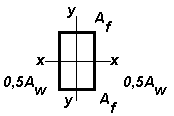
| 0,25
0,50
1,00
2,00
| 1,19
1,12
1,07
1,04
| 1,07
1,12
1,20
1,26
| 1,5
| |
| 
| 0,50
1,00
2,00
| 1,40
1,28
1,18
| 1,12
1,20
1,31
| 2,0
| |
| 
| —
| 1,47
| 1,47
| а) 2,0
б) 3,0
| |
| 
| 0,25
0,50
1,00
2,00
| 1,47
| 1,04
1,07
1,12
1,19
| 3,0
| |
| 
| –
| 1,26
| 1,26
| 1,5
| |
| 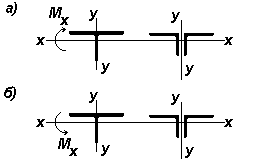
| –
| 1,60
| l,47
| a) 3,0
б) 1,0
| |
| 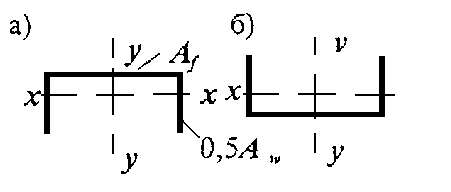
| 0,5
1,0
2,0
| 1,6
| 1,07
1,12
1,19
| a) 3,0
б) 1,0
| | 1) При My ¹ 0 принимается n = 1,5, за исключением сечений типу 5, а, для которого n = 2, и типа 5, б, для якоторого n = 3.
Примечания:
1. При определении коэффициентов для промежуточных значений Аf / Aw допускается линейная интерполяция.
2. Значения коэффициентов сх и сy следует принимать не более чем 1,15 gf, где gf – коэффициент надежности по нагрузке, вычисленный як отношение расчетного значения эквивалентного (по значениям изгибающего момента) нагрузки к характеристическому.
|
|





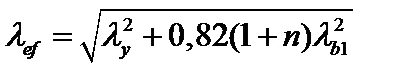 (1.4.8)
(1.4.8)
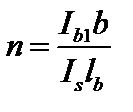
 (1.4.11)
(1.4.11)
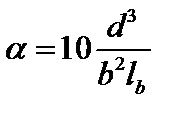 (d1, d2 относится соответственно к сторонам b1, b2)
(d1, d2 относится соответственно к сторонам b1, b2)

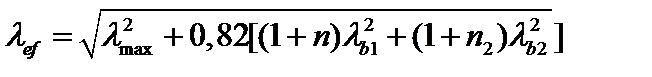 (1.4.9)
(1.4.9)
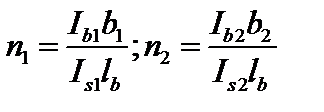
 (1.4.12)
(1.4.12)

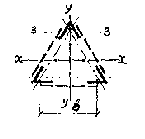
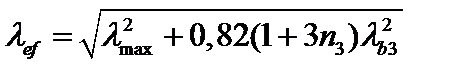 (1.4.10)
(1.4.10)
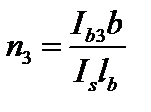
 (1.4.13)
(1.4.13)

 – гибкость сквозного стержня в плоскости, перпендикулярной к осиі y – y;
– гибкость сквозного стержня в плоскости, перпендикулярной к осиі y – y;
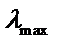 – наибольшая из гибкостей сквозного стержня в плоскостях, перпендикулярных к осям x – x или y – y, что равняется соответственно
– наибольшая из гибкостей сквозного стержня в плоскостях, перпендикулярных к осям x – x или y – y, что равняется соответственно  или
или 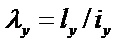 (где ix , iy – радиусы инерции сечения сквозного стержня в целом);
(где ix , iy – радиусы инерции сечения сквозного стержня в целом);
 ,
, 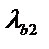 ,
,  – гибкости отдельных веток при изгибе в плоскостях, перпендикулярных к осям соответственно 1 – 1, 2 – 2 и 3 – 3 на участках промежуточными связями (сварными швами или крайними болтами, что крепят планки);
b, d, lb – геометрические размеры сквозного стержня, что определяются по рис. 1.4.2 і 1.4.3;
А – площадь поперечного сечения всего стержня;
Аd1, Аd2, Аd3 – площади поперечных сечений раскосов решеток (при крестовой решетке – двух раскосов), размещенных соответственно в плоскостях, перпендикулярным осям 1 - 1, 2 - 2 и параллельных к оси 3 - 3;
Ib1, Ib3 – моменты инерции веток относительно осей 1 – 1 і 3 – 3 (для сечений типов 1 і 3);
Ib1, Ib2 – то же самое, двух уголоков относительно осей 1 – 1 і 2 – 2 (для сечения типа 2);
Is – момент инерции поперечного сечения одной планки относительно собственной оси х – х (рис. 1.4.3; для сечений типов 1 і 3);
Is1, Is2 – моменты инерции сечения одной из планок, размещенных в плоскостях соответственно 1 – 1 і 2 – 2 (для сечения типа 2).
Примечание
К типу сечения 1 следует относить также сечения, в которых вместо швеллеров используются двутавры, трубчатые и др. профили для одной или двух веток, при этом оси y – y і 1 – 1 должны проходить через центры тяжести относительно сечения в целом и отдельной ветки, а значения n і
– гибкости отдельных веток при изгибе в плоскостях, перпендикулярных к осям соответственно 1 – 1, 2 – 2 и 3 – 3 на участках промежуточными связями (сварными швами или крайними болтами, что крепят планки);
b, d, lb – геометрические размеры сквозного стержня, что определяются по рис. 1.4.2 і 1.4.3;
А – площадь поперечного сечения всего стержня;
Аd1, Аd2, Аd3 – площади поперечных сечений раскосов решеток (при крестовой решетке – двух раскосов), размещенных соответственно в плоскостях, перпендикулярным осям 1 - 1, 2 - 2 и параллельных к оси 3 - 3;
Ib1, Ib3 – моменты инерции веток относительно осей 1 – 1 і 3 – 3 (для сечений типов 1 і 3);
Ib1, Ib2 – то же самое, двух уголоков относительно осей 1 – 1 і 2 – 2 (для сечения типа 2);
Is – момент инерции поперечного сечения одной планки относительно собственной оси х – х (рис. 1.4.3; для сечений типов 1 і 3);
Is1, Is2 – моменты инерции сечения одной из планок, размещенных в плоскостях соответственно 1 – 1 і 2 – 2 (для сечения типа 2).
Примечание
К типу сечения 1 следует относить также сечения, в которых вместо швеллеров используются двутавры, трубчатые и др. профили для одной или двух веток, при этом оси y – y і 1 – 1 должны проходить через центры тяжести относительно сечения в целом и отдельной ветки, а значения n і 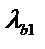 в формуле (1.4.8) должны обеспечить наибольшее значение приведенной гибкости
в формуле (1.4.8) должны обеспечить наибольшее значение приведенной гибкости 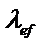 .
.