Построение внутреннего сопряжения.

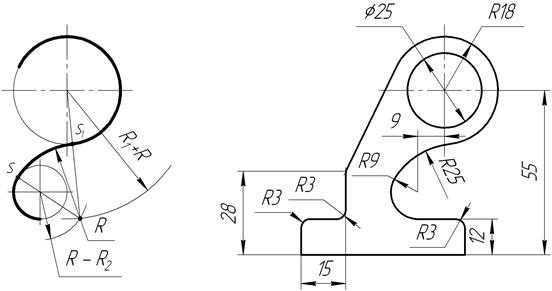
Задано:

а) радиусы сопрягаемых окружностей R₁ и R₂;

б) расстояние l₁ и l₂ между центрами этих дуг;

в) радиус R сопрягающей дуги.

Требуется:

а) определить положение центра О₂ сопрягающей дуги;

б) найти точки сопряжения S и S₁;

в) провести дугу сопряжения.

Построение сопряжения показано на рисунке 40а. По заданным расстояниям между центрами l₁ и l₂ на чертеже намечают центры О и О₁, из которых описывают сопрягаемые дуги радиусов R₁ и R₂. Из центра О₁ проводят вспомогательную дугу окружности радиусом, равным разности радиусов сопрягающей дуги R и сопрягаемой R₂, а из центра О – радиусом, равным разности радиусов сопрягающей дуги R и сопрягаемой R₁. Вспомогательные дуги пересекутся в точке О₂, которая и будет искомым центром сопрягающей дуги.

Для нахождения точек сопряжения точку О₂ соединяют с точками О и О₁ прямыми линиями. Точки пересечения продолжения прямых О₂О и О₂О₁ с сопрягаемыми дугами являются искомыми точками сопряжения (точки S и S₁).

Радиусом R из центра О₂ проводят сопрягающую дугу между точками сопряжения S и S₁.

Построение внешнего сопряжения.

Задано:

а) радиусы R₁ и R₂ сопрягаемых дуг окружностей;

б) расстояние l₁ и l₂ между центрами этих дуг;

в) радиус R сопрягающей дуги.

Требуется:

а) определить положение центра О₂ сопрягающей дуги;

б) найти точки сопряжения S и S₁;

в) провести дугу сопряжения.

Построение внешнего сопряжения показано на рисунке 40б. По заданным расстояниям между центрами l₁ и l₂ на чертеже намечают центры О и О₁, из которых описывают сопрягаемые дуги радиусов R₁ и R₂. Из центра О проводят вспомогательную дугу окружности радиусом, равным сумме радиусов сопрягаемой дуги R₁ и сопрягающей R, а из центра О₁ – радиусом, равным сумме радиусов сопрягаемой R₂ и сопрягающей R. Вспомогательные дуги пересекутся в точке О₂, которая и будет искомым центром сопрягающей дуги.

Для нахождения точек сопряжения центры дуг соединяют прямыми линиями ОО₂ и О₁О₂. Эти две прямые пересекают сопрягаемые дуги в точках сопряжения S и S1.

Из центра О₂ радиусом R проводят сопрягающую дугу, ограничивая её точками сопряжения S и S₁.

Построение смешанного сопряжения.

Задано:

а) радиусы R₁ и R₂ сопрягаемых дуг окружностей;

б) расстояние l₁ и l₂ между центрами этих дуг;

в) радиус R сопрягающей дуги.

Требуется:

а) определить положение центра О₂ сопрягающей дуги;

б) найти точки сопряжения S и S₁;

в) провести дугу сопряжения.

Пример смешанного сопряжения приведен на рисунке 41 а,б.

 

а) б)

Рисунок 41 – Построение сопряжений

 

По заданным расстояниям между центрами l₁ и l₂ на чертеже намечают центры О и О₁, из которых описывают сопрягаемые дуги радиусов R₁ и R₂. Из центра О проводят вспомогательную дугу окружности радиусом, равным сумме радиусов сопрягаемой дуги R₁ и сопрягающей R, а из центра О₁ – радиусом, равным разности радиусов R и R₂. Вспомогательные дуги пересекутся в точке О₂, которая и будет искомым центром сопрягающей дуги.

Соединив точки О и О₂ прямой получают точку сопряжения S₁, соединив точки О₁ и О₂ находят точку сопряжения S. Из центра О₂ проводят дугу сопряжения от S до S₁.

 

 

Таблица 6 – Варианты графической работы на построение сопряжений

 

1	2
3	4
5	6
7	8

 

Продолжение таблицы 6

9	10
11	12
13	14
15	16

Продолжение таблицы 6

17	18
19	20
21	22

 

Продолжение таблицы 6

23	24
25	26
28	29

 

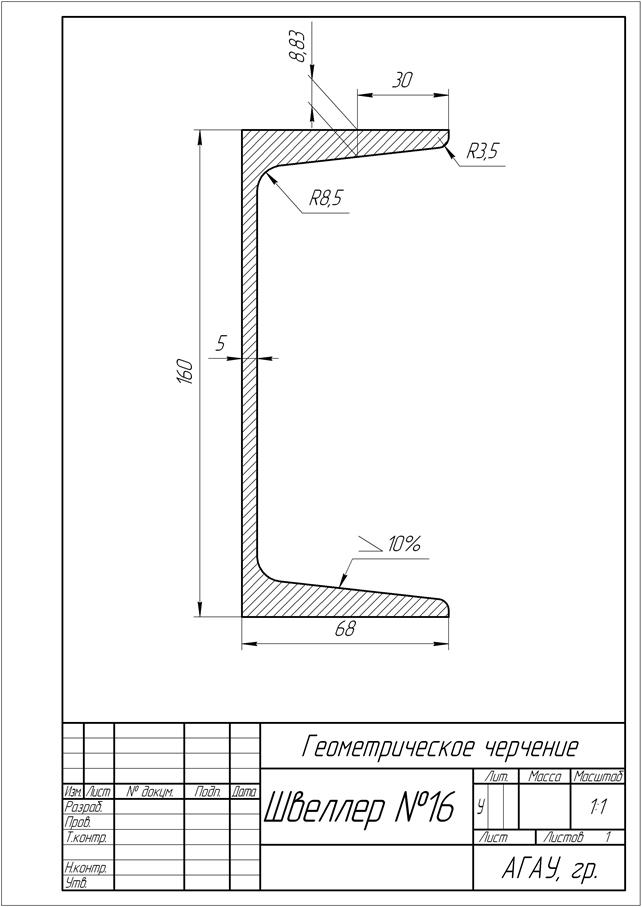
УСЛОВНЫЕ ЗНАКИ ЧЕРТЕЖА

ПОСТРОЕНИЕ УКЛОНА

Лист № 5

Цель задания: ознакомление с условными знаками, применяемыми в черчении для упрощения чтения чертежа. Правила построения уклона.

Выполнить:

1. на листе формата А4 вычертить профиль прокатной стали по своему варианту (таблица 7);

2. проставить цифровые значения размеров.

Пример выполнения профиля прокатной стали показан на стр. 44.

Данные для выбранного профиля берутся из справочника по машиностроительному черчению, авторы В.А.Федоренко и А.И.Шошин.

 

Плоские поверхности, расположенные под небольшим углом, часто характеризуют величиной уклона.

Уклоном «i» прямой АВ относительно прямой АС называют отношение разности высот двух точек С и В к горизонтальному расстоянию между ними, т.е. отношение катета ВС к катету АС (рисунок 42). Уклон обозначают на чертежах знаком Ð, который наносят перед размерным числом, характеризующим уклон. При этом острый угол направляют в сторону наклона поверхности.

 

Рисунок 42 – Уклон

 

Уклоны обычно выражают простой дробью или в процентах (рисунок 43).

 

 

Рисунок 43 – Обозначение уклона

Уклоны применяются при вычерчивании деталей, например стальных балок и рельсов, изготовляемых на прокатных станках, и некоторых деталей, изготовленных литьём.

 

Таблица 7 – Варианты графической работы на построение уклона

 

Вариант	Профиль прокатной стали	Вариант	Профиль прокатной стали
	Балка двутавровая № 10		Швеллер № 22
	Швеллер № 12		Балка двутавровая № 20
	Балка двутавровая № 24		Швеллер № 14а
	Балка двутавровая № 12		Швеллер № 24
	Швеллер № 14		Балка двутавровая № 18а
	Балка двутавровая № 24а		Швеллер № 16а
	Балка двутавровая № 14		Швеллер № 24а
	Швеллер № 16		Балка двутавровая № 20а
	Швеллер № 20а		Швеллер № 18а
	Балка двутавровая № 16		Балка двутавровая № 22а
	Швеллер № 18		Швеллер № 10
	Швеллер № 22а		Балка двутавровая № 22
	Балка двутавровая № 18		Швеллер № 27
	Швеллер № 20		Швеллер № 8

 

Примечание: предметы или элементы, имеющие постоянное или закономерно изменяющееся поперечное сечение (валы, цепи, прутки, фасонный прокат, шатуны и т.п.), допускается изображать с разрывами (рисунок 44).

Частичные изображения и изображения с разрывами ограничивают сплошной волнистой линией, соединяющей соответствующие линии контура.

 

 

Рисунок 44

КОНУСНОСТЬ

 

Лист № 6

Цель задания: ознакомление с условными знаками, применяемыми в черчении для упрощения чтения чертежа. Правила построения конусности и фасок под различными углами.

Выполнить:

1. на листе формата А4 выполнить задание «Цапфа». Масштаб 1:1.

2. проставить цифровые значения размеров.

Все размеры для данного задания необходимо взять из таблицы 8 по своему варианту.

 

Цапфа – это часть вала или оси, опирающаяся на подшипник. Ось цапфы располагают горизонтально.

Под конусностью понимают отношение диаметра основания конуса к его высоте, т.е. D/L, а для усечённого конуса - отношение разности диаметров оснований конуса к расстоянию между ними (рисунок 45).

 

 

Рисунок 45 – Конусность

 

По ГОСТ 2.307- 68 конусность обозначают знаком «», который ставят перед размерным числом, характеризующим конусность. Условный знак конусности имеет вид равнобедренного треугольника, острый угол знака направляют в сторону вершины конуса, а значение располагают параллельно его оси над полкой линии-носки или над осевой линией (рисунок 46).

 

Рисунок 46 – Обозначение конусности

ОБОЗНАЧЕНИЕ ФАСОК

 

Многие детали имеют фаски – небольшие конические или пирамидальные поверхности. Если фаска снята под углом 45º, то её размер записывают условной надписью, первая цифра которой указывает высоту фаски (высоту усеченного конуса), а вторая цифра – угол наклона образующей конуса к его основанию, например 2 × 45º (рисунок 47).

 

 

Рисунок 47 – Примеры нанесения размеров фаски

 

Если фаска имеет угол, отличный от 45º, то её размер указывают по общим правилам – двумя линейными размерами (рисунок 48, а) или линейным и угловым размерами (рисунок 48 б, в).

 

а) б) в)

 

Рисунок 48 – Примеры нанесения размеров фаски

В случаях, когда деталь имеет две симметрично расположенные одинаковые фаски на одинаковых диаметрах, размер фаски наносят один раз, без указания их числа (рисунок 49 а). Если деталь имеет несколько одинаковых фасок на цилиндрической или конической поверхности разного диаметра, то наносят размер фаски только один раз, с указанием их числа (рисунок 49 б).

 

а) б)

 

Рисунок 49 – Примеры нанесения размеров фаски

 

 

Примечание: предметы или элементы, имеющие постоянное или закономерно изменяющееся поперечное сечение (валы, цепи, прутки, фасонный прокат, шатуны и т.п.), допускается изображать с разрывами (рисунок 50).

Частичные изображения и изображения с разрывами ограничивают сплошной волнистой линией, соединяющей соответствующие линии контура.

 

 

 

Рисунок 50

Цапфа

 

Таблица 8 – Данные к заданию «Цапфа»

 

вариант	L	l	D	b	a	n	c	aº
							2.0
							2.0
							2.0
							2.5
							2.5
							2.5
							2.5
							2.5
							3.0
							3.0
							3.0
							3.0
							3.0
							3.0
							4.0
							4.0
							4.0
							4.0
							4.0
							4.0
							5.0
							5.0
							5.0
							5.0
							5.0
							2.0
							3.0

Вопросы для самоконтроля

Форматы

1. Чем определяются размеры формата листа?

2. Какие основные форматы Вы знаете?

3. Образование дополнительных форматов чертежей.

Масштабы

4. Что называется масштабом?

5. Какие масштабы предусмотрены стандартом?

6. Какие масштабы увеличения допускается применять и как они обозначаются?

7. Как обозначаются масштабы в графе основной надписи и на поле чертежа?

Шрифты чертежные

8. Что такое размер шрифта?

9. Как определяется высота строчных букв?

10. Что определяет ширину буквы q, и какова она по отношению к размеру шрифта?

11. В зависимости от чего определяется толщина линий шрифта d?

12. Как образуется вспомогательная сетка, в которую вписывают буквы, и чем определяется шаг вспомогательной сетки?

13. Какие типы шрифтов установлены ГОСТом и как они обозначаются?

14. Какие размеры шрифта установлены ГОСТ?

15. Каковы правила написания дробей, показателей, индексов?

16. Какие размеры шрифта рекомендуются для чертежей?

17. Чему равна высота строчных букв по сравнению с прописными?

18. Подразделение шрифта в зависимости от наклона букв?

Линии

19. Какие основные типы линий применяются при выполнении чертежей?

20. В каких пределах выбирается толщина сплошной толстой основной линии?

21. Каково соотношение толщины линий одного и того же типа на одном чертеже?

22. В зависимости от чего выбирается толщина линий и наименьшее расстояние между линиями?

23. В зависимости от чего выбирается длина штрихов в штриховых и штрихпунктирных линиях?

24. Какой длины должны быть штрихи в линии?

25. Какой длины должны быть промежутки между штрихами в штрихпунктирной линии?

26. Как должны пересекаться и заканчиваться штрихпунктирные линии?

27. Какими линиями и когда можно заменять штрихпунктирные линии, применяемые в качестве центровых линий?