

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Індивідуальні домашні завдання
|
| Індивідуальне завдання № 1.1 (КФ)
Задача 1(а,б). Використовуючи метод Лагранжа, звести КФ до канонічного вигляду, указати перетворення, за допомогою якого КФ зведена до канонічного вигляду, та записати матрицю перетворення Т, указати «новий» базис, у якому КФ має канонічний вигляд, знайти ранг і індекс КФ. Чи є КФ додатньо визначеною? Виконати перевірку.
Задача 2. Використовуючи метод Якобі, звести квадратичну форму  до канонічного вигляду, знайти ранг і індекс КФ. Чи є КФ додатньо визначеною? Указати тип поверхні другого порядку до канонічного вигляду, знайти ранг і індекс КФ. Чи є КФ додатньо визначеною? Указати тип поверхні другого порядку  .
Задача 3. Використовуючи метод ортогональних перетворень, звести КФ .
Задача 3. Використовуючи метод ортогональних перетворень, звести КФ  до канонічного вигляду, указати перетворення, за допомогою якого КФ зведена до канонічного вигляду, та записати матрицю цього перетворення Т, указати «новий» базис, у якому КФ має канонічний вигляд, указати ранг і індекс КФ. Чи є КФ додатньо визначеною? Виконати перевірку. Указати тип кривої другого порядку до канонічного вигляду, указати перетворення, за допомогою якого КФ зведена до канонічного вигляду, та записати матрицю цього перетворення Т, указати «новий» базис, у якому КФ має канонічний вигляд, указати ранг і індекс КФ. Чи є КФ додатньо визначеною? Виконати перевірку. Указати тип кривої другого порядку  .
[Зб. 11, №№ 26-28] .
[Зб. 11, №№ 26-28]
| |
| Індивідуальне завдання № 1.2 (Теорія груп та кілець)
Задача 1. а) Для даної групи підстановок четвертого порядку S4 розглянути циклічну підгрупу, породжену елементом α;
б) скласти таблицю Келі множення елементів групи, указати обернені до кожного елемента групи;
в) встановити порядок даної підгрупи, індекс підгрупи у групі;
г) визначити порядок кожного елемента цієї підгрупи;
д) знайти лівий та правий розклади групи S4 за підгрупою, породженою елементом α;
е) встановити, чи є підгрупа групи нормальним дільником групи;
є) чи можливий гомоморфізм підгрупи, породженої елементом α, на групу порядку 2? порядку 3? порядку 4? порядку 5? Відповідь обґрунтувати.
Задача 2. а) Для даного елемента α, заданого в алгебраїчній (показниковій, тригонометричній) формі, мультиплікативної групи коренів п -го степеня з одиниці  , знайти порядок елемента α;
б) указати циклічну підгрупу, породжену α;
в) указати елемент, симетричний до α;
г) знайти індекс підгрупи (α) у групі , знайти порядок елемента α;
б) указати циклічну підгрупу, породжену α;
в) указати елемент, симетричний до α;
г) знайти індекс підгрупи (α) у групі  ;
д) обчислити порядок елемента α2 у групі. Чи пов’язані якимось співвідношенням порядки елементів α та α2?;
е) зобразити елементи групи (α) на комплексній площині.
Задача 3. Перевірити, чи утворює множина М кільце; кільце з одиницею; комутативне кільце.
Задача 4. Для даного кільця К перевірити, чи є множина М підкільцем, ідеалом кільця К (якщо усі елементи взяті із числового поля Q).
Задача 5а-б). Дано кільце Z цілих чисел. Побудувати перетин, суму, добуток, об’єднання ідеалів. Зробити висновки щодо операцій над ідеалами. ;
д) обчислити порядок елемента α2 у групі. Чи пов’язані якимось співвідношенням порядки елементів α та α2?;
е) зобразити елементи групи (α) на комплексній площині.
Задача 3. Перевірити, чи утворює множина М кільце; кільце з одиницею; комутативне кільце.
Задача 4. Для даного кільця К перевірити, чи є множина М підкільцем, ідеалом кільця К (якщо усі елементи взяті із числового поля Q).
Задача 5а-б). Дано кільце Z цілих чисел. Побудувати перетин, суму, добуток, об’єднання ідеалів. Зробити висновки щодо операцій над ідеалами.
| |
| Індивідуальне завдання № 2 (Теорія чисел).
Задача 1. Для даних чисел визначити цілу і дробову частини числа.
Задача 2. Визначити, що буде стояти у знаменнику дробу після його скорочення; скількома нулями закінчується число n!; запишіть канонічний розклад на множники числа.
Задача 3. Обчислити значення: функції Мьобіуса μ (n); π(n); функції Ейлера φ (n), τ (n), σ(n) для чисел; обчислити τ (n) та записати усі дільники чисел.
Задача 4. Перевірити, чи є дані числа простими; указати прості числа на проміжку [ n 1; n 2].
Задача 5. Обчислити двома способами НСД і НСК чисел; знайти лінійне вираження НСД через дані числа.
Задача 6. Перевірити, чи утворює множина ПСЛ за модулем m?
Задача 7. Перевірити, чи утворює множина ЗСЛ за модулем m?
Задача 8. Знайти остачу від ділення a на b ( .)
Задача 9. Знайти: останню цифру числа; дві останні цифри чисел.
Задача 10. Користуючись ознаками подільності, перевірити, чи діляться указані числа на 27, 37; 7, 11, 13; на 4, 25; 8, 125; 16.
Задача 11. Користуючись ознаками подільності знайти значення цифр .)
Задача 9. Знайти: останню цифру числа; дві останні цифри чисел.
Задача 10. Користуючись ознаками подільності, перевірити, чи діляться указані числа на 27, 37; 7, 11, 13; на 4, 25; 8, 125; 16.
Задача 11. Користуючись ознаками подільності знайти значення цифр 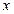 та та
 , які задовольняють вказані умови ( , які задовольняють вказані умови ( .)
Задача 12. Дослідити і розв’язати конгруенції першого степеня з однією невідомою.
Задача 13. Розв’язати невизначені лінійні рівняння в цілих числах.
Задача 14. Визначити довжину періоду і кількість цифр в передперіоді у розкладі в десятковий дріб даного дробу та знайти 2015-ту цифру після коми у розкладі в десятковий дріб даного дробу.
Задача 15. Указати порядок числа а за даним модулем m та розв’язати показникову конгруенцію .)
Задача 12. Дослідити і розв’язати конгруенції першого степеня з однією невідомою.
Задача 13. Розв’язати невизначені лінійні рівняння в цілих числах.
Задача 14. Визначити довжину періоду і кількість цифр в передперіоді у розкладі в десятковий дріб даного дробу та знайти 2015-ту цифру після коми у розкладі в десятковий дріб даного дробу.
Задача 15. Указати порядок числа а за даним модулем m та розв’язати показникову конгруенцію  ; чи є а первісним коренем за даним модулем m? Скільки є первісних коренів за даним модулем? Знайти один з первісних коренів, записати усі первісні корені у вигляді степенів деякого числа та обчислити шість будь-яких первісних коренів.
[Зб. 10, №№ 1-15, свій варіант]. ; чи є а первісним коренем за даним модулем m? Скільки є первісних коренів за даним модулем? Знайти один з первісних коренів, записати усі первісні корені у вигляді степенів деякого числа та обчислити шість будь-яких первісних коренів.
[Зб. 10, №№ 1-15, свій варіант].
| |
| Індивідуальне завдання № 3.
Задача 1. Обчислити добутки многочленів  і і  ; ;  і і  ; виконати ділення з остачею многочлена ; виконати ділення з остачею многочлена  на на  . Ділення перевірити множенням.
Задача 2. Використовуючи схему Горнера, обчислити значення многочлена . Ділення перевірити множенням.
Задача 2. Використовуючи схему Горнера, обчислити значення многочлена  при при  і при і при  та виконати ділення даного многочлена на та виконати ділення даного многочлена на  , , 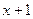 та та  . Що можна сказати про частки і остачі від ділення на . Що можна сказати про частки і остачі від ділення на 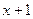 та та  ?
Задача 3 а). Використовуючи схему Горнера, розкласти многочлен ?
Задача 3 а). Використовуючи схему Горнера, розкласти многочлен  за степенями за степенями 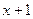 .
Задача 3 б). За схемою Горнера, обчислити значення многочлена .
Задача 3 б). За схемою Горнера, обчислити значення многочлена  і його похідних при і його похідних при  .
Задача 3 в). За схемою Горнера, розкласти многочлен .
Задача 3 в). За схемою Горнера, розкласти многочлен  за степенями за степенями  . Виконати перевірку, розклавши многочлен з отриманої відповіді за степенями . Виконати перевірку, розклавши многочлен з отриманої відповіді за степенями  .
Задача 3 г). Використовуючи схему Горнера, обчислити .
Задача 3 г). Використовуючи схему Горнера, обчислити  .
Задача 4 а). Використовуючи схему Горнера, перевірити, коренем якої кратності є .
Задача 4 а). Використовуючи схему Горнера, перевірити, коренем якої кратності є  і і  для многочлена для многочлена  .
Задача 4 б). Використовуючи результати пункту а), розв’язати рівняння .
Задача 4 б). Використовуючи результати пункту а), розв’язати рівняння  .
Задача 5. Знайти кратні множники многочлена .
Задача 5. Знайти кратні множники многочлена  , використовуючи алгоритм відокремлення кратних множників.
Задача 6 а). Обчислити найбільший спільний дільник і найменше спільне кратне даних многочленів. Виконати перевірку: частки від ділення НСК на , використовуючи алгоритм відокремлення кратних множників.
Задача 6 а). Обчислити найбільший спільний дільник і найменше спільне кратне даних многочленів. Виконати перевірку: частки від ділення НСК на  і і  є взаємно простими (знайти для них НСД і показати, що він є одиницею).
Задача 6 б). Виразити найбільший спільний дільник через многочлени є взаємно простими (знайти для них НСД і показати, що він є одиницею).
Задача 6 б). Виразити найбільший спільний дільник через многочлени  і і  . Виконати перевірку.
Задача 7. Скласти ряд Штурма та відділити дійсні корені многочлена . Виконати перевірку.
Задача 7. Скласти ряд Штурма та відділити дійсні корені многочлена  . Виконати перевірку, побудувавши схематично графік функції з побудовою точок екстремуму або відділивши корені графічно.
Задача 8. Використовуючи метод Феррарі, розв’язати рівняння . Виконати перевірку, побудувавши схематично графік функції з побудовою точок екстремуму або відділивши корені графічно.
Задача 8. Використовуючи метод Феррарі, розв’язати рівняння  четвертого степеня.
Задача 9 а)–б). Знайти раціональні корені многочлена четвертого степеня.
Задача 9 а)–б). Знайти раціональні корені многочлена  , указати їх кратність.
Задача 10. Розкласти многочлени із завдань 4, 5, 8, 9 а-б) на незвідні множники над кільцем , указати їх кратність.
Задача 10. Розкласти многочлени із завдань 4, 5, 8, 9 а-б) на незвідні множники над кільцем  , полями , полями 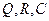 . Що є полем розкладу даних многочленів? Відповідь обґрунтувати.
Задача 11а) Використовуючи теорему Вієта, знайти (не розв’язуючи рівняння) суму квадратів коренів многочлена . Що є полем розкладу даних многочленів? Відповідь обґрунтувати.
Задача 11а) Використовуючи теорему Вієта, знайти (не розв’язуючи рівняння) суму квадратів коренів многочлена  .
Задача 11б) Розв’язати рівняння для усіх значень параметра .
Задача 11б) Розв’язати рівняння для усіх значень параметра  так, щоб один з коренів рівняння так, щоб один з коренів рівняння  дорівнював подвоєному іншому кореню.
Задача 11в) Ребра прямокутного паралелепіпеда є коренями многочлена дорівнював подвоєному іншому кореню.
Задача 11в) Ребра прямокутного паралелепіпеда є коренями многочлена  . Використовуючи теорему Вієта, обчислити об’єм паралелепіпеда, площу його поверхні та діагональ паралелепіпеда.
Свій варіант. . Використовуючи теорему Вієта, обчислити об’єм паралелепіпеда, площу його поверхні та діагональ паралелепіпеда.
Свій варіант.
|
Методи навчання
На основі джерел інформації: словесний, практичний і наочний.
на основі самостійної пізнавальної діяльності: пояснювально-ілюстративний, репродуктивний, частково-пошуковий, дослідницький та проблемний методи навчання.
Методи контролю
Оцінювання активності і знань студентів (індивідуальне опитування) під час практичних занять, поточне тестування за кожний модуль (змістовий модуль), оцінювання за ІДЗ та його захист, бліц-опитування, математичні диктанти, оцінювання класних контрольних робіт, оцінювання теоретичних знань студентів (колоквіуми).
Математичні диктанти складаються з 5 питань типу: дати означення, записати властивості, записати формулу, сформулювати теорему, проілюструвати на прикладі якийсь теоретичний факт. Критерії оцінювання: кожне питання оцінюється 1 пунктом, причому за правильну відповідь студент отримує 1 пункт, відповідь з недоліками –  пункту, відповідь з грубими помилками пункту, відповідь з грубими помилками  пункту, неправильна відповідь 0 пунктів. Студент набирає 5 балів, якщо набрано 4 пункту, неправильна відповідь 0 пунктів. Студент набирає 5 балів, якщо набрано 4  –5 пунктів; 4 бали, якщо набрано 3 –5 пунктів; 4 бали, якщо набрано 3  –4 –4  пунктів; 3 бали, якщо набрано 2 пунктів; 3 бали, якщо набрано 2  –3 –3  пунктів; 2 бали, якщо набрано 1 пунктів; 2 бали, якщо набрано 1  –2 –2  пунктів; 1 бал, якщо набрано 1–1 пунктів; 1 бал, якщо набрано 1–1  пунктів; 0 балів, якщо набрано 0 – пунктів; 0 балів, якщо набрано 0 –  пунктів. пунктів.
Під час практичного заняття (індивідуальне опитування) 5 балів студент отримує за умов правильного застосування теоретичних знань до розв’язування задачі і повної відповіді на теоретичні питання; 4 бали отримує за умови допущення неточностей під час розв’язування задачі (відповіді на теоретичні питання) чи її аргументації; 3 бали отримує за умови допущення неточностей під час розв’язування задачі (відповіді на теоретичні питання) та її аргументації; 2 бали отримує за умови допущення помилок під час розв’язування задачі, відсутності відповіді на теоретичні питання при її аргументації; 1 бал отримує за знання алгоритму розв’язання задачі та розв’язання з грубими помилками; 0 балів за незнання алгоритму розв’язання задачі та теоретичної бази для її розв’язання.
12. Розподіл балів, які отримують студенти
Для заліку (ІІІ семестр)
| Поточне тестування та самостійна робота
| Сума
| | | Практичний модуль
| Підсумкова МКР
| Колоквіум
| ІДЗ 1.1,1.2
| Відвідуваність занять
| | |
| | |
|
|
| 15 + 20
|
| |
За практичний модуль можна набрати 0–25 балів (середня оцінка, помножена на п’ять), максимум 25 балів; МКР – максимум 10 балів; за колоквіум 25 балів, за ІДЗ та захист – максимум 15+20 балів. За відвідуваність занять – максимум 5 балів (64-68 год. – 5 балів; 58-62 год. – 4 бали; 52-56 год. – 3 бали; 46-50 год. – 2 бали; 42-44 год. – 1 бал; менше 40 год. – 0 балів). Усього – максимум 100 балів.
Для екзамену (ІV семестр)
| Поточне тестування та самостійна робота
| Екзамен
| Сума
| | І сем.
| Теорія чисел
| Теорія многочленів
| ІІ сем.
| | К 1
ІДЗ 1
| ІДЗ 2
| К 2
| Практ. модуль
| ІДЗ 3
| МКР
| Практ. модуль
| Відвідуваність занять
| Перевірка ІДЗ
| Максимум
| Максимум
| |
|
|
|
|
|
|
|
| 5*
|
|
|
|


 до канонічного вигляду, знайти ранг і індекс КФ. Чи є КФ додатньо визначеною? Указати тип поверхні другого порядку
до канонічного вигляду, знайти ранг і індекс КФ. Чи є КФ додатньо визначеною? Указати тип поверхні другого порядку  .
Задача 3. Використовуючи метод ортогональних перетворень, звести КФ
.
Задача 3. Використовуючи метод ортогональних перетворень, звести КФ  .
[Зб. 11, №№ 26-28]
.
[Зб. 11, №№ 26-28]
 , знайти порядок елемента α;
б) указати циклічну підгрупу, породжену α;
в) указати елемент, симетричний до α;
г) знайти індекс підгрупи (α) у групі
, знайти порядок елемента α;
б) указати циклічну підгрупу, породжену α;
в) указати елемент, симетричний до α;
г) знайти індекс підгрупи (α) у групі  .)
Задача 9. Знайти: останню цифру числа; дві останні цифри чисел.
Задача 10. Користуючись ознаками подільності, перевірити, чи діляться указані числа на 27, 37; 7, 11, 13; на 4, 25; 8, 125; 16.
Задача 11. Користуючись ознаками подільності знайти значення цифр
.)
Задача 9. Знайти: останню цифру числа; дві останні цифри чисел.
Задача 10. Користуючись ознаками подільності, перевірити, чи діляться указані числа на 27, 37; 7, 11, 13; на 4, 25; 8, 125; 16.
Задача 11. Користуючись ознаками подільності знайти значення цифр 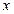 та
та
 , які задовольняють вказані умови (
, які задовольняють вказані умови ( .)
Задача 12. Дослідити і розв’язати конгруенції першого степеня з однією невідомою.
Задача 13. Розв’язати невизначені лінійні рівняння в цілих числах.
Задача 14. Визначити довжину періоду і кількість цифр в передперіоді у розкладі в десятковий дріб даного дробу та знайти 2015-ту цифру після коми у розкладі в десятковий дріб даного дробу.
Задача 15. Указати порядок числа а за даним модулем m та розв’язати показникову конгруенцію
.)
Задача 12. Дослідити і розв’язати конгруенції першого степеня з однією невідомою.
Задача 13. Розв’язати невизначені лінійні рівняння в цілих числах.
Задача 14. Визначити довжину періоду і кількість цифр в передперіоді у розкладі в десятковий дріб даного дробу та знайти 2015-ту цифру після коми у розкладі в десятковий дріб даного дробу.
Задача 15. Указати порядок числа а за даним модулем m та розв’язати показникову конгруенцію  ; чи є а первісним коренем за даним модулем m? Скільки є первісних коренів за даним модулем? Знайти один з первісних коренів, записати усі первісні корені у вигляді степенів деякого числа та обчислити шість будь-яких первісних коренів.
[Зб. 10, №№ 1-15, свій варіант].
; чи є а первісним коренем за даним модулем m? Скільки є первісних коренів за даним модулем? Знайти один з первісних коренів, записати усі первісні корені у вигляді степенів деякого числа та обчислити шість будь-яких первісних коренів.
[Зб. 10, №№ 1-15, свій варіант].
 і
і  ;
;  ; виконати ділення з остачею многочлена
; виконати ділення з остачею многочлена  і при
і при  та виконати ділення даного многочлена на
та виконати ділення даного многочлена на  ,
, 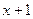 та
та  . Що можна сказати про частки і остачі від ділення на
. Що можна сказати про частки і остачі від ділення на  за степенями
за степенями  . Виконати перевірку, розклавши многочлен з отриманої відповіді за степенями
. Виконати перевірку, розклавши многочлен з отриманої відповіді за степенями  .
Задача 3 г). Використовуючи схему Горнера, обчислити
.
Задача 3 г). Використовуючи схему Горнера, обчислити  .
Задача 4 а). Використовуючи схему Горнера, перевірити, коренем якої кратності є
.
Задача 4 а). Використовуючи схему Горнера, перевірити, коренем якої кратності є  .
Задача 5. Знайти кратні множники многочлена
.
Задача 5. Знайти кратні множники многочлена  , полями
, полями 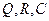 . Що є полем розкладу даних многочленів? Відповідь обґрунтувати.
Задача 11а) Використовуючи теорему Вієта, знайти (не розв’язуючи рівняння) суму квадратів коренів многочлена
. Що є полем розкладу даних многочленів? Відповідь обґрунтувати.
Задача 11а) Використовуючи теорему Вієта, знайти (не розв’язуючи рівняння) суму квадратів коренів многочлена  так, щоб один з коренів рівняння
так, щоб один з коренів рівняння  . Використовуючи теорему Вієта, обчислити об’єм паралелепіпеда, площу його поверхні та діагональ паралелепіпеда.
Свій варіант.
. Використовуючи теорему Вієта, обчислити об’єм паралелепіпеда, площу його поверхні та діагональ паралелепіпеда.
Свій варіант.
 пункту, відповідь з грубими помилками
пункту, відповідь з грубими помилками  пункту, неправильна відповідь 0 пунктів. Студент набирає 5 балів, якщо набрано 4
пункту, неправильна відповідь 0 пунктів. Студент набирає 5 балів, якщо набрано 4 


