
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Структуры различных мерностей с основанием три.Содержание книги
Поиск на нашем сайте
Структура, в основании которой лежит число три, имеет три опорные точки в двухмерном пространстве и является равносторонним треугольником:
| 3 | 2 = 3
Для получения трехмерной структуры необходимо спроецировать двухмерную структуру (треугольник) по всем ее сторонам:
Что бы получить четырехмерную структуру необходимо заставить трехмерную структуру вращаться во времени, т.е. осуществить ее проекцию во времени:
| 3 | 4 = 5
Получение пятимерной структуры осуществляется через проекцию четырехмерной в пространстве (для удобства восприятия углы обозначены цифрами):
       | 3 | 5 = 9 (точка №1 является общей для обоих проекций) | 3 | 5 = 9 (точка №1 является общей для обоих проекций)
Получение структур в следующих по мерности пространств достигается путем проекции структур предыдущих мерностей через общие точки, например - шестимерная структура.
Для получения семимерной структуры необходимо к шестимерной «прицепить» точно такую же шестимерную структуру так, что бы между ними были четыре общие точки:
Умножения в триадной системе.
Как уже известно, существуют три вида умножений:
1) умножение НА (плоскостное, двухмерное) - – 2) умножение ЖДЫ (трехмерное, объемное) - Î 3) умножение Ю (объемно – временное) - *
Для последнего – умножения Ю существует правило: При объемно-временном умножении (Ю) фигура имеет столько опорных точек, сколько изначальных структур соответствовало трехмерной фигуре и ее опорным точкам. Например: Трехмерная фигура (в основании которой треугольник) имеет четыре опорные точки, соответственно объемно-временная фигура будет иметь четыре треугольника соединенных между собой в общей сходящейся точке, т.е. получается пирамида:
| 3 | ов = 5 ов – объемно-временное ограничение
Примеры умножений с основанием три:
Правила вычислений в х’Арийской арифметике.
Существует общий вид умножений в х’Арийской арифметике:
| a | n – | b | m, где: а – структура, подразумевающая количество опорных точек; n – мерность пространства; b – количество повторений в пространстве; m – степень повторений.
В х’Арийской арифметике существует правила для вычислений с несколькими действиями: Все действия выполняются последовательно (независимо от приоритетности операций), особенно: при временных и космонавигаторских вычислениях. При переходах из одной системы мерности в другую, если при очередной операции стоит знак «+» (сложение), то левый актив суммируется до одной цифры, например: 38 + 7 = (3 + 8) + 7 = 11 + 7 = (1 + 1) + 7 = 2 + 7 = 9
Пример:
| 2 | 3 Î | 3 | 3 - | 4 | 2 – | 9 | 3 + 444 + 6
Порядок вычисления:
1. Производим цифровую развертку, т.е. необходимо все привести в обычную арифметическую форму. В данном случае используется общий вид умножений х’Арийской арифметики - | a | n – | b | m :
| 2 | 3 Î | 3 | 3 ≡ 8 – 27 т.к. трехмерная фигура с основанием два будет иметь восемь опорных точек, а | 3 | 3 указывает на три повторения в третьей степени. Знак ЖДЫ, при цифровой развертке, меняется на знак НА, т.к. он являлся в первичной записи выражения указателем на трехмерную структуру. | 4 | 2 – | 9 | 3 ≡ 4 – 729 число четыре в двухмерном пространстве является тем же числом четыре, а | 9 | 3 = 729.
После цифровой развертки арифметическое выражение преобразуется в следующий вид: 8 – 27 - 4 – 729 + 444 + 6
2. Соблюдая правила последовательности выполнения арифметических операций и суммирования левого актива при сложении (т.к. изначально в выражении использовалась разная мерность) приводим выражение к искомому результату:
8 – 27 - 4 – 729 + 444 + 6 ≡ 216 - 4 – 729 + 444 + 6 ≡ 212 – 729 + 444 + 6 ≡ 154548 + 444 + 6 ≡ (1+5+4+5+4+8) + 444 + 6 ≡ 9 + 444 + 6 ≡ 453 + 6 ≡ (4+5+3) + 6 ≡ 3 + 6 ≡ 9 Х’Арийские таблицы умножения Гармоничная система умножения
Триадная система умножения.
Триадная система умножения при вычислении использует структуры малой и трехмерной триад:
- малая триада (основание - 3)
-
Двухмерное триадное умножение.
Малая триада при данном умножении указывает на структуру, построение формы которой используется при вычислении. При двухмерных триадных вычислениях, в качестве первого множителя, используется знак двухмерной триады - Zили z. Второй множитель указывает на количество рядов в триаде. Результатом же является количество точек в получившейся триаде.


Z * 6 \ Z6 = 21
Z * 8 \ Z8 = 32 Z * 9 \ Z9 = 41 Z * 10 \ Z10 = 51 Z * 11 \ Z11 = 66 Z * 12 \ Z12 = 78 Z * 13 \ Z13 = 91 Z * 14 \ Z14 = 105 Z * 15 \ Z15 = 120 Z * 16 \ Z16 = 136
Трехмерное триадное умножение.
При трехмерных триадных вычислениях, в качестве первого множителя, используется знак объемной триады - eили знак z, если задано трехмерное умножение знаком ЖДЫ (&). Второй множитель указывает на количество рядов в триаде. Результатом является количество точек в получившейся триаде.
  z & 3 \ e2 = 10 z & 3 \ e2 = 10
en ≡ en-1 + Zn
Дело в том, что трехмерная триада состоит из соединенных между собой плоскостями малыми триадами, у которых длины сторон увеличиваются на единицу по порядку возрастания номеров рядов в трехмерной триаде (если рядом номер один считать самый верхний ряд). Например структура трехмерной триады сформированная умножением триадно жды три (e3 ) состоит из следующих малых триад:
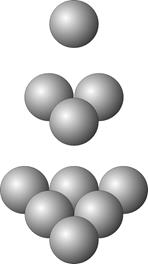
Ряд №1 = 1
Ряд №2 - Z2 = 3
Ряд №3 - Z3 = 6
Триадно жды четыре получается путем «добавления снизу» еще одной малой триады, длина стороны которой будет уже равна четырем, т.е.:
Если при вычислении таблиц трехмерного триадного умножения не брать в расчет таблицы двухмерного умножения, то путем нехитрых вычислений можно получить еще одну формулу:
en ≡ en-1 - en-2 + en-1 + n
Например:
e5 ≡ e5-1 - e5-2 + e5-1 + 5 = e4 - e3 + e4 + 5 = 20 – 10 + 20 + 5 = 35
Ровная система умножения
Данная система так называется от понятия «Ровна» т.е. равномерная структура, где количество точек по любым направлениям равны между собой. Существуют следующие виды Ровны: 1)
 Малая Ровна Малая Ровна
2)
 Трехмерная Ровна Трехмерная Ровна
Умножение Малой Ровны
Результат данного умножения определяется суммой точек в малой Ровне, причем второй множитель показывает количество рядов точек в обеих сторонах Ровны.
 y * 2 \ Y 2 = 4 y * 2 \ Y 2 = 4
y * 4 \ Y 4 = 16
Явно видно, что результат умножения «ровно на …» получается путем плоскостного умножения второго множителя на самого себя, т.е.:
Yn \ n * n
Умножение Трехмерной Ровны
 y & 2 \ E2 = 8 y & 2 \ E2 = 8
 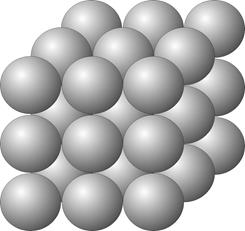 y & 3 \ E3 = 27 y & 3 \ E3 = 27
y & 4 \ E4 = 64
Результат умножения «ровно ЖДЫ …» получается путем плоскостного умножения второго множителя на самого себя со степенью повторений умножения равного самому себе, т.е.:
или, говоря языком «стандартной математики», результат возведения в куб (n3) множителя ровно жды и будет результатом данного умножения.
Пример решения арифметического действия:
т.к. после ровно жды не указан какой-либо множитель, то подразумевается изначальная структура Трехмерной Ровны т.е. E2.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 312; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.01 с.) |




 Данная структура имеет уже четыре опорные точки, т.е.:
Данная структура имеет уже четыре опорные точки, т.е.:
 | 3 | 3 = 4
| 3 | 3 = 4



 Как видно получившаяся фигура имеет пять опорных точек, следовательно:
Как видно получившаяся фигура имеет пять опорных точек, следовательно:










 | 3 | 6 ≡ | 3 | 5 | 3 | 5 - 2 (общие точки) ≡ 16
| 3 | 6 ≡ | 3 | 5 | 3 | 5 - 2 (общие точки) ≡ 16





 | 3 | 7 ≡ | 3 | 6 | 3 | 6 ≡ 16 + 16 – 4 (общ.точки) ≡ 28
| 3 | 7 ≡ | 3 | 6 | 3 | 6 ≡ 16 + 16 – 4 (общ.точки) ≡ 28




 трехмерная триада (основание - 4)
трехмерная триада (основание - 4)




 Z * 2 \ Z2 = 3
Z * 2 \ Z2 = 3





 Z * 3 \ Z3 = 6
Z * 3 \ Z3 = 6
 Z * 7 \ Z7 = 28
Z * 7 \ Z7 = 28


 z & 2 \ e2 = 4
z & 2 \ e2 = 4




 В трехмерных триадных умножениях существует формула, по которой можно вычислить значение любого умножения, зная результат предыдущего вычисления:
В трехмерных триадных умножениях существует формула, по которой можно вычислить значение любого умножения, зная результат предыдущего вычисления:

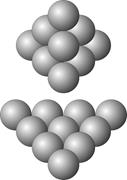














 Результат этого умножения определяется суммой точек в трехмерной Ровне. Второй множитель показывает количество рядов точек во всех трех сторонах Ровны.
Результат этого умножения определяется суммой точек в трехмерной Ровне. Второй множитель показывает количество рядов точек во всех трех сторонах Ровны.





 En \ n * |n|n
En \ n * |n|n

 Y * 3 + E = 9 + E = 9 + 8 = 17
Y * 3 + E = 9 + E = 9 + 8 = 17


