
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка напряжения при сжатии с изгибомСодержание книги
Поиск на нашем сайте
Изгибающий момент, действующий в биссектрисном сечении находится на расстоянии от расчётной оси, равном:
Расчетные сопротивления древесины сосны II сорта: сжатию и изгибу:
растяжению:
Здесь 15 МПа и 9 МПа – значения соответствующих расчетных сопротивлений, принимаемые по СП 64.13330.2011. Радиус инерции сечения:
При расчетной длине полурамы
Для элементов переменного по высоте сечения коэффициент j, учитывающий продольный изгиб, дополнительно умножаем на коэффициент
где b - отношение высоты сечения опоры к максимальной высоте сечения гнутой части:
Коэффициент j определяем по формуле:
где Произведение Определяем коэффициент x, учитывающий дополнительный момент от продольной силы вследствие прогиба элемента, по формуле:
где Изгибающий момент по деформированной схеме:
Для криволинейного участка при отношении
Расчётный момент сопротивления с учетом влияния кривизны: для внутренней кромки:
для наружной кромки:
Напряжение по сжатой внутренней кромке определим по формуле:
Условие прочности по сжатию выполняется.
Недонапряжение составляет:
Условие прочности по растяжению выполняется.
Проверка устойчивости плоской формы деформирования рамы Рама закреплена из плоскости: - в покрытии по наружной кромке прогонами по ригелю; - по наружной кромке стойки стеновыми панелями. Внутренняя кромка рамы не закреплена. Точку перегиба моментов, т.е. координаты точки с нулевым моментом находим из уравнения моментов, приравнивая его к нулю:
Расчетная длинна рамы имеет 2 участка Первый участок: Второй участок: Таким образом, проверку устойчивости плоской фермы деформирования производим для 2-х участков. Проверка устойчивости производится по формуле:
деформирования (в нашем случае n = 2, т.к. на данном участке нет закреплений растянутой зоны);
1) Для сжатого участка
Найдем значение коэффициента
Находим максимальный момент и соответствующую продольную силу на расчетной длине
Максимальный момент будет в сечении с координатами:
Момент по деформируемой схеме:
тогда Так как Коэффициент тогда,
Подставим При расчете элементов переменного по высоте сечения, не имеющих закреплений из плоскости по растянутой кромке или при числе закреплений
Тогда
Подставим значения в формулу:
и получим:
2) Производим проверку устойчивости плоскости формы деформирования растянутой зоны на расчетной длине Гибкость:
Коэффициент
Коэффициент
При закреплении растянутой кромки рамы из плоскости, коэффициент Поскольку верхняя кромка рамы раскреплена прогонами и число закреплений величину
Тогда расчетные значения коэффициентов
Подставляя эти значения в исходную формулу проверки устойчивости плоской формы деформирования, получим:
Конструкции и расчет узлов Опорный узел Определим усилия, действующие в узле: продольная сила:
поперечная сила:
Опорная площадь колонны:
При этом, напряжение смятия
где Нижняя часть колонны вставляется в стальной сварной башмак, состоящей из диафрагмы, воспринимающей распор, двух боковых пластин, воспринимающих поперечную силу, и стальной плиты – подошвы башмака.
При передаче распора на башмак колонна испытывает сжатие поперек волокон, значение расчетного сопротивления которого определяется по СП 64.13330.2011 и для принятого сорта древесины составляет:
Требуемая высота диафрагмы определяется из условия прочности колонны.
Принимаем конструктивно высоту диафрагмы Рассчитываем опорную вертикальную диафрагму, воспринимающую распор, на изгиб как балку, частично защемленную на опорах, с учетом пластического перераспределения моментов:
Найдем требуемый из условия прочности момент сопротивления сечения. При этом примем, что для устройства башмака применяется сталь с расчетным сопротивлением
Тогда толщина диафрагмы:
Принимаем толщину диафрагмы Предварительно принимаем следующие размеры опорной плиты: длина опорной плиты:
ширина:
включая зазор «с» между боковыми пластинами и рамой по 0,5 см. Для крепления башмака к фундаменту принимаем анкерные болты диаметром 20 мм, имеющие следующие геометрические характеристики:
Анкерные болты работают на срез от действия распора. Определяем срезывающее усилие:
Напряжение среза определим по формуле:
Условие прочности анкерных болтов выполняется. Коньковый узел Коньковый узел устраивается путем соединения двух полурам нагельным соединением с помощью накладок. Максимальная поперечная сила в коньковом узле возникает при несимметричной временной снеговой равномерно-распределенной нагрузке на половине пролета, которая воспринимается парными накладками на болтах. Поперечная сила в коньковом узле при несимметричной снеговой нагрузке:
где Определяем усилия, на болты, присоединяющие накладки к поясу.
где
По правилам расстановки нагелей отношение между этими расстояниями может быть Принимаем диаметр болтов 16 мм и толщину накладок 75 мм. Несущая способность на один рабочий шов при направлении передаваемого усилия под углом 900 к волокнам находим из условий: Изгиба болта:
но не более где а – толщина накладки (см) d – диаметр болта (см) ka- коэф. зависящий от диаметра болтов и величины угла между направлением усилия и волокнами древесины накладки Смятия крайних элементов-накладок при угле смятия 900:
Смятие среднего элемента – рамы при угле смятия a=900 – 300 = 600
где с – ширина среднего элемента рамы, равная b (см) Минимальная несущая способность одного болта на один рабочий шов: Тmin=4,62 кН Необходимое количество болтов в ближайшем к узлу ряду:
Количество болтов в дальнем от узла ряду:
Принимаем расстояние между болтами по правилам расстановки СП l1 ≥ 7*d = 7*1,6 = 11,2 см, принимаем 12 см, тогда расстояние l2 =3*l1 = 3*12 = 36 см Ширину накладки принимаем ³ 9,5*d, что равно 152 мм, согласно сортамента по ГОСТ 24454-80*(3) принимаем ширину накладки 175 мм, тогда - расстояние от края накладки до болтов S2 ³ 3*d = 3*1,6 =4,8 см, принимаем 5 см; - расстояние между болтами S3 ³ 3,5*d = 3,5*1,6 = 5,6 см, принимаем S3= 175-2*50=75 мм,что больше чем 56 мм Изгибающий момент в накладках равен:
Момент инерции накладки, ослабленной отверстиями диаметром 1,2 см:
Момент сопротивления накладки:
Напряжение в накладках:
где 2 – количество накладок Rи = 13 МПа –расчетное сопротивление древесины изгибу по табл.3 СНиП Следовательно, принимаем 2 болта в первом ряду и 1 болт в крайнем ряду. Проверку боковых накладок на изгиб не выполняем ввиду очевидного запаса прочности. Используемая литература
В.И.Линьков, Е.Т. Серова, А.Ю. Ушаков МГСУ, Москва, 2007г.
|
|||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 289; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.63.208 (0.011 с.) |

 .
.
 .
. .
. , гибкость равна:
, гибкость равна: .
. :
: ,
, .
.
 – коэффициент, принимаемый для деревянных конструкций.
– коэффициент, принимаемый для деревянных конструкций.
 ,
, − усилию в ключевом шарнире.
− усилию в ключевом шарнире. .
. согласно СП 64.13330.2011 прочность проверяем для наружной и внутренней кромок с введением коэффициентов
согласно СП 64.13330.2011 прочность проверяем для наружной и внутренней кромок с введением коэффициентов  и
и  к
к  .
. ;
; .
. ;
; ;
; ;
; ;
; ;
; Принимаем:
Принимаем: 
 ;
; ;
; ;
; ;
; ;
;  .
. .
. .
. , где:
, где: – продольная сила на криволинейном участке рамы;
– продольная сила на криволинейном участке рамы; – изгибаемый момент, определяемый из расчета по деформированной схеме;
– изгибаемый момент, определяемый из расчета по деформированной схеме; – коэффициент продольного изгиба, определяемый по СП 64.13330.2011;
– коэффициент продольного изгиба, определяемый по СП 64.13330.2011; – коэффициент, учитывающий наличие закреплений растянутой зоны из плоскости
– коэффициент, учитывающий наличие закреплений растянутой зоны из плоскости – коэффициент, определяемый по СП 64.13330.2011.
– коэффициент, определяемый по СП 64.13330.2011. находим максимальную высоту сечения из соотношения:
находим максимальную высоту сечения из соотношения: .
.
 .
.

 – коэффициент, зависящий от формы эпюры изгибающих моментов на участке
– коэффициент, зависящий от формы эпюры изгибающих моментов на участке  определяемый по СП 64.13330.2011 (
определяемый по СП 64.13330.2011 (

 и
и 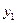 ;
;



 ,
,  ,
, ,
,  .
. , принимаем
, принимаем  , где
, где  .
. для
для  ,
, ,
, ,
, 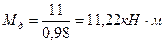 .
. , коэффициенты
, коэффициенты  и
и  в плоскости
в плоскости  :
:
 .
.



 , где имеются закрепления растянутой зоны.
, где имеются закрепления растянутой зоны. ;
; ;
; .
. , а
, а  .
. ,
, следует принимать равной 1, тогда:
следует принимать равной 1, тогда: ;
; , где
, где ;
; .
.

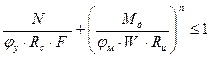
 ,
, ;
; .
. .
. составляет:
составляет: ,
, – расчетное сопротивление смятию, которое определяется по СП 64.13330.2011.
– расчетное сопротивление смятию, которое определяется по СП 64.13330.2011. .
. .
. .
.
 .
. .
. .
. . Боковые пластины принимаем той же толщины в запас прочности.
. Боковые пластины принимаем той же толщины в запас прочности. ,
,
 ;.
;. кН
кН ,
, ,
, – расчетная снеговая нагрузка, вычисленная ранее.
– расчетная снеговая нагрузка, вычисленная ранее.
 ,
, – расстояние между первым рядом болтов в узле;
– расстояние между первым рядом болтов в узле; – расстояние между вторым рядом болтов.
– расстояние между вторым рядом болтов. или
или  . Мы приняли отношение 1/3
. Мы приняли отношение 1/3 кН
кН кН
кН кН
кН кН
кН , принимаем 2 болта
, принимаем 2 болта , принимаем 1 болт
, принимаем 1 болт кНсм
кНсм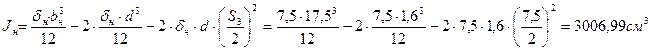
 см3
см3



