
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типовые динамические звенья и их характеристики.Содержание книги
Поиск на нашем сайте
Динамическим звеном называется элемент системы, обладающий определенными динамическими свойствами. Любую систему можно представить в виде ограниченного набора типовых элементарных звеньев, которые могут быть любой природы, конструкции и назначения. Как видно из разложения, можно выделить следующие звенья: 1. Усилительное (безынерционное). 2. Дифференцирующее. 3. Форсирующее звено 1-го порядка. 4. Форсирующее звено 2-го порядка. 5. Интегрирующее. 6. Апериодическое (инерционное). 7. Колебательное. 8. Запаздывающее. Логарифмические частотные характеристики звена (рис. 18) определяются по формуле:
Частотные характеристики звена (рис. 17а-в) определяются соотношениями:
Билет № 9
И малом сигнале. Методы анализа. При большом действующем сигнале. Рассмотрим простую нелинейную цепь.
Составленое на основе законов Ома и Кирхгофа при выбраном базисе. Компонентные уравнения (элементные) Эти уравнения составлены на основе законов Ома. Определим как входное действие и уравнение компонентов.
2. 3. 4. 5.
6.
В (1) подставим уравнение ветвей. Потом вместо напряжения вводим уравнение из (2).
малого сигнала Этот режим являеться частным случаем общего нелинейного динамического режима. Если сигнал малый, то нелинейная функція в области статического режима можна заменить на линейные.
Нелинейные C і L при лионеризации выбирают равным значениям в точке статического режима. Линейная модель, при действии малого сигнала, может бать получена из нелинейных для більшого сигнала путем лионеризации функций в области статического режима. Линейная модель может быть получена на основе линейных эквивалентных схем.
Длинные линии. Режимы работы. Прохождение сигнала. Искажение сигнала в линии. в случае передачи энергии в линии передач, антенны, фидеры, волноводы. Следует учитывать, что электромагнитные поля в этих устройствах распределены по всей их длине и в пространстве. В таких цепях имеем дело с распределёнными индуктивностями, ёмкостями, сопротивлениями. Поэтому они называются цепями с распределёнными параметрами. Ток и напряжение на выходе небольшого участка цепи с распределёнными параметрами не равны току и напряжению на его входе и отличаются как по величине, так и по фазе. Из широкого класса цепей с распределёнными параметрами рассмотрим длинные линии. Они предназначены для передачи энергии на расстояние и чаще всего имеют длину, которая превосходит длину волны. Длинные линии называются однородными, если конструктивные данные остаются неизменными по всей их длине.
Режим бегущей волны характеризуется наличием только падающей волны, распространяющейся от генератора к нагрузке. Отраженная волна отсутствует. Мощность, переносимая падающей волной, полностью выделяется в нагрузке. В этом режиме B U = 0, | Г | = 0, k бв = k св = 1[9]. Режим стоячей волны характеризуется тем, что амплитуда отраженной волны равна амплитуде падающей B U = A U т.е. энергия падающей волны полностью отражается от нагрузки и возвращается обратно в генератор. В этом режиме, | Г | = 1, k св = В режиме смешанных волн амплитуда отраженной волны удовлетворяет условию 0 < B U < A U т.е. часть мощности падающей волны теряется в нагрузке, а остальная часть в виде отраженной волны возвращается обратно в генератор. При этом 0 < | Г | < 1, 1 < k св <
Билет № 10 Модели НРЭУ для динамического режима (частотная область) малого и Большого сигналов. Методы анализа. Режим малого сигнала (частотная область) В данном случае параметры зависят от частоты, тому потому математическая модель может бать получена на основе линейной модели для временной области если воспользоваться заменой:
Воспользовавшись этим получим:
2 способ получения модели основаних на составлении ее по линейной эквивалентной схеме.
|
|||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 292; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.69.226 (0.008 с.) |



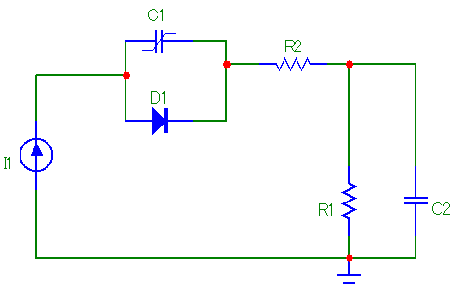 1. Модели НРЭУ для динамического режима во временной области при большом
1. Модели НРЭУ для динамического режима во временной области при большом


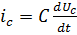





 r R C
r R C















 , k бв = 0[9].
, k бв = 0[9].

 ]
]





