
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операционные усилители (ОУ).Содержание книги
Поиск на нашем сайте
Билет № 1 Операционные усилители (ОУ). Использование ОУ для построения функциональных узлов. Операционные усилители – сложные микросхемы, что включают в себя малошумные широкополосные усилители мощности. Характеристики: - Коэффициент усиления – достаточно большой 106, при этом не возбуждаясь, потому что имеют искривления и широкую полосу пропускания. - Широко используются в ЦАП (полоса пропускания до 2 ГГц). Это дает возможность отказаться от некоторых традиционных элементов. Усилители играют очень важную роль и широко применяются. Кроме обычных, существуют и импульсные усилители, которые являються широкополосными устройствами. В настоящее время ОУ получили широкое применение как в виде отдельных чипов, так и в виде функциональных блоков в составе более сложных интегральных схем. Такая популярность обусловлена тем, что ОУ является универсальным блоком с характеристиками, близкими к идеальным, на основе которого можно построить множество различных электронных узлов. Расчет моoностей методом комплексных амплитуд. Баланс мощностей. Условия согласования. Суть метода заключается в следующем: § Для всех реактивных элементов определяется их комплексный импеданс. § Все токи и напряжения рассматриваются в виде комплексных амплитуд. После введения этих замен задача анализа цепи сводится к задаче анализа цепи на постоянном токе: § импедансы трактуются как обычные сопротивления § комплексные амплитуды токов и напряжений как обычные токи и напряжения Таким образом, мы избавились от реактивности элементов и зависимости от времени сигналов. Эти факторы, затрудняющие математическое описание схемы, теперь перенесены в сигнал: все параметры зависят от частоты гармонического сигнала и являются комплекснозначными. Задача анализа цепи на постоянном токе решается соответствующими методами, например, методом узловых потенциалов или методом контурных токов. После нахождения всех искомых комплексных амплитуд их можно при необходимости перевести обратно в гармонические сигналы.
u(t)=Um*sin(wt); U = Um*ej0= Um; i=Im=sin(wt-j). Потужність: P=Pcp= U= U, I – діючі значення напруги та струму. cosj характеризує втрати. Звичайно cosj Тоді P=(R/ cosj)*I*I*cosj=RI2=U2G. [P]=Вт. Значить середня за період потужність дорівнює потужності, що розсіюється на активному опорі (провідності). Окрім активної потужності, існує і реактивна потужність Q. Q=I2X=U2B. Тоді повна потужність: S =P+jQ=S*ejj, S= S =UI cosj+jUI sinj=UI*ejj= UI*. Значить: P=Re{ UI* }=Re{S}; Q=Im{ UI* }=Im{S}; cosj=P/S – коефіціент потужності. Чим більше cosj, тим менші втрати енергії. При P=S cosj=1, Q=0. Тоді ланцюг буде виключно активним. Умова передачі максимальної потужності в навантаження: Z генер.= Z *ланц. Тобто сума повних комплексних потужносетй в усіх гілках дорівнює нулю. Теорему можна сформулювати і інакше: сума комплексних потужностей, що віддаються незалежними джерелами, дорівнює сумі потужностей, що споживають усі гілки основного ланцюга:
З умови балансу потужностей випливають умови балансу активної та реактивної потужностей:
Билет № 2 Основные понятия и законы электрических цепей. Резистивные цепи. Преобразование цепей. I закон Кірхофа (закон струмів Кірхофа) (формулюється по відношенню до вузлів кола і відображає той факт, що у вузлах не можуть накопичуватись заряди): Алгебраїчна сума струмів віток, які сходяться у будь-якому вузлі електричного кола, дорівнює нулю.
n – число віток у вузлі. II закон напруг Кірхгофа (формулюється відносно контурів): Алгебраїчна сума напруг віток в будь-якому контурі дорівнює нулю.
m – кількість віток в контурі. Закон Ома для R-елементів. Um=R*Im; U(t)=R*i(t). В даному випадку струм буде постійним, тому
U=Um*sin(wt+ju); i=U/R=(Um/R)*sin(wt+ju)=Im*sin(wt+ju)={ju =ji }= Im*sin(wt+ji).
Як бачимо, струм і напруга в резистивних ланцюгах по фазі співпадають. При послідовному або при паралельному з¢єднанні резистивних елементів струм в ланцюзі визначається тими ж співвідношеннями після знаходження еквівалентного опору Re. Перехід від послідовного з’єднання елементів до паралельного. Z=R+jX=1/Y=1/(G-jB)=(G+jB)/ (G2+B2)=G/(G2+B2)+j*B/(G2+B2). Отже: R= G/(G2+B2); X= B/(G2+B2). Аналогічно можна вивести, що: G= R/(R 2+X2); B= X/(R 2+X2).
Билет № 3 Переходные процессы в ЛРЭУ. Билет № 4 Билет № 5 Билет № 6 Билет № 7 II закон напруг Кірхгофа (формулюється відносно контурів): Алгебраїчна сума напруг віток в будь-якому контурі дорівнює нулю.
m – кількість віток в контурі. Напруга, яка співпадає з напрямком обходу контуру, - “+”, а яка не співпадає – “-“. Первый: Алгебраическая сума токов ветвей сходящихся в одном узле цепи =0. Второй: Алгебраическая сума напряжений ветвей в любом контуре цепи =0. Билет № 8 Модели НРЭУ для статистического режима. Методы анализа. Примеры расчета.
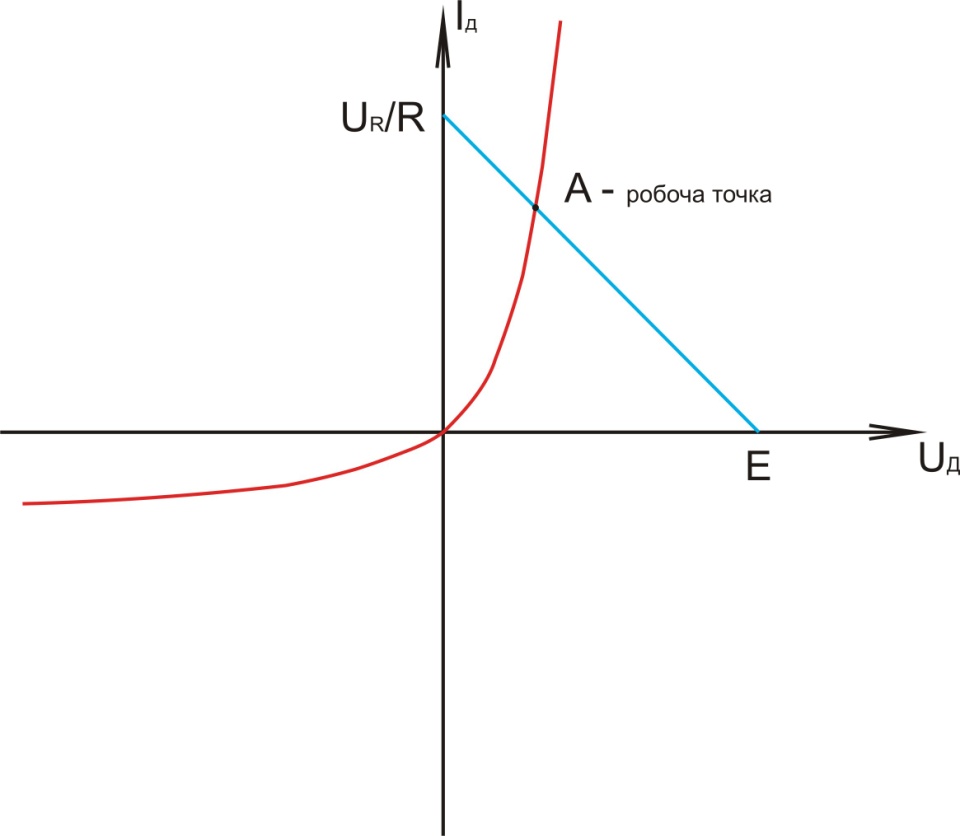
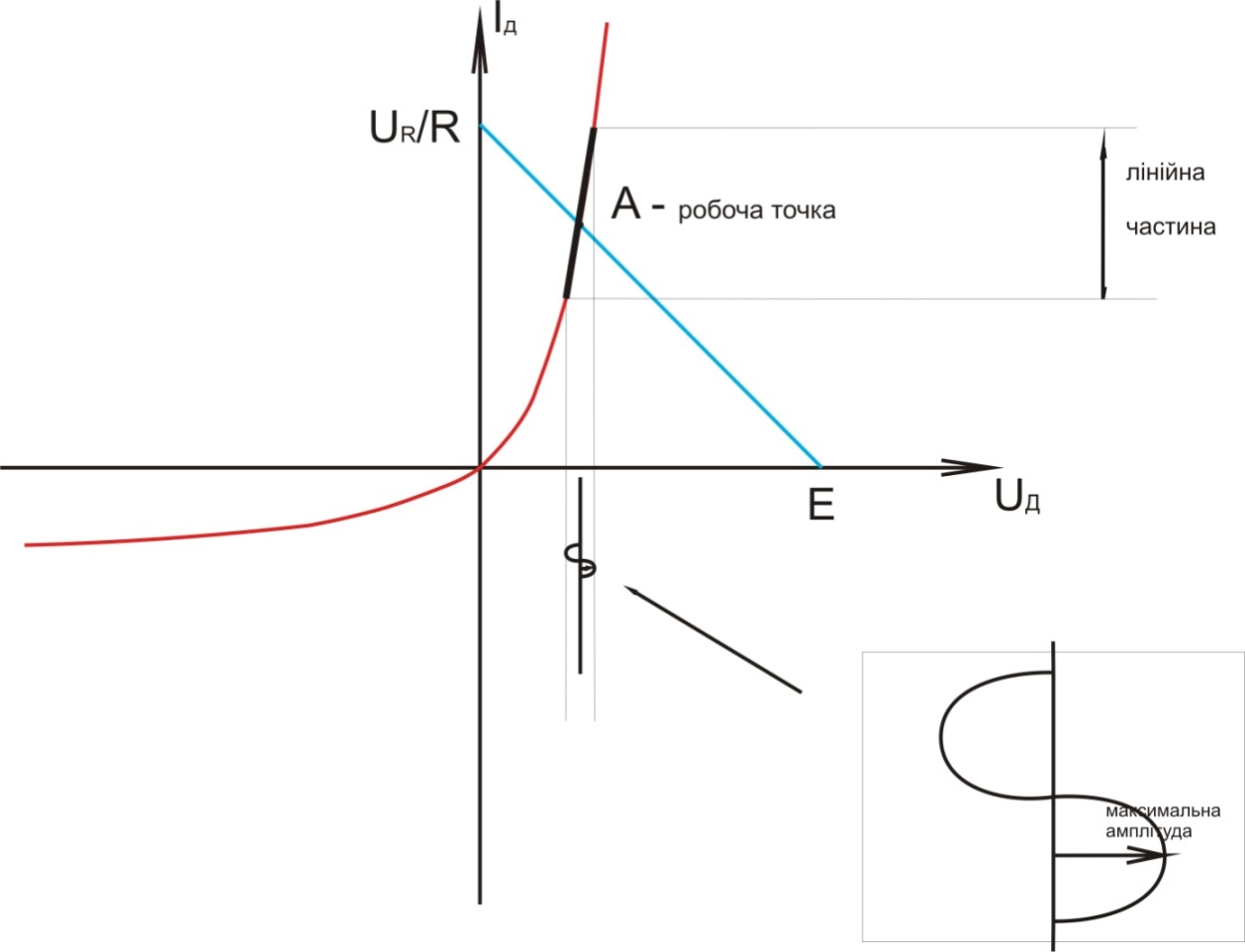
Построим линю нагрузки, для определения рабочей точки:
Найдя рабочую точку, мы выбираем в ее окрестности линейный участок ВАХ для нахождения максимальной амплитуды входного сигнала, при котором можно лионеризовать данную схему. Лионеризация это замена нелинейных элементов схемы на линейные в определенных допустимых границах для упрощения расчетов
Билет № 9
Искажение сигнала в линии. в случае передачи энергии в линии передач, антенны, фидеры, волноводы. Следует учитывать, что электромагнитные поля в этих устройствах распределены по всей их длине и в пространстве. В таких цепях имеем дело с распределёнными индуктивностями, ёмкостями, сопротивлениями. Поэтому они называются цепями с распределёнными параметрами. Ток и напряжение на выходе небольшого участка цепи с распределёнными параметрами не равны току и напряжению на его входе и отличаются как по величине, так и по фазе. Из широкого класса цепей с распределёнными параметрами рассмотрим длинные линии. Они предназначены для передачи энергии на расстояние и чаще всего имеют длину, которая превосходит длину волны. Длинные линии называются однородными, если конструктивные данные остаются неизменными по всей их длине. Режим бегущей волны характеризуется наличием только падающей волны, распространяющейся от генератора к нагрузке. Отраженная волна отсутствует. Мощность, переносимая падающей волной, полностью выделяется в нагрузке. В этом режиме B U = 0, | Г | = 0, k бв = k св = 1[9]. Режим стоячей волны характеризуется тем, что амплитуда отраженной волны равна амплитуде падающей B U = A U т.е. энергия падающей волны полностью отражается от нагрузки и возвращается обратно в генератор. В этом режиме, | Г | = 1, k св = В режиме смешанных волн амплитуда отраженной волны удовлетворяет условию 0 < B U < A U т.е. часть мощности падающей волны теряется в нагрузке, а остальная часть в виде отраженной волны возвращается обратно в генератор. При этом 0 < | Г | < 1, 1 < k св <
Билет № 10 Характеристики. Параметры. Резонансом називається такий стан електричного ланцюга, що складаєтья з різнохарактерних реактивних елементів, при якому фазовий зсув між вхідним струмом та прикладеною напругою дорівнює нулю. Ланцюги, в яких виникає резонанс, називаються резонансними ланцюгами або резонансними коливальними контурами. . Послідовний резонансний контур (резонанс напруг) u(t)= Um *sinwt; Z=R+jX=R+j(wL-1/wC); I=U/Z=U/(R+jX); j=arctg{(wL-1/wC)/R}=arctg(X/R).Умова резонансу: j=0. Значить Х=0, wL-1/wC=0. w=w0= На частоті резонансу Z =R. В цьому випадку струм по фазі співпадає з напругою, а максимальний струм дорівнює: I0=U/R.Опори при резонансі:XL0=w0L;XC0=1/w0C. добротністю контуру:Q=r/R. затуханням контура:d=1/Q. R, L, C – первинні параметри контур, а r, w0, Q, d – вторинні.
Паралельний коливальний контур (резонанс струмів)
Y=Y1+Y2=G1+G2-j(B1-B2)=G-jB; Y1=G1-jB1; Y2=G2+jB2; G1=R1/Z12; B1=wL/Z12; G2=R2/Z22; B1=1/wCZ22; Z1= Умова резонансу: j=arctg B/G=0; B=B1-B2=wL/(R12+(wL)2)-1/(R22+1/(wC)2)=0. wр= wр= В паралельному контурі резонанс можливий при умові, що R1<r, R2<r або R1>r, R2>r. Резонансні струми:Ip1=UB1= Ip2=UB2; Загальний струм: I0=UGp=U/Rp; R0p=
Билет № 11 Цепей. Метод вузлових потенціалів Він базується на законі струмів Кірхгофа та законі Ома. Цей метод дозволяє зменшити число рівнянь до величини Nв-1, де Nв – кількість вузлів. В основі методу вузлових потенціалів лежить розрахунок напруг в Nв-1 вузлах ланцюга відносно базисного вузла. Після цього, на основі закону Ома, знаходять струми або напруги на відповідних гілках. Метод контурних струмів Для зменшення числа необхідних рівнянь та для спрощення розрахунків, окрім метода вузлових потенціалів, використовують і метод контурних струмів. Якщо в першому випадку в якості незалежних змінних використовують вузлові напруги (потенціали), то в другому випадку за незалежні змінні обирають контурні струми. В основі методу контурних струмів лежить введення в кожний контур умовного контурного струму. Струм беруть зі знаком “+”, якщо його напрям співпадає з напрямом обходу контура, і зі знаком “-” – в протилежному випадку. При цьому для методу контурних струмів виконуються перший та другий закони Кірхгофа. Метод контурних струмів дозволяє зменшити кількість рівнянь до числа незалежних контурів. Якщо в схемі контурів менше, ніж вузлів, то кількість рівнянь згідно з методом контурних струмів буде меншою, в порівнянні з методом вузлових потенціалів.
Билет № 12 Билет № 13 А хз что тут написать Характеристики. Параметры.
Билет № 14 Билет № 15 1. Принцип модуляции. Модуляторы и демодуляторы. Схемотехнические решения. Применение. Модуля́ция — процесс изменения одного или нескольких параметров высокочастотного модулируемого колебания по закону информационного низкочастотного сообщения ( сигнала ). В результате спектр управляющего сигнала переносится в область высоких частот, ведь для эффективного вещания в пространство необходимо чтобы все приёмо-передающие устройства работали на разных частотах и «не мешали» друг другу. Это процесс «посадки» информационного колебания на априорно известную несущую. Передаваемая информация заложена в управляющем сигнале. Роль переносчика информации выполняет высокочастотное колебание, называемое несущим. В качестве несущего могут быть использованы колебания различной формы (прямоугольные, треугольные и т. д.), однако чаще всего применяются гармонические колебания. В зависимости от того, какой из параметров несущего колебания изменяется, различают вид модуляции ( амплитудная, частотная, фазовая и др.). Модуляция дискретным сигналом называется цифровой модуляцией или манипуляцией. Общий принцип модуляции состоит в изменении одного или нескольких параметров несущего колебания (переносчика) f(а,b,...,t) в соответствии с передаваемым сообщением. Так, например, если в качестве переносчика выбрано гармоническое колебание Если переносчиком является периодическая последовательность импульсов
2. Алгоритмическое представление методов расчета и применение программ при анализе и расчете ЛРЭУ. радиоэлектронике приходится иметь дело с различными сигналами и разными цепями, при прохождении сигналов по таким цепям возникают переходные процессы, в результате которых форма передаваемого сигнала может измениться. Большинство устройств содержит в себе совокупность линейных и нелинейных элементов, что усложняет строгий анализ прохождения сигналов. Однако имеется достаточно широкий круг задач, которые успешно можно решать линейными методами, даже если в цепи имеется нелинейный элемент. Это относится к устройствам, в которых сигналы настолько малы по амплитуде, что нелинейностью характеристик нелинейного элемента можно прeнебречь, так что его также можно считать линейным.Большинство методов анализа прохождения сигналов через линейную цепь основано на основополагающем принципе - принципе суперпозиции, при котором реакция цепи на сложное воздействие может быть определена как сумма реакций на более простые сигналы, на которые можно разложить сложное воздействие. Реакция линейной цепи на известное простое (тестовое) воздействие называется системной (т.е. зависящей только от цепи) передаточной характеристикой цепи. Сама передаточная характеристика может быть определена: а) классическим методом, при котором цепь описывается системой линейных дифференциальных уравнений, в правой части которой записано тестовое воздействие; этим методом чаще всего определяются реакции на единичную ступенчатую функцию или дельта-функцию, так называемые переходная и импульсная характеристики цепи, являющиеся передаточными характеристиками цепи для метода наложения (или метода интеграла Дюамеля); классическим методом при достаточно несложных цепях б) комплексным методом, если в качестве тестового сигнала используется гармоническое колебание; в этом случае определяется такая передаточная характеристика цепи как частотная характеристика, являющаяся основой частотного метода анализа; в) операторным методом, при котором используется аппарат преобразования Лапласа, в результате чего определяется операторная передаточная характеристика цепи, так как операторный метод использует сигнал вида ept, где p =s + jw, то при замене в операторной передаточной характеристике p на jw получается частотная передаточная характеристика, кроме того, как будет показано ниже, оригинал от операторной передаточной характеристики является импульсной характеристикой цепи.Поэтому можно классифицировать методы анализа прохождения сложных сигналов на а) частотные, применяющиеся главным образом для анализа установившихся процессов;б) временные, использующие переходную или импульсную характеристику цепи, применяющиеся в случаях быстро меняющихся (импульсных) сигналов, когда важными являются переходные процессы в цепи.При анализе прохождения сигналов через узкополосные избирательные цепи эти же методы можно использовать не для мгновенных значений сигнала, а для медленно-меняющейся огибающей.
ЕКЗАМЕНАЦІЙНИЙ БІЛЕТ N 16 1. Переходные процессы в R, L, C - цепях.
а) Методика расчета переходных процессов классическим методом для напряжения на конденсаторе в цепи на рис. 3 можно записать Тогда для первого случая принужденная составляющая этого напряжения Характеристическое уравнение цепи 1. 2. 3. Таким образом, и напряжение на катушке индуктивности
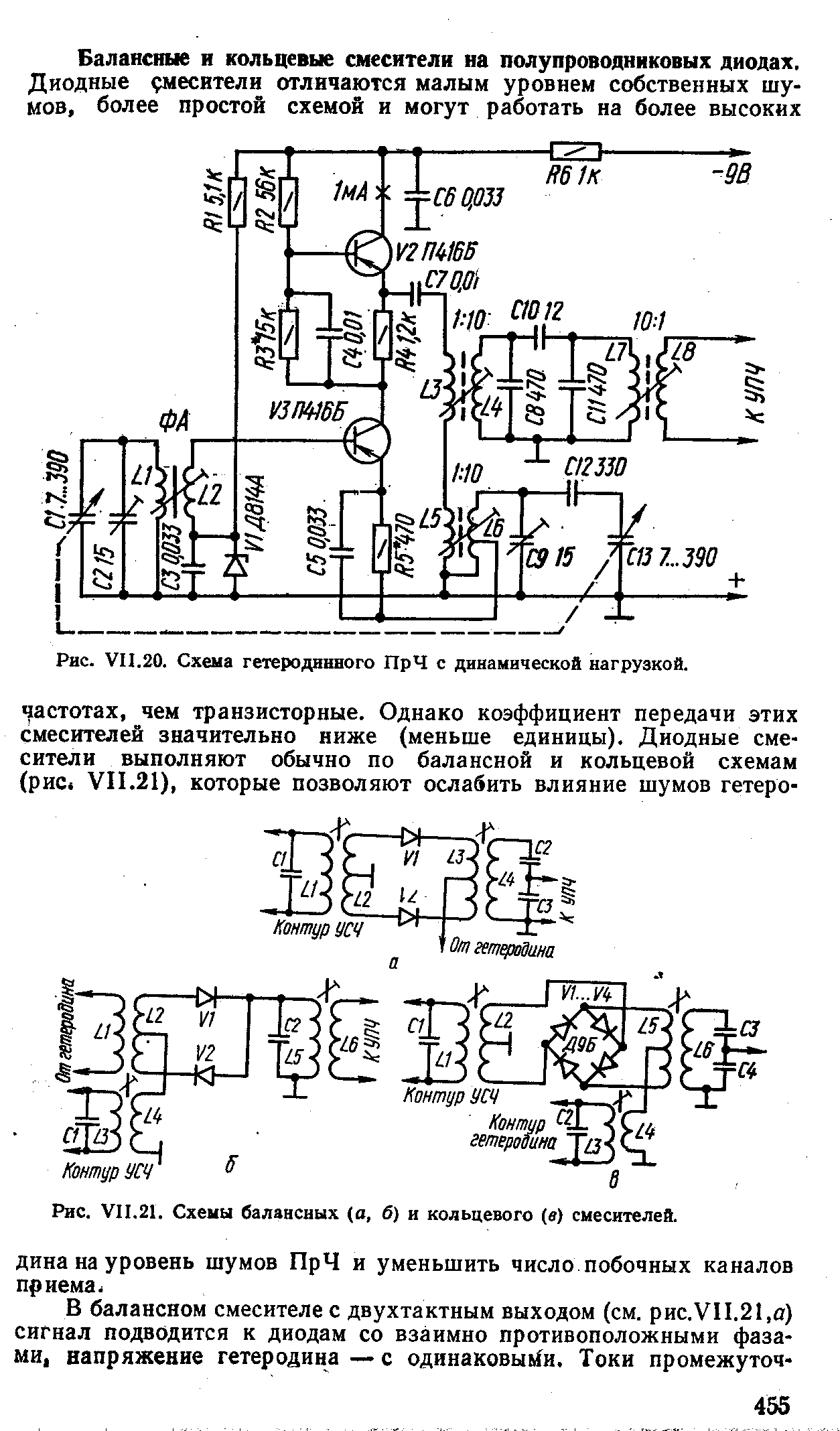
ЕКЗАМЕНАЦІЙНИЙ БІЛЕТ N 17 1. Балансные и кольцевые преобразователи частоты (ПЧ). Алгоритмы проектирования ПЧ.
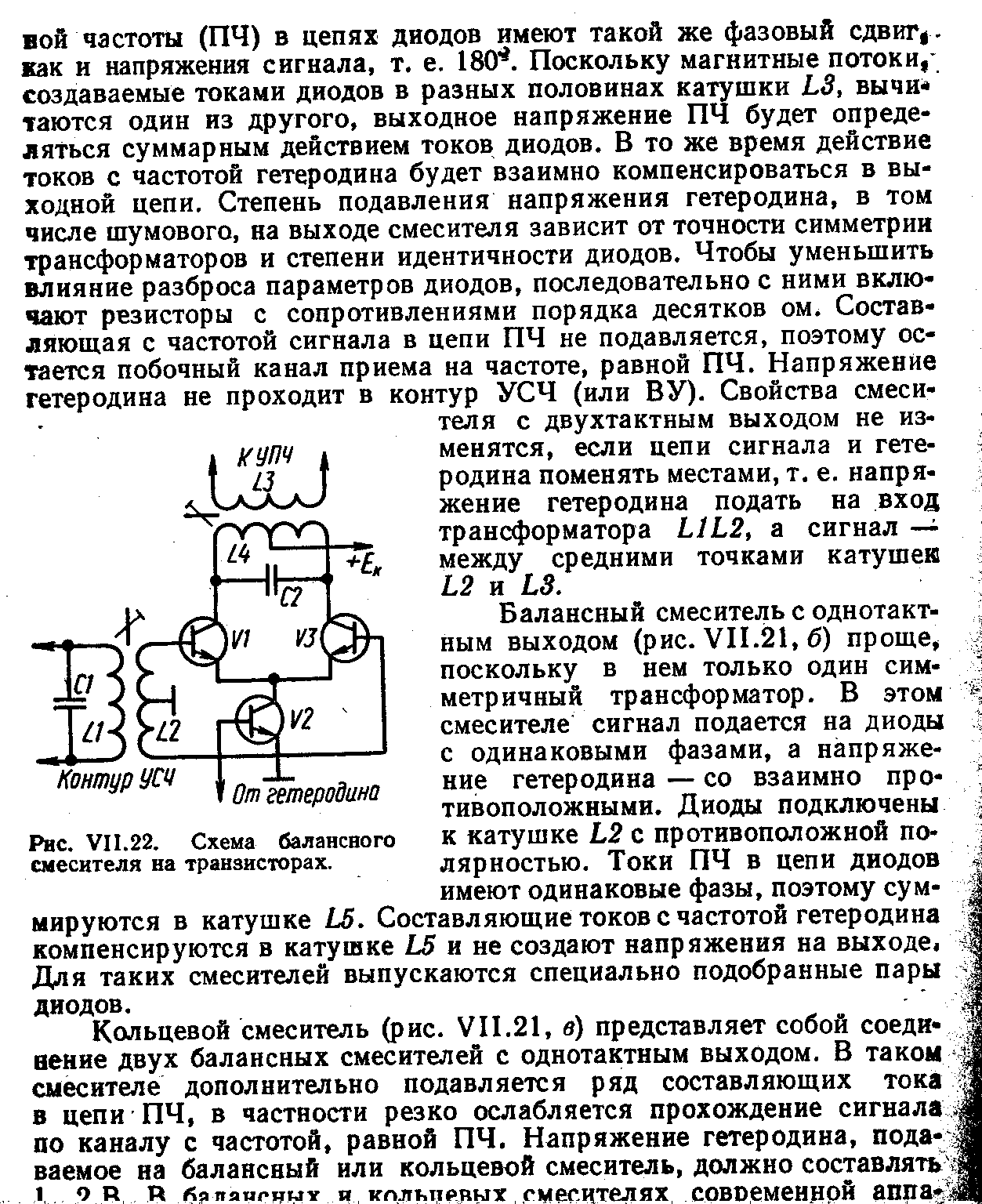
2. Основы теории четырехполюсников. ЕКЗАМЕНАЦІЙНИЙ БІЛЕТ N 18 1. Уравнения четырехполюсников. Первичные, вторичные параметры. Соединения Соединение четырехполюсников, определение параметров соединений Складні чотириполюсники можна представити у вигляді з'єднань простих чотириполюсників. При цьому параметри складного чотириполюсника можуть бути знайдені через параметри простих чотириполюсників, з яких він складається. Каскадне з’днання чотириполюсників.
Так як
Тобто матриця складного чотириполюсника обчислюється за формулою: |A|=|AI*AII|. Це правило поширюється на будь-яку кількість каскадно з’єднаних чотириполюсників. Взагалі, при каскадному з'єднанні чотириполюсників рекомендується використовувати аппарат А-матриць. Послідовне з’єднання чотириполюсників Для послідовного з’єднання рекомендується використовувати Z-матрицю. В цьому випадку напруги на вході і виході дорівнюють відповідно: U1= U1І+ U1ІІ;U2= U2І+ U2ІІ. Матричні рівняння додаються, а результуюча матриця |Z| буде дорівнювати: |Z|=|ZI+ZII|.Результуюча система буде мати вигляд:|U|=|ZI+ZII|*|I|=|Z|*|I|. ЕКЗАМЕНАЦІЙНИЙ БІЛЕТ N 21 1. Символический метод расчета линейных цепей. Пример применения.
2. Обратные связи и их влияние на параметры и характеристики усилителей. Обратной связью называется эффект подачи части выходного напряжения усилителя на его вход. Разработка в 1927 году принципов обратной связи (ОС) позволило резко изменить важнейшие параметры усилителей, поэтому в настоящее время ОС является неотъемлемой частью любого высококачественного усилителя.
подается на вход усилителя, где алгебраически суммируется со входным напряжением. В результате реальное напряжение на входе усилителя составляет величину: Если принять коэффициенты К и Подставляя в данное выражение значение U1 и UОС можно получить: Отсюда коэффициент усиления усилителя, охваченного обратной связью:
ЕКЗАМЕНАЦІЙНИЙ БІЛЕТ N 22 1. Электрические фильтры. Классификация. Свойства. Метод синтеза и проектирования. Схемотехнические решения. Электрический фильтр - это четырехполюсник, пропускающий без ослабления или с малым ослаблением колебания определенных частот и пропускающий с большим ослаблением колебания других частот. Полоса частот, в которой ослабление мало, называется полосой пропускания. Полоса частот, в которой ослабление велико, называется полосой непропускания (задерживания). Между этими полосами находится переходная область.По расположению полосы пропускания на шкале частот различают следующие фильтры: нижних частот (ФНЧ), в которых полоса пропускания располагается на шкале частот от w = 0 до некоторой граничной частоты верхних частот (ФВЧ) с полосой пропускания от частоты Требования к Рабочее ослабление: Квадрат амплитудно-частотной характеристики таких фильтров могут при надлежащем выборе степени полинома (порядка фильтра) и коэффициентов В теории электрических фильтров вместо формул (2.2) и (2.3) используют другие, также универсальные для любого типа фильтра:
Другие типы фильтров могут быть получены из ФНЧ с помощью замены переменной (частоты). Для этого во всех выражениях, содержащих переменную W, нужно произвести замену переменной таким образом, чтобы характеристики ФНЧ перешли в характеристики соответствующего фильтра. Подобная замена переменной W называется преобразованием частоты, а исходный ФНЧ – фильтром НЧ-прототипа. 2. Математические модели и методы анализа НРЭУ во временной области. Математическая модель при воздействии малого сигнала (линейный режим работы) Этот режим является частным случаем общего нелинейного динамического режима. Если сигнал малый, то нелинейная функция в области статического режима можно заменить на линейные.
Нелинейные C і L при лионеризации выбирают равным значениям в точке статического режима. Линейная модель, при действии малого сигнала, может бать получена из нелинейных для большого сигнала путем лионеризации функций в области статического режима. Линейная модель может быть получена на основе линейных эквивалентных схем.
Из полученного уравнения матрица потенциалов На основе систем или математических моделей для динамического режима можно получить необходимые качественные показатели как функции от времени. Определим как входное действие и уравнение компонентов. 3.
ЕКЗАМЕНАЦІЙНИЙ БІЛЕТ N 24 1. Анализ линейных цепей при воздействии несинусоидальных сигналов. При передачі інформації в процесі перетворення сигналів, як правило, використовуються несинусоїдальні коливання. Часто гармонічні коливання не можуть служити носіями інформації (складної інформації). При передачі повідомлень або інформації здійснюють модуляцію гармонічних коливань (модуляція за амплітудою АМ, частотоюЧМ, фазою ФМ). Використовуються також імпульсні сигнали, особливо в радіо-локації, які модулюються АІМ, ШІМ (за шириною) і ЧІМ (за ча-сом). Всі ці сигнали мають складний негармонічний характер. Передаточна несинусоїдальна функція, яка заовільняє умови Дирихле, може бути розкладена в ряд Фур¢є. f(t) = bk = Ak = Сукупнісь амлітуд в розкладі в ряд Фур¢є, відкладена навпроти відповідних частот, утворюють симетричний лінійчастий амплітуд-ний спектр; сукупність фаз – фазовий. Для неперіодичних сигналів використовують спектральне зоб-раження, яке базується на парі перетворень Фур¢є. I = Дійсне значення періодичного несинусоїдального сруму визначається дійсними значеннями Ik і не залежить від їх початкових фаз. U = P = Середня за період активна потужність дорівнює сумі дійсних потужностей гармонік. Q =
2. Детекторы АМ, ФМ, ЧМ сигналов. Особенности построения и расчета.
ЕКЗАМЕНАЦІЙНИЙ БІЛЕТ N 25 1. Метод переменных состояния и его применение при анализе ЛРЭУ и НРЭУ. Метод переменных состояния основывается на упорядоченном составлении и решении системы дифференциальных уравнений первого порядка, которые разрешены относительно производных, т.е. записаны в виде, наиболее удобном для применения численных методов интегрирования, реализуемых средствами вычислительной техники. При расчете методом переменных состояния, кроме самих уравнений состояния, связывающих первые производные Таким образом, полная система уравнений в матричной форме записи имеет вид
По законам Кирхгофа для данной цепи запишем
Поскольку
или в матричной форме записи
Матричное уравнение вида (3) вытекает из соотношений (4) и (6):
2. Усилители на ПТ с ОН, ОС и ОЗ. Усилители постоянного тока. Схема підсилювача на ПТ із ОН з індукованим n -каналом:
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 342; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.46.87 (0.01 с.) |


 = (Um* Im*cosj)/2=U*I*cosj,
= (Um* Im*cosj)/2=U*I*cosj, ; I=
; I=  .
. .
.


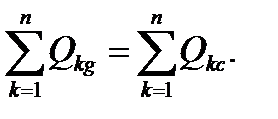
 вj = 0,
вj = 0,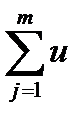 вj = 0,
вj = 0, =0.
=0. 
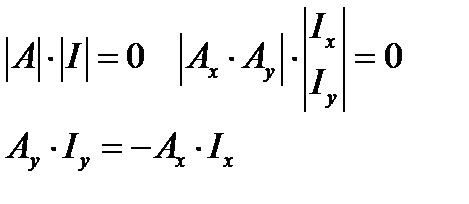
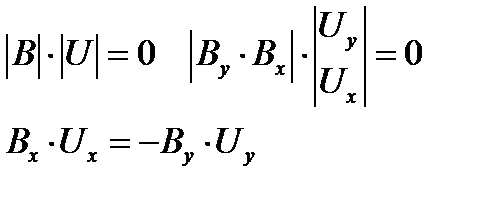 .
.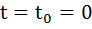 , поэтому
, поэтому 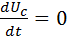 , тогда:
, тогда: 
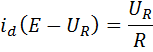
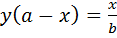 , при а=0
, при а=0 

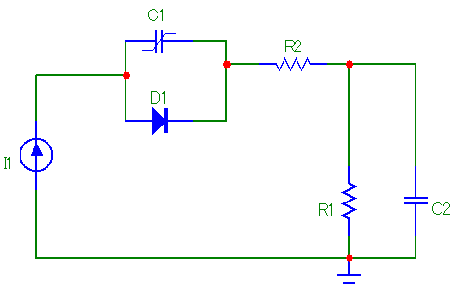 1. Модели НРЭУ для динамического режима во временной области при большом
1. Модели НРЭУ для динамического режима во временной области при большом , k бв = 0[9].
, k бв = 0[9]. w0 – резонансна частота.
w0 – резонансна частота. ; Z2=
; Z2=  .
. .Враховуючи те, що w0=
.Враховуючи те, що w0=  , отримаємо:
, отримаємо: . Легко побачити, що при R1,R2 0 wр=w0.
. Легко побачити, що при R1,R2 0 wр=w0. .
.
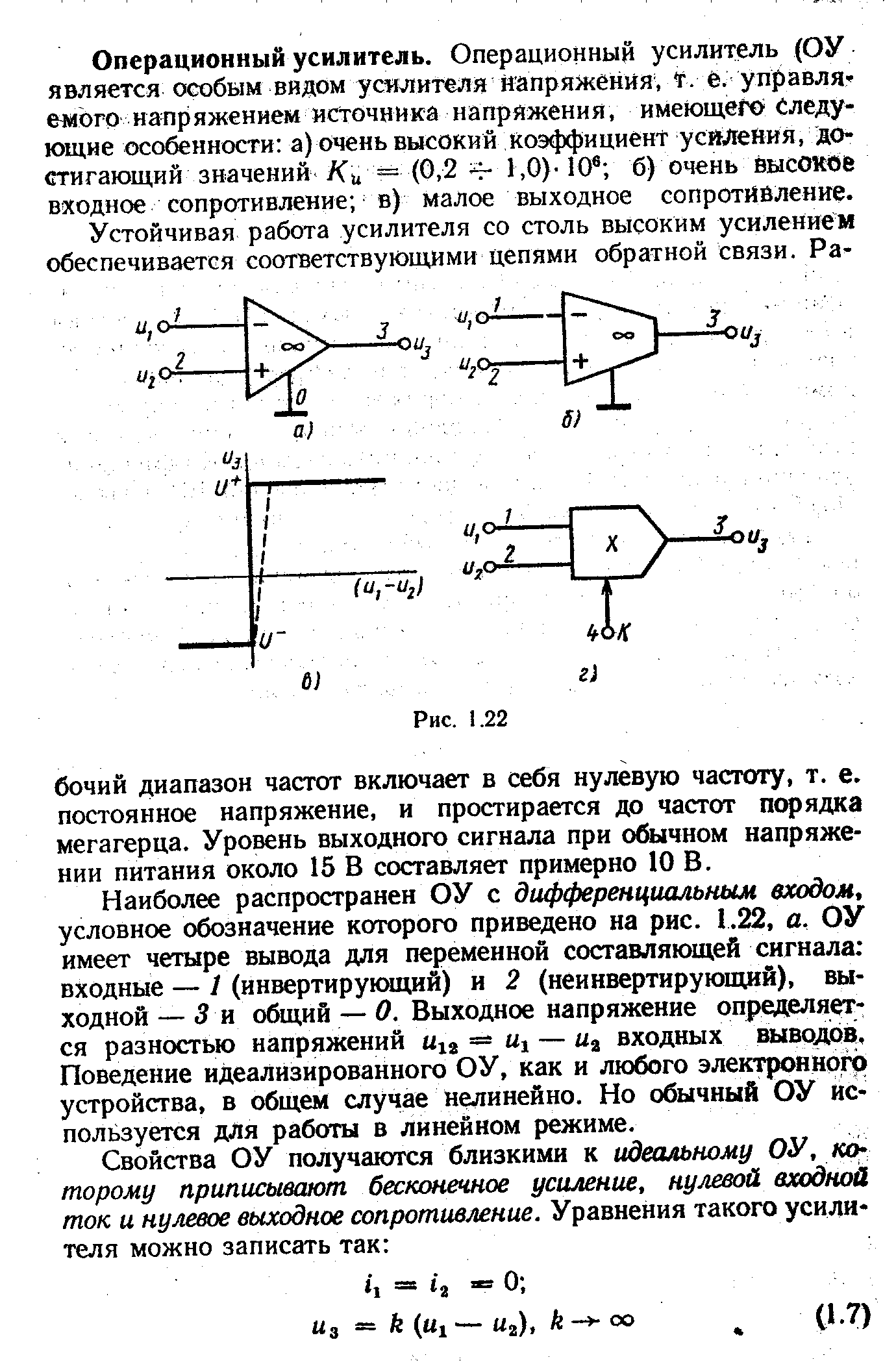

 , то можно образовать три вида модуляции: амплитудную (АМ), частотную (ЧМ) и фазовую (ФМ).
, то можно образовать три вида модуляции: амплитудную (АМ), частотную (ЧМ) и фазовую (ФМ). , то при заданной форме импульсов f0(t) можно образовать четыре основных вида импульсной модуляции: амплитудно-импульсную (АИМ), широтно-импульсную (ШИМ), время-импульсную (ФИМ) и частотно-импульсную (ЧИМ).
, то при заданной форме импульсов f0(t) можно образовать четыре основных вида импульсной модуляции: амплитудно-импульсную (АИМ), широтно-импульсную (ШИМ), время-импульсную (ФИМ) и частотно-импульсную (ЧИМ). Рассмотрим два случая:
Рассмотрим два случая: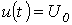 ; б)
; б) 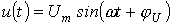
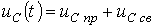
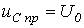
 решая которое, получаем
решая которое, получаем  . В зависимости от соотношения параметров цепи возможны три типа корней и соответственно три варианта выражения для свободной составляющей:
. В зависимости от соотношения параметров цепи возможны три типа корней и соответственно три варианта выражения для свободной составляющей: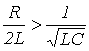 или
или  , где
, где 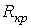 - критическое сопротивление контура, меньше которого свободный процесс носит колебательный характер. В этом случае
- критическое сопротивление контура, меньше которого свободный процесс носит колебательный характер. В этом случае 
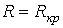 - предельный случай апериодического режима. В этом случае
- предельный случай апериодического режима. В этом случае 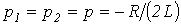 и
и 
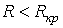 - периодический (колебательный) характер переходного процесса. В этом случае
- периодический (колебательный) характер переходного процесса. В этом случае 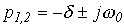 и
и  в общем случае
в общем случае  и в соответствии с первым законом коммутации, запишем для t=0 два уравнения:
и в соответствии с первым законом коммутации, запишем для t=0 два уравнения:  решая которые, получим
решая которые, получим 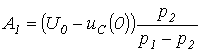
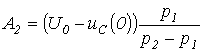
 Тогда ток в цепи
Тогда ток в цепи 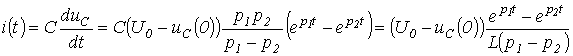
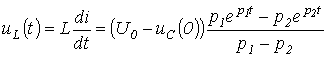

 U2І= U1ІІ;І2І= І1ІІ;
U2І= U1ІІ;І2І= І1ІІ; , то систему для складного чотириполюсника можна записати таким чином:
, то систему для складного чотириполюсника можна записати таким чином: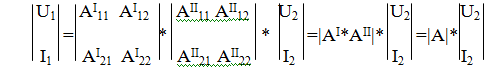




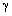 . Выходное напряжение звена обратной связи, равное:
. Выходное напряжение звена обратной связи, равное: 






 , а полоса непропускания (задерживания) – от частоты
, а полоса непропускания (задерживания) – от частоты 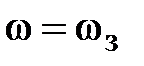 до бесконечно больших частот (рис. 2.1, а);
до бесконечно больших частот (рис. 2.1, а); , а в полосе непропускания не должно быть ниже некоторого минимально допустимого значения
, а в полосе непропускания не должно быть ниже некоторого минимально допустимого значения  .
.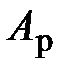 можно пересчитать в требования к АЧХ В общем виде электрические фильтры описываются передаточной функцией вида:
можно пересчитать в требования к АЧХ В общем виде электрические фильтры описываются передаточной функцией вида: 

 и, следовательно,
и, следовательно, удовлетворить заданным требования
удовлетворить заданным требования ; (2.4)
; (2.4) . (2.5)
. (2.5)



 и другие неизвестные как функции от времени.
и другие неизвестные как функции от времени. 2.
2. 
 4.
4.  5.
5. 
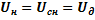 6.
6. 


 r R C
r R C +
+  w1 =
w1 =  = 2pf ak =
= 2pf ak = 

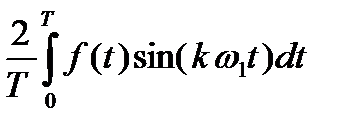 f(a) =
f(a) =  a = wt
a = wt jk = arctg
jk = arctg 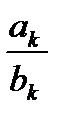 A k = Ak e-jjk A k =
A k = Ak e-jjk A k = 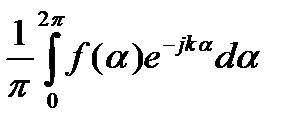
 i(t) =
i(t) = 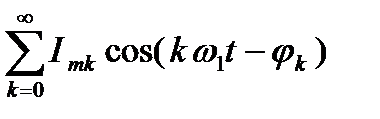 I =
I = 
 Iср =
Iср = 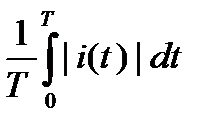
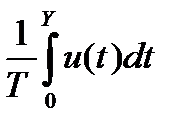 P =
P =  =
= 
 =
=  S = U × I =
S = U × I = 




 и
и  с самими переменными
с самими переменными  и
и  и источниками внешних воздействий – ЭДС и тока, необходимо составить систему алгебраических уравнений, связывающих искомые величины с переменными состояния и источниками внешних воздействий.
и источниками внешних воздействий – ЭДС и тока, необходимо составить систему алгебраических уравнений, связывающих искомые величины с переменными состояния и источниками внешних воздействий. ;
;
 .
.
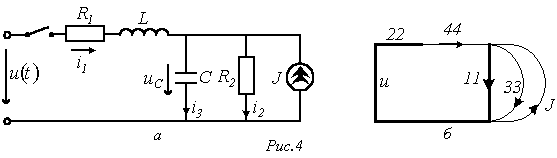
 ;
;
 ;
;
 .
.
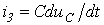 с учетом соотношения (6) перепишем уравнения (4) и (5) в виде
с учетом соотношения (6) перепишем уравнения (4) и (5) в виде
 .
. .
.


