
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проявление упругого режима. Основная формула упругого режима (по Щелкачеву В.Н.)Содержание книги
Поиск на нашем сайте
Разработка нефтяного месторождения при упругом режиме - это осуществление процесса извлечения нефти из недр в условиях, когда пластовое давление превышает давление насыщения, поля давлений и скоростей продвижения нефти и воды, насыщающих пласт, а также воды в его законтурной области неустановившиеся, изменяющиеся во времени в каждой точке пласта. Упругий режим проявляется во всех случаях, когда изменяются дебиты добывающих нефть скважин или расходы воды, закачиваемой в нагнетательные скважины. С уменьшением пластового давления до значения, меньшего, чем давление насыщения, из нефти начнет выделяться растворенный в ней газ и режим пласта изменится - упругий режим сменится режимом растворенного газа или газонапорным. Теорию упругого режима используют для решения следующих задач РНМ: 1. На основе теории упругого режима создан наиболее известный в практике разработки нефтяных месторождений метод определения параметров пласта по кривым восстановления давления в остановленных скважинах (метод КВД). 2. Гидропрослушивание скважины.Для интерпретации данных «гидропрослушивания» пласта, осуществляющегося следующим образом. В момент времени t = 0 производят, например, пуск в работу скв. А с дебитом qA На забое остановленной скв. В, в которую предварительно опускают глубинный манометр, регистрируется изм-ие заб-го давления рсв = рсв (t). 3. Расчет изменения Рпл на внешнем контуре нефтеносности или Рср по площади месторождения при разработке его в естественном режиме. 4. При расчетах восстановления давления на контуре нефтеносного пласта в случае перехода на разработку месторождения с применением заводнения или при расчетах утечки воды в законтурную область пласта, если задано давление на контуре нефтеносности. 5. Расчет определения времени выхода на установившийся режим после пуска нагнетательной скважины. Рассматривается радиальный приток жидкости к скважине с постоянным дебитом в неограниченном круговом пласте
Эта же задача при переменном дебите жидкости рассчитывается по интегралу Дюамеля.
Еi - интегрально-показательная функция.. Формулу (12) Щелкачев назвал основной формулой теории упругого режима.
26. Уравнение материального баланса. Упругий запас пласта. Расчеты упругого режима. Упругий запас пласта - это объем жидкости, который можно извлечь из пласта за счет объемной упругости пласта и насыщающих флюидов при снижении Рпл.
Уравнение материального баланса. Используется для оценки объема притока воды из законтурной водоносной области, перетоков жидкости через границу изучаемого участка пласта.
Vзак - объем закачанной воды; Qr - приток жидкости через контур;
Для того чтобы осуществлять расчеты процессов разработки нефтяных месторождений при упругом режиме, необходимо прежде всего получить дифференциальное уравнение этого режима, при выводе к-го исходят из уравнения неразрывности массы фильтрующегося вещества:
За счет деформации твердого скелета пласта при изменении напряжения изменяется пористость пласта. m = m0 - b с( s - s 0). (2) Здесь b с - сжимаемость пористой среды пласта; s 0 - начальное среднее нормальное напряжение. Используем связь между горным давлением по вертикали рГ, средним нормальным напряжением s и внутрипоровым (пластовым) давлением р. При pГ = const Учитывая (2) и (3), получим (4) Плотность фильтрующейся в пласте жидкости в первом приближении линейно зависит от давления р, т. е. (5)
где bж - сжимаемость жидкости; r0 - плотность жидкости при начальном давлении р0. Из (5) имеем(6)
Используя закон Дарси и считая проницаемость k и вязкость жидкости m не зависящими от координаты, имеем(7)
Подставим (4), (6) и (7) в (1).
|
||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 710; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.163.120 (0.006 с.) |


 Решение Щелкачева В.Н для случая работы скважины с постоянным дебитом в бесконечном круговом пласте:
Решение Щелкачева В.Н для случая работы скважины с постоянным дебитом в бесконечном круговом пласте: (12)
(12)

 - упругий запас пласта;
- упругий запас пласта; - объем добытой нефти;
- объем добытой нефти; - объем добытой воды.
- объем добытой воды.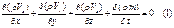 Перепишем его в виде:
Перепишем его в виде: (1)
(1)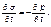 (3)
(3)

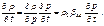

 (8)
(8) Здесь c и b - соответственно пьезопроводность и упругоемкость пласта (по предложению В. Н. Щелкачева).
Здесь c и b - соответственно пьезопроводность и упругоемкость пласта (по предложению В. Н. Щелкачева).


