Міністерство надзвичайних ситуацій України

Міністерство надзвичайних ситуацій України

Львівський державний університет безпеки життєдіяльності

Кафедра управління інформаційною безпекою

ТЕХНОЛОГІЇ ПРОГРАМУВАННЯ

Методичні вказівки і завдання
до виконання курсової роботи

Львів – 2012

ЗМІСТ

1.1. Програма роботи................................................................................ 3

1.2. Вказівки до виконання роботи......................................................... 3

1.3. Зразок виконання завдання.............................................................. 4

1.3.1. Обчислення значень елементів матриць................................... 5

1.3.2. Обчислення матричного рівняння.......................................... 13

1.3.3. Обчислення значення змінної t................................................ 18

1.3.4. Табулювання одновимірної функції....................................... 19

1.3.5. Виконання індивідуального завдання..................................... 21

Висновки та рекомендації.................................................................. 24

Додаток А. Зразок індивідуального завдання..................................... 25

Додаток Б. Зразок оформлення титульної сторінки........................... 26

Додаток В. Зразок оформлення літератури......................................... 27

Додаток Г. Код програми до виконання курсової роботи................. 28

Додаток Д. Індивідуальні завдання для виконання курсової роботи 39

Додаток Е. Приклади функції до виконання курсової роботи запрограмовані з використанням показчиків............................................................. 71

Розділ 1. Настанова з виконання курсової роботи

1.1. Програма роботи

1.1.1. Отримання бланку індивідуального завдання.

1.1.2. Усвідомлення сутності постановки задачі, складання етапів виконання роботи, теоретичний та математичний аналіз кожного з них.

1.1.3. Визначення структури програми – вхідних і вихідних даних, а також основної частини роботи.

1.1.4. Розроблення програми для виконання відповідних розрахунків згідно з вказівками до виконання завдання.

1.1.5. Підготовка власних коректних вхідних даних, проведення та аналіз отриманих результатів розрахунку.

1.1.6. Оформлення звіту про виконану роботу та захистити її.

1.2. Вказівки до виконання роботи

1.2.1. Зразок бланка індивідуального завдання наведено в дод. А. Курсант/студент, згідно з вказівкою викладача, вибирає завдання з дод. Д чи отримує від нього готове завдання.

1.2.2. Після детального ознайомлення зі змістом індивідуального завдання курсант/студент усвідомлює сутність поставленої задачі, після чого складає план послідовності етапів виконання роботи. Для кожного етапу необхідно здійснити теоретичний та математичний аналіз стосовно: виконання тих чи інших математичних дій; використання для їх реалізації стандартних функцій мови програмування С++ або стандартних програм кафедральної бібліотеки; розроблення власних функцій для реалізації елементів завдання.

1.2.3. Для реалізації наведених у завданні математичних виразів, математичних та інших дій необхідно запрограмувати відповідні функції користувача.

1.2.4. Розробити основну програму, у якій передбачити ієрархічне меню для перевірки роботи усіх функцій. Кожен пункт меню повинен виводити повідомлення з інформацією про те, що у цьому пункті буде виконуватися. Окрім цього, необхідно передбачити як введення необхідних вхідних даних за бажанням користувача, так і виведення результатів розрахунку на екран.

1.2.5. Пояснювальна записка до курсової роботи має містити такі розділи:

● титульну сторінку (див. дод. Б);

● бланк індивідуального завдання;

● реферат;

● зміст роботи;

● перелік скорочень, умовних позначень;

● вступ (актуальність роботи, мета та основні завдання);

● основна частина роботи;

● висновки та пропозиції;

● перелік використаної літератури (див. дод. В);

● додатки (результати тестових розрахунків).

1.2.6. Основна частина роботи має містити:

● розширений опис технічного завдання;

● визначення структури коду програми;

● описи відповідних функцій користувача, коди функцій, результати роботи;

● опис основної програми – призначення, меню користувача, код;

● тестування програми:

§ комплекс тестових завдань і очікувані результати розрахунку;

§ моделювання помилкових ситуацій.

1.2.7. Виконана курсова робота доповідається курсантом/студентом на засіданні відповідної комісії викладачів, затвердженої на засіданні кафедри, оцінюється за такими критеріями:

● оригінальністю підходу до розв'язання завдання;

● новизною використаних методів чи алгоритмів;

● повнотою програмної реалізації;

● оформленням пояснювальної записки;

● оригінальністю зроблених висновків та поданих пропозицій.

1.3. Зразок виконання завдання

Необхідно розробити програмне забезпечення для розв'язання математичної задачі (див. дод. Г), у якому використовуються засоби та можливості програмування у середовищі Borland C++ Builder 6. Нижче наводяться вказівки щодо виконання тільки основних особливостей розроблення такого програмного забезпечення.

Спочатку подумаємо про те, як представити вектор-стовпець, відповідні матриці та одновимірний масив протабульованих значень основної функції. Реальний підхід до розв'язання цього завдання передбачає розроблення відповідних функцій. У основній програмі передбачимо виконання таких основних функцій меню:

● введення вхідних даних;

● обчислення значень елементів МАТРИЦЬ:

§ обчислення значень елементів вектора-стовпця <С>;

§ обчислення значень елементів матриці <D>;

§ обчислення значень елементів матриці <A>;

§ обчислення значень елементів матриці <B>;

● обчислення матричного рівняння:

§ обчислення значення матричного рівняння;

§ оброблення масиву – обчислення значення t;

● обчислення значень елементів одновимірної функції:

§ часткове табулювання функції f[ x, y, z ];

§ часткове табулювання функції q[ x, y, z ];

§ табулювання функції H [ x, i, j ];

● виконання індивідуального завдання – двовимірне табулювання функції Fq [ x, y, z ] = f[ x, y, z ] + q[ x, y, z ].

Наведений перелік операцій можна використовувати як основу загальнодоступного інтерфейсу для розв'язання математичної задачі, а детальну реалізацію додаткових операцій залишимо тим, хто цим зацікавиться докладніше.

1.3.1. Обчислення значень елементів матриць

Обчислення значень елементів вектора-стовпця <С>

Елементи вектора-стовпця <С> потрібно обчислити за такою формулою:

, (1.1)

де: s – задане дійсне число; m – кількість елементів вектора; i – параметр цикла; c_i – поточне (i- те) значення елемента вектора; c_{i- 1} – попереднє (i- 1 - ше) значення елемента вектора.

З формули (1.1) видно, що кожен наступний, тобто i -ий елемент, обчислюється за допомогою функції, вхідними параметрами якої є змінна s, поточне (i- те) значення параметра циклу, а також попереднє значення елемента масиву c_{i- 1}. Отож, для обчислення значень елементів вектора-стовпця <С> можна використати такий код функції:

// Заповнення елементів вектора-стовпця < C >

void Array(double (*Fn_1)(double), double (*Fn_2)(double, double, int), double Vek[], double s, int m)

{

Vek[0] = (*Fn_1)(s);

for (int i = 1; i < m; i++)

Vek[i] = (*Fn_2)(Vek[i - 1], s, i + 1);

}

Тут формальними параметрами є дві функції: перша функція дає змогу обчислити перше значення елемента одновимірного масиву c ₁ = f [ s ]; друга функція обчислює наступні значення елементів одновимірного масиву c_і = f [ s, i, c_{i- 1}]. Значення змінних s та m також є формальними параметрам. Внаслідок роботи функції на виході отримаємо елементи одновимірного масиву, тобто вектора-стовпця <С>.

Значення елементів вектора-стовпця <С> потрібно обчислити за такими формулами:

; , (1.2)

де: s – задане дійсне число; i – параметр циклу; c ₁ та c_i – перше та i- те значення елемента вектора; c_{i- 1} – попереднє (i- 1 - ше) значення елемента вектора.

З формул (1.2) видно, що 1-ий елемент вектора-стовпця обчислюється за однією функцією, вхідним параметром якої є змінна s. Кожен i -ий елемент обчислюється за іншою функцією, вхідними параметрами якої є змінна s, поточне (i- те) значення параметра циклу, а також попереднє значення елемента вектора-стовпця c_{i- 1}. Отож, для обчислення значень елементів вектора-стовпця можна використати такі коди функції:

// Обчислення першого значення елемента одновимірного масиву < C >

double Fn_c1(double s)

{

double c11 = pow (s, 1.2);

double c12 = pow (cos (s + 1), 2);

double c13 = (pow (s, 0.23) + 3/s);

return c11 + pow (c12/c13, 1./3);

}

 

// Обчислення поточного значення елемента одновимірного масиву < C >

double Fn_ci(double Cp, double s, int i)

{

double c1 = pow (fabs (Cp), s/i);

double c2 = pow (i, 0.3)/ pow (s, i/s);

double c3 = (s * s - pow (i, 0.2))/(Cp - s);

double c4 = pow (pow (Cp, 2), 1./i);

return c1 + c2 * (c3 - c4);

}

Параметризована функція Fn_Show() призначена для виведення елементів одновимірного масиву. Як видно з прототипу функції, її параметрами є одновимірний масив, його ім'я та розмір.

// Заповнення елементів вектора-стовпця < C >

void Array(double (*Fn_1)(double), double (*Fn_2)(double, double, int), double Vek[], double s,

int m)

{

Vek[0] = (*Fn_1)(s);

for (int i = 1; i < m; i++)

Vek[i] = (*Fn_2)(Vek[i - 1], s, i + 1);

}

У наведеному нижче коді програми продемонстровано механізм обчислення значень елементів одновимірного масиву, а також механізм заповнення елементів вектора-стовпця <C>.

Код програми 1.1. Демонстрація механізму заповнення елементів вектора-стовпця <C>

// Курсова робота, v.9

# include < vcl >

# include < conio > // Для консольного режиму роботи

# include < math >

# include < iomanip >

# include < iostream > // Для потокового введення - виведення

using namespace std; // Використання стандартного простору імен

 

const int sizeM = 5, sizeN = 10; // Оголошення констант

 

// Обчислення першого значення елемента одновимірного масиву < C >

double Fn_c1(double s);

// Обчислення поточного значення елемента одновимірного масиву < C >

double Fn_ci(double Cp, double s, int i);

// Заповнення елементів вектора-стовпця < C >

void Array(double (*Fn_1)(double), double (*Fn_2)(double, double, int), double Vek[], double s,

int m);

...........

 

int main ()

{

cout. precision (3); // Формат #.###

cout. setf (ios_base::fixed); // Формат #.###

SetConsoleOutputCP(1251); // Виведення кирилиці

 

cout << "Курсова робота, варіант №9" << endl;

// Оголошення змінних

int m; cout << "Введіть значення m = "; cin >> m;

int n; cout << "Введіть значення n = "; cin >> n;

double s, t; cout << "Введіть значення s = "; cin >> s; cout << endl;

double A[sizeM][sizeM], B[sizeM][sizeM], C[sizeM], D[sizeM][sizeM], H[sizeN], X[sizeM][sizeM];

double Temp1[sizeM][sizeM], Temp2[sizeM][sizeM], Bs[sizeM][sizeM];

 

Array(Fn_c1, Fn_ci, C, s, m);

Fn_Show("1. Обчислення значень елементів вектора-стовпця < C > ", C, m);

...........

getch (); return 0;

}

Внаслідок виконання ця програма відображає на екрані такі результати розрахунку:

Обчислення значень елементів матриць <D>, <A> і <B>

Елементи матриці <D> потрібно обчислити за такою формулою:

, (1.3)

де: m – кількість рядків і стовпців матриці; i,j – параметри циклів; d_ij – поточне значення елемента, яке знаходиться в i -му рядку та j -му стовпці матриці; c_i (c_j) – значення i -ого (j -ого) елемента вектора <С>.

З формули (1.3) видно, що елементи матриці <D> можна обчислити за допомогою коду функції, вхідними параметрами якої є: функція для обчислення поточного значення елемента матриці; вектор-стовпець <С>; розмір матриці. Отож, для обчислення значень елементів матриці <D> можна використати такий код функції:

// Заповнення елементів матриці < D >

void Array(double (*Fn_1)(double, double), double Mat[][sizeM], double Vek[], int m, int n)

{

for (int i = 0; i < m; i++)

for (int j = 0; j < m; j++)

Mat[i][j] = (*Fn_1)(Vek[i], Vek[j]);

}

Внаслідок роботи функції на виході отримаємо елементи двовимірного масиву, тобто матриці <D>.

З формули (1.3) видно, що поточний елемент матриці можна обчислити за допомогою функції, вхідними параметрами якої мають бути дві змінні – значення i -ого та j -ого елементів вектора <С>. Отож, для обчислення значень елементів матриці можна використати такий код функції:

// Обчислення поточного значення елемента двовимірного масиву < D >

double Fn_dij(double ci, double cj)

{

double d1 = ci + 1.3 * cj;

double d2 = pow (ci, 2) + 1.65;

double d3 = ci/cj;

double d4 = cos (pow (fabs (d1/d2), 0.136));

double d5 = sin (pow (fabs (d3), 1.34));

return d4 + d5;

}

Елементи матриці <A> потрібно обчислити за такою формулою:

, (1.4)

де: m – кількість рядків і стовпців матриці; i,j – параметри циклів; a_ij – поточне значення елемента, яке знаходиться в i -му рядку та j -му стовпці матриці.

З формули видно, що елементи матриці <A> можна обчислити за допомогою функції, вхідними параметрами якої є: функція для обчислення поточного значення елемента матриці; кількість рядків і стовпців матриці. Отож, для обчислення значень елементів матриці <D> можна використати такий код функції:

// Заповнення елементів матриці < A >

void Array(double (*Fn_1)(int, int), double Mat[][sizeM], int m, int n)

{

for (int i = 0; i < m; i++)

for (int j = 0; j < m; j++)

Mat[i][j] = (*Fn_1)(i + 1, j + 1);

}

Внаслідок роботи функції на виході отримаємо елементи двовимірного масиву, тобто матрицю <A>. Значення елементів матриці <A> потрібно обчислити за такою формулою:

, (1.5)

де i,j – параметри циклів.

З формул (1.5) видно, що елемент, який знаходиться на перетині i -го рядка та j -го стовпця, можна обчислити за допомогою логічного оператора, вхідними параметрами якого є значення параметрів зовнішнього і внутрішнього циклів. Отож, для обчислення значень елементів матриці можна використати такий код функції:

// Обчислення поточного значення елемента двовимірного масиву < A >

double Fn_aij(int i, int j)

{

if (i == j)

{

double a1 = pow (j, i/2.);

double a2 = pow (sin (pow (i, 1.3)), 2);

double a3 = pow (j + a2, 1./(i + 1));

return a1 + a3;

}

else if (i < j)

{

double a1 = pow (i, 2./j);

double a2 = i * i + (double)i/j;

double a3 = j + pow (i, 1.3)/3;

double a4 = pow (log ((double)i/j), 2);

return a1 + a2/a3 - a4;

}

Else

{

double a1 = pow (j, (double)i/j);

double a2 = pow (log (pow (i, 1.2) + j), 0.3);

return a1 - a2;

}

}

Елементи матриці <B> потрібно обчислити за такою формулою:

, (1.6)

де: m – кількість рядків і стовпців матриці; i,j – параметри циклів; b_ij – поточне значення елемента, яке знаходиться в i -му рядку та j -му стовпці матриці.

З формули видно, що елементи матриці <B> можна обчислити за допомогою функції, вхідними параметрами якої є: функція для обчислення поточного значення елемента матриці; задане дійсне число s; кількість рядків і стовпців матриці. Отож, для обчислення значень елементів матриці <B> можна використати такий код функції:

// Заповнення елементів матриці < B >

void Array(double (*Fn_1)(int, int, double), double Mat[][sizeM], double s, int m, int n)

{

for (int i = 0; i < m; i++)

for (int j = 0; j < n; j++)

Mat[i][j] = (*Fn_1)(i + 1, j + 1, s);

}

Внаслідок роботи функції на виході отримаємо елементи двовимірного масиву, тобто матриці <B>. Значення елементів матриці <B> потрібно обчислити за такою формулою:

, (1.7)

де i,j – параметри циклів.

З формул (1.5) видно, що елемент, який знаходиться на перетині i -го рядка та j -го стовпця, можна обчислити за допомогою логічної функції, вхідними параметрами якої є значення параметрів зовнішнього і внутрішнього циклів, а також задане дійсне число. Отож, для обчислення значень елементів матриці можна використати такий код функції:

// Обчислення поточного значення елемента двовимірного масиву < B >

double Fn_bij(int i, int j, double s)

{

double bs = 0, sum = 0, c = 0;

int z = 1, h = 1;

do

{

bs += z * c; sum = 0;

for (int k = 1; k <= i + 1; k++)

{

double sum1 = k * pow (s, (double)h/i)/(h/s);

double sum2 = (double)i/j;

sum += pow (log (sum1 + sum2), 1.22);

}

c = sum/(Fact(h) + pow (fabs (s/i - 1.23 * j), j + 1));

h++; z = -z;

} while (fabs (c) > 0.0001);

return bs;

}

Функція Fn_Show() призначена для виведення елементів двовимірного масиву, покажчик на який передається цій функції як параметр. Також параметром цієї функції є цілочисельна змінна m, що вказує на розмір масиву.

// Відображення елементів двовимірного масиву

void Fn_Show(char *name, double Mas[][sizeM], int m, int n, int z)

{

cout << name << endl;

for (int i = 0; i < m; i++)

{

for (int j = 0; j < n; j++)

cout << setw (z) << Mas[i][j];

cout << endl;

}

cout << " --- " << endl << endl;

}

 

// Відображення елементів одновимірного масиву

void Fn_Show(char *name, double Vek[], int m, int z)

{

cout << name << endl;

for (int i = 0; i < m; i++)

cout << setw (3) << i << " -- > " << setw (z) << Vek[i] << endl;

cout << " --- " << endl << endl;

}

Для впорядкування за зростанням значень елементів рядків відповідних матриць доцільно розробити функцію, яка б давала змогу упорядкувати елементи одновимірного масиву, наприклад, методом пошуку найменшого елемента (за зростанням значень елементів). Функція Sort_min() слугує для упорядкування елементів рядків двовимірного масиву методом пошуку найменшого елемента, покажчик на який передається їй як параметр. Також параметром даної функції є цілочисельна змінна m, що вказує розмір масиву.

// Упорядкування рядків двовимірного масиву методом пошуку мінімальних елементів

void Sort_min(double Mat[][sizeM], int m, int n)

{

int j = 0;

while (j < m)

{

int start = 0;

while (start < m)

{

double min = Mat[j][start];

int pos = start;

for (int i = start; i < m; i++)

if (min > Mat[j][i])

{

min = Mat[j][i];

pos = i;

}

Mat[j][pos] = Mat[j][start];

Mat[j][start] = min;

start++;

}

j++;

}

}

 

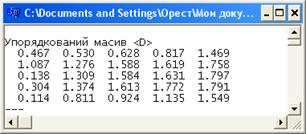
// Обчислення значення факторіалу

double Fact(double n)

{

double f = 1;

for (int i = 1; i <= n; i++) f *= i;

return f;

}

У наведеному нижче коді програми продемонстровано механізм обчислення значень елементів двовимірних масивів, а також механізм заповнення елементів матриць <D>, <A> і <B>.

Код програми 1.2. Демонстрація механізму заповнення елементів матриць <D>, <A> і <B>

...........

double Fn_dij(double ci, double cj);

// Заповнення елементів матриці < D >

void Array(double (*Fn_1)(double, double), double Mat[][sizeM], double Vek[], int m, int n);

// Обчислення поточного значення елемента двовимірного масиву < A >

double Fn_aij(int i, int j);

// Заповнення елементів матриці < A >

void Array(double (*Fn_1)(int, int), double Mat[][sizeM], int m, int n);

// Обчислення поточного значення елемента двовимірного масиву < B >

double Fn_bij(int i, int j, double s);

// Заповнення елементів матриці < B >

void Array(double (*Fn_1)(int, int, double), double Mat[][sizeM], double s, int m, int n);

// Відображення елементів одновимірного масиву

void Fn_Show(char *name, double Vek[], int m, int z = 7);

// Відображення елементів двовимірного масиву

void Fn_Show(char *name, double Mas[][sizeM], int m, int n, int z = 9);

// Упорядкування рядків двовимірного масиву методом пошуку мінімальних елементів

void Sort_min(double Mat[][sizeM], int m, int n);

// Обчислення значення факторіалу

double Fact(double n);

...........

int main()

{

...........

cout << "2. Обчислення значень елементів двовимірного масиву < D > " << endl;

Array(Fn_dij, D, C, m, m);

Fn_Show("Масив < D > ", D, m, m); // Виведення елементів двовимірного масиву

Sort_min(D, m, m); // Впорядкування за зростанням значень елементів рядків матриці

Fn_Show("Упорядкований масив < D > ", D, m, m); // Виведення елементів двовимірного масиву

 

cout << "3. Обчислення значень елементів двовимірного масиву < A > " << endl;

Array(Fn_aij, A, m, m);

Fn_Show("Масив < A > ", A, m, m); // Виведення елементів двовимірного масиву

Sort_min(A, m, m); // Впорядкування за зростанням значень елементів рядків матриці

Fn_Show("Упорядкований масив < A > ", A, m, m); // Виведення елементів двовимірного масиву

 

cout << "4. Обчислення значень елементів двовимірного масиву < B > " << endl;

Array(Fn_bij, B, s, m, m);

Fn_Show("Масив < B > ", B, m, m); // Виведення елементів двовимірного масиву

Sort_min(B, m, m); // Впорядкування за зростанням значень елементів рядків матриці

Fn_Show("Упорядкований масив < B > ", B, m, m); // Виведення елементів двовимірного масиву

...........

getch (); return 0;

}

Внаслідок виконання ця програма відображає на екрані такі результати розрахунку:

1.3.2. Обчислення матричного рівняння

Для обчислення матричного рівняння

необхідно запрограмувати функції, які би давали змогу виконували основні дії над матрицями, зокрема:

● присвоєння матриць;

● додавання / віднімання векторів;

● додавання / віднімання матриць;

● множення матриці на матрицю;

● множення матриці на число;

● піднесення матриці до n-го степеня;

● обчислення транспонованої матриці;

● обчислення оберненої матриці.

Отож, для обчислення матричного рівняння можна використати такі коди функцій:

// Присвоєння значень елементів однієї матриці іншій

void Appropriation(double Mat1[][sizeM], double Mat2[][sizeM], int m, int n)

{

for (int i = 0; i < m; i++)

for (int j = 0; j < n; j++)

Mat1[i][j] = Mat2[i][j];

}

 

// Присвоєння значень елементів одного вектора іншому

void Appropriation(double vek1[], double vek2[], int m)

{

for (int i = 0; i < m; i++) vek1[i] = vek2[i];

}

 

// Виконання дії додавання "+" двох матриць

void Addition(double Mat1[][sizeM], double Mat2[][sizeM], double Mat3[][sizeM], int m, int n)

{

for (int i = 0; i < m; i++)

for (int j = 0; j < n; j++)

Mat3[i][j] = Mat1[i][j] + Mat2[i][j];

}

 

// Виконання дії додавання "+" двох векторів

void Addition(double Vek1[], double Vek2[], double Vek3[], int m)

{

for (int i = 0; i < m; i++)

Vek3[i] = Vek1[i] + Vek2[i];

}

 

// Виконання дії віднімання "-" двох матриць

void Deduction(double Mat1[][sizeM], double Mat2[][sizeM], double Mat3[][sizeM], int m, int n)

{

for (int i = 0; i < m; i++)

for (int j = 0; j < n; j++)

Mat3[i][j] = Mat1[i][j] - Mat2[i][j];

}

 

// Виконання дії віднімання "-" двох векторів

void Deduction(double Vek1[], double Vek2[], double Vek3[], int m)

{

for (int i = 0; i < m; i++)

Vek3[i] = Vek1[i] - Vek2[i];

}

 

// Виконання дії множення "*" матриці на матрицю

void Increase(double Mat1[][sizeM], double Mat2[][sizeM], double Mat3[][sizeM], int m, int n)

{

double s = 0;

double temp[sizeM][sizeM];

for (int i = 0; i < m; i++)

for (int j = 0; j < n; j++)

{

s = 0;

for (int k = 0; k < m; k++)

s += Mat1[i][k] * Mat2[k][j];

temp[i][j] = s;

}

Appropriation(Mat3, temp, m, m);

}

 

// Виконання дії множення "*" матриці на число

void Increase(double Mat1[][sizeM], double variable, double Mat2[][sizeM], int m, int n)

{

for (int i = 0; i < m; i++)

for (int j = 0; j < n; j++)

Mat2[i][j] = Mat1[i][j] * variable;

}

 

// Піднесення матриці до n - го степеня

void MStep(double Mat1[][sizeM], int variable, int m)

{

int step;

double temp[sizeM][sizeM];

Appropriation(temp, Mat1, m, m);

if (variable >= 2)

{

step = 1;

while (step < variable)

{

Increase(temp, Mat1, temp, m, m); step++;

}

Appropriation(Mat1, temp, m, m);

}

}

 

// Обчислення транспонованої "^t" матриці

void Transp(double Mat1[][sizeM], int m, int n)

{

double temp[sizeM][sizeM];

Appropriation(temp, Mat1, m, n);

for (int i = 0; i < m; i++)

for (int j = 0; j < n; j++)

Mat1[j][i] = temp[i][j];

}

 

// Обчислення оберненої " - 1" матриці

void MOBR(double Mat[][sizeM], int n)

{

int i, j, K, temp1[sizeM];

double temp2[sizeM], temp3[sizeM];

double Y, D = 1.0, w, E = 0.000000000001;

for (j = 0; j < n; j++) temp1[j] = j;

for (i = 0; i < n; i++)

{

K = i; Y = Mat[i][i];

for (j = i + 1; j < n; j++)

{

w = Mat[i][j];

if (fabs (w) > fabs (Y))

{

K = j; Y = w;

}

}

D *= Y;

if (fabs (Y) < E) exit (1);

for (j = 0; j < n; j++)

{

temp2[j] = Mat[j][K]; Mat[j][K] = Mat[j][i];

Mat[j][i] = -temp2[j]/Y; Mat[i][j] = Mat[i][j]/Y;

temp3[j] = Mat[i][j];

}

Mat[i][i] = 1/Y; j = temp1[i]; temp1[i] = temp1[K]; temp1[K] = j;

for (K = 0; K < n; K++)

if (K!= i)

for (j = 0; j < n; j++)

if (j!= i)

Mat[K][j] = Mat[K][j] - temp3[j] * temp2[K];

}

for (i = 0; i < n; i++)

{

K = temp1[i];

if (K!= i)

{

for (j = 0; j < n; j++)

{

w = Mat[i][j]; Mat[i][j] = Mat[K][j]; Mat[K][j] = w;

}

j = temp1[i]; temp1[i] = temp1[K]; temp1[K] = j; D = -D;

}

}

}

Для збереження проміжних результатів розв'язування матричного рівняння ми скористаємося наперед оголошеними масивами <As> та <Bs>. Розв'язком матричного рівняння є матриця яка поміщається в масив <X>.

У наведеному нижче коді програми продемонстровано механізм обчислення матричного рівняння.

Код програми 1.3. Демонстрація механізму обчислення матричного рівняння

...........

// Присвоєння значень елементів одного вектора іншому

void Appropriation(double vek1[], double vek2[], int m);

// Виконання дії додавання "+" двох матриць

void Addition(double Mat1[][sizeM], double Mat2[][sizeM], double Mat3[][sizeM], int m, int n);

// Виконання дії додавання "+" двох векторів

void Addition(double Vek1[], double Vek2[], double Vek3[], int m);

// Виконання дії віднімання "-" двох матриць

void Deduction(double Mat1[][sizeM], double Mat2[][sizeM], double Mat3[][sizeM], int m, int n);

// Виконання дії віднімання "-" двох векторів

void Deduction(double Vek1[], double Vek2[], double Vek3[], int m);

// Виконання дії множення "*" матриці на матрицю

void Increase(double Mat1[][sizeM], double Mat2[][sizeM], double Mat3[][sizeM], int m, int n);

// Виконання дії множення "*" матриці на число

void Increase(double Mat1[][sizeM], double variable, double Mat2[][sizeM], int m, int n);

// Піднесення матриці до n - го степеня

void MStep(double Mat1[][sizeM], int variable, int m);

// Обчислення транспонованої "^t" матриці

void Transp(double Mat1[][sizeM], int m, int n);

// Обчислення оберненої " - 1" матриці

void MOBR(double Mat[][sizeM], int n);

...........

int main ()

{

...........

cout << "5. Розв'язання матричного рівняння" << endl;

cout << " < A * X = 3.5 * B^2 + D^t - 2 * A > " << endl;

Appropriation(Temp1, B, m, m);

MStep(Temp1, 2, m);

Fn_Show(" < B^2 > ", Temp1, m, m);

 

Increase(Temp1, 3.5, Temp1, m, m);

Fn_Show(" < 3.5 * B^2 > ", Temp1, m, m);

 

Appropriation(Temp2, D, m, m);

Transp(Temp2, m, m);

Fn_Show(" < D^t > ", Temp2, m, m);

 

Addition(Temp1, Temp2, Temp1, m, m);

Fn_Show(" < 3.5 * B^2 + D^t > ", Temp1, m, m);

 

Appropriation(Temp2, A, m, m);

Increase(Temp2, 2, Temp2, m, m);

Fn_Show(" < 2 * A > ", Temp2, m, m);

 

Deduction(Temp1, Temp2, Bs, m, m);

Fn_Show(" < Bs = 3.5 * B^2 + D^t - 2 * A > ", Bs, m, m);

 

Appropriation(Temp2, A, m, m);

MOBR(Temp2, m);

Fn_Show(" < A^ - 1 > ", Temp2, m, m);

 

Increase(Temp2, Bs, X, m, m);

Fn_Show("Масив < X = A^ - 1 * Bs > ", X, m, m, 9);

 

Increase(A, X, Bs, m, m);

Fn_Show("Перевірка < A * X = Bs > ", Bs, m, m, 9);

...........

getch (); return 0;

}

Внаслідок виконання ця програма відображає на екрані такі результати розрахунку:

1.3.3. Обчислення значення змінної t

Для обчислення значення змінної t – квадрату найменшого із середньоарифметичних значень додатних елементів кожного із стовпців матриці X, які мають непарні номери, розроблено спеціальну функцію znach_tt(), як параметри у дану функцію передаються покажчик на двовимірний масив та цілочисельна змінна яка вказує на розмір масиву.

Отож, для обчислення значення змінної t можна використати такий код функцій:

// Обчислення значення змінної t

double znach_tt(double Mat1[][sizeM], int n)

{

double temp[sizeM], min, s;

int h = 0, k;

for (int j = 0; j < n; j += 2)

{

s = 0; k = 0;

for (int i = 0; i < n; i++)

if (Mat1[i][j] > 0)

{

s += Mat1[i][j]; k++;

}

if (k > 0)

{

s = s/k; temp[h++] = s;

}

}

min = temp[0];

for (int j = 0; j < h; j++)

if (min > temp[j]) min = temp[j];

return pow (min, 2);

}

У наведеному нижче коді програми продемонстровано механізм обчислення значення змінної t.

Код програми 1.4. Демонстрація механізму обчислення значення змінної t

...........

// Обчислення значення змінної t

double znach_tt(double Mat1[][sizeM], int n);

...........

 

int main ()

{

...........

cout << "6. Обчислення значення змінної t" << endl << endl;

cout << "t = " << (t = znach_tt(X, m)) << endl << endl;

...........

getch (); return 0;

}

Внаслідок виконання ця програма відображає на екрані такі результати розрахунку:

1.3.4. Табулювання одновимірної функції

Для того щоб виконати табулювання одновимірної функції H потрібно запрограмувати математичні функції f та q які є одними із параметрів функції H. Функції користувача Fn_f() та Fn_q() повертають нам значення функцій f та q відповідно. Функція Mas_H() призначена для обчислення та виведення кінцевого та проміжних результатів значення математичної функції hi = f [i, t, s] та заповнення елементами масиву <H>. Параметрами даної функції є функції Fn_f() та Fn_q(), цілочисельна змінна i, змінні t і s типу double

Отож, для табулювання одновимірної функції можна використати такі коди функцій:

// Обчислення значення функції f

double Fn_f(double x, double y, double z)

{

double f1 = 3 + exp (y - x);

double f2 = sqrt (pow (fabs (y * y + x), 0.3));

double f3 = 1 + (x * x) * fabs (y - sin (pow (fabs (z), 0.42)));

return (f1 + f2)/f3;

}

 

// Обчислення значення функції q

double Fn_q(double x, double y, double z)

{

double q1 = y/z;

double q2 = (y - pow (fabs (z), 0.3))/(1.2 + x * x);

double q3 = pow (tan ((2 * x - 1.4)/(x + (z * z))), 2);

double q4 = z * exp (-(x - y)/(z + 1.1));

return q1 * pow (fabs (q2 - q3), 1.65) - q4;

}

 

// Обчислення значень одновимірного масиву < H >

void Mas_H(double (*Fn_1)(double, double, double), double (*Fn_2)(double, double, double),

double Vek[], double t, double s, int n)

{

cout << setw (4) << "Hi" << setw (10) << "f1" << setw (14) << "f2" << setw (10) << "f3"

<< setw (10) << "f4" << setw (12) << "hi" << endl;

for (int i = 1; i <= n; i++)

{

double f11 = (*Fn_1)(t/i, pow (fabs (- 2 * s), 0.2), 1.17 * i); f11 = f11 * f11;

double f12 = pow (sin (t * s/i), 2);

double f1 = f11 + f12;

cout << "H[" << i - 1 << "] = " << setprecision (3) << setw (10) << f1;

 

double f21 = (*Fn_2)(1.2 * t/i, pow (fabs (i - t/s), 0.12), s/i - 1.7); f21 = fabs (f21);

double f22 = pow (t, i/s);

double f2 = pow (fabs (f21 - f22), 1.3/i);

cout << setw (10) << f2;

 

double f3 = (*Fn_2)(i/s, pow (fabs (s - t/i), 0.12), s/i - t);

cout << setw (10) << f3;

 

double f4 = (*Fn_1)(i * i, s * pow (t, s/i), s - t * t); f4 = pow (pow (fabs (f4), 1.2), 1./i + 1);

cout << setw (10) << f4;

 

Vek[i - 1] = f1/f2 + f3/f4;

cout << setw (12) << Vek[i - 1] << endl;