Основы проектирования валов гтд.

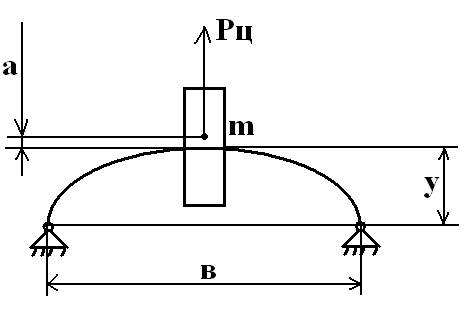
Валы авиационных двигателей имеют один или несколько дисков, которые на больших частотах вращения могут изгибаться. Работа на данных частотах вращения сопровождается большими вибрациями, а сами частоты вращения называются критическими. Длительная работа на этих частотах может привести к аварии. Опыт эксплуатации показывает, что при увеличении частоты вращения вала выше критической, вибрация резко уменьшается, т.е., если перейти быстро через критическую частоту вращении, то при некотором удалении от этой частоты вращения, двигатель может снова работать без больших вибраций. Следовательно, в авиационных двигателях валы роторов работающих на частотах вращения меньше критической называются жесткими валами, а валы, работающие на частотах вращения выше критической, называются гибкими.

Для того, чтобы разобраться в явлении вибрации и выяснить почему с увеличением частоты вращения прогиб вала увеличивается, необходимо изобразить простейшую схему вала на двух опорах с одним диском, при условии, что вал невесомый, а диск расположен ровно посередине. Подшипники скольжения или качения расположенные в опорах вала не мешают прогибу вала. Также на вал не влияют силы, возникающие из-за массы вала и диска.

ω < ωкр

 

m – масса диска, y – прогиб, a – расстояние между центром тяжести вала и осью прогнувшегося вала.

При вращении вала на диск с валом действует центробежная сила Pц.

 

Pц = m * (y + a) * ω²

При установившемся движении существует равновесие между центробежной силой упругости вала:

 

P = c * y

m * (y + a) * ω² = c * y

 

Где с коэффициент жесткости вала, равный силе, приложенной УК валу, чтобы получить прогиб, равный единице. Из этого выражения можно получить формулу прогиба вала:

 

y = m * a * ω² / c – m * ω²

 

Согласно этому выражению можно построить зависимость изменения прогиба вала в зависимости от ω:

 

Согласно приведенным зависимостям инерционная сила увеличивается пропорционально прогибу, если рассмотреть последнюю зависимость, то прогиб равен бесконечности, если знаменатель обращается в нуль:

 

c – m * ω² = 0

 

 

При частоте вращения равной критической, инерционная сила преобладает над силой упругости и равновесное состояние разрушается. Вал теряет устойчивость и прогиб вала неограниченно возрастает, поэтому скорость, при которой вал теряет устойчивой, называется критической. Пи скорости вращения выше критической, равновесное состояние вала восстанавливается, положение центра тяжести меняется:

 

 

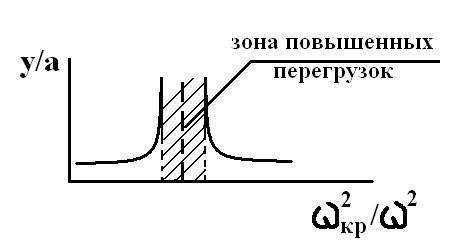
Т.е. при увеличении скорости вращения больше критической происходит уменьшение прогиба вала, который стремится в своем пределе к расстоянию между центром тяжести и осью вала. Это означает, что центр масс диска стремится занять положение на оси вращения ротор. Это означает, что при увеличении скорости вращения больше критической, имеет место тенденция самоцентровки ротора. Очевидно, что критическая скорость ротора зависит только от соотношения коэффициента жесткости диска и массы диска, т.е. от конструктивных размеров вала с диском. Следовательно, критическая скорость ротора является его динамической характеристикой, поэтому роторы, работающего в режиме жесткого вала, состояние равновесия является статическим, т.е. для таких валов характерно увеличение прогибов и усилий, которые действуют на опоры при увеличении угловой скорости. Роторы, работающие в режиме гибкого вала, находятся в состоянии устойчивого динамического равновесия. Рабочие угловые скорости валов не должны быть близкими к критической скорости. Диапазон, в котором не должны лежать рабочие скорости определяется допустимым прогибом ротора. Для расчета этой зоны строится диаграмма согласно зависимости относительного прогиба ротора от отношения скорости к критической:

 

y / a = 1 / (ωкр² / ω²) – 1.

 

 

 

Согласно этой диаграмме можно судить о зависимости величины относительно прогиба вала и скорости вала. При высокой степени балансировки ротора можно допустить большую величину относительного прогиба. В этом случае зона повышенных перегрузок будет уже. Однако, разница между скоростью вращения ротора и величиной критической скорости не может быть меньше плюс/минус 10% т.к. далее возникает интенсивный рост прогиба вала, т.е. его разрушение роторы современных двигателей из-за легкой конструкции и малой жесткости относятся к гибким валам, поэтому их рабочие скорости лежат выше критических. Для таких роторов проход зоны критической скорости при разгоне ротора и его торможении должен происходить с большим ускорением и торможением. Для того, чтобы время прохождения зоны было минимальным необходимо также предусмотреть, чтобы увеличение прогиба ротора в период прохождения критической скорости был незначительным. Приведенная зависимость показывает, то критическая скорость вращения ротора совпадает с частотой собственных колебаний.