
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Definitions and basic properties of antiquaternionsСодержание книги
Поиск на нашем сайте
It is known [1, 2], the four-dimensional hypercomplex numerical system called a system of quaternions
. Quaternions are the result of anticommutative doubling of complex numbers
If we redouble the system of complex numbers
,
we obtain a system of antiquaternions
Indeed, if we take the composition of bases
We will give some examples of multiplication of basic elements, taking into account these rules:
If to rename two-symbolical names of basic elements in one-symbolical:
то that we will receive the multiplication table of basic elements of system of antiquaternions:
(3)
The principle of multiplication of basic elements is represented in fig. 1, on which basic elements
Fig. 1 Schematic image of the multiplication table of basic elements of antiquaternion’s system.
Thus, anti-quaternions are numbers of a look
where:
Addition and multiplication of antiquaternions In system of anti-quaternions is entered addition and multiplication operations thus: The antiquaternion is called the sum of two antiquaternions The antiquaternion
is called the product of two antiquaternions
According to rules of addition and multiplication of antiquaternions it is possible to mark out their main properties: 1) operation of addition is commutative: 2) operation of addition is associative: 3) operation of multiplication is noncommutative: Really:
but opposite order is such as:
That is carried out (6). 4) operation of multiplication is associative: It can be proved directly, using (5). 5) In the same way it is possible to prove the distributivity of antiquaternions: 6) for antiquaternions is determined action of multiplication by a scalar:
7) for
Definition of norm of antiquaternions
In the work [2] the norm of hypercomplex number generally is determined by a formula
where
Having calculated a determinant of a matrix (8) we will receive norm of hypercomplex numbers
By analogy to the theory of quaternions we will call a root of the norm a pseudonorm of anti-quaternions (9), which will be denoted as
Apparently from (10), the pseudonorm can be negative. It is possible to show that the pseudonorm entered by such method is multiplicative:
Definition and characteristics of conjugate antiquaternions We introduce the definition of conjugate antiquaternion
on the basis of equality
as it is offered in [2]. If (13) substitute (5) and (10), and to equate coefficients at identical basic elements that we will receive linear algebraic system concerning variables
which solutions have the form:
Therefore, if the original antiquaternion
We will define some properties of conjugate antiquaternions. 1) the sum and the product of conjugate antiquaternions is a real numbers; 2)the conjugate of the sum is the sum of conjugated 3) the conjugate of the product is the product of conjugated
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 118; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.70.99 (0.006 с.) |

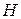 with basis
with basis 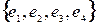 the multiplication table of elements which is;
the multiplication table of elements which is;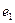
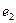
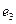
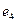
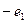
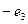
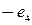
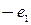
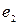
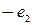
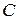 by same system of numbers. Or, using a system of markings, introduced in [3], we can write:
by same system of numbers. Or, using a system of markings, introduced in [3], we can write: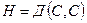 . (1)
. (1)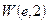 with multiplication table
with multiplication table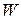
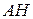 , or through operator of doubling:
, or through operator of doubling: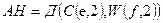 . (2)
. (2)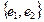 and
and 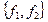 , we obtain a basis
, we obtain a basis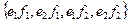 .
.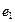 or
or 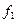 . Basic elements
. Basic elements 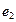 and
and 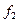 are multiplied anticommutatative.
are multiplied anticommutatative.
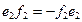 .
.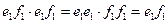
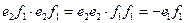
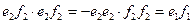 .
. ,
, 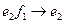 ,
, 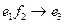 ,
, 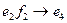 ,
,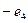
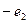
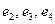 of antiquaternion’s system are represented by triangle tops. Product of any two elements from this three is equal to the third if movement from the first to the second multiplier coincides with the arrow direction, if the movement is opposite to the direction of the arrow - the third with a minus sign.
of antiquaternion’s system are represented by triangle tops. Product of any two elements from this three is equal to the third if movement from the first to the second multiplier coincides with the arrow direction, if the movement is opposite to the direction of the arrow - the third with a minus sign.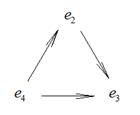
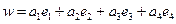 , (4)
, (4)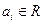 .
. :
: 
 and
and  .
. (5)
(5) ;
; ;
;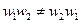 . (6)
. (6) ,
,
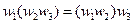 .
. ;
;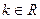 ,
, ;
; is performed
is performed  .
. , (7)
, (7) - structural constants of hypercomplex numerical system of antiquaternions
- structural constants of hypercomplex numerical system of antiquaternions 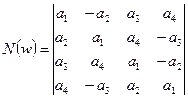 . (8)
. (8) :
: (9)
(9)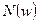 :
: . (10)
. (10) . (11)
. (11) (12)
(12) , (13)
, (13) :
: , (14)
, (14) . (15)
. (15)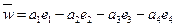 . (16)
. (16) ;
; , which can be verified directly.
, which can be verified directly.


