
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение среднемноголетнего расхода воды и модульных коэффициентовСодержание книги
Поиск на нашем сайте
Находят сумму значений расходов всех n членов убывающего ряда
Определяют первый параметр данного ряда – его среднее значение за многолетний период
Выражают значения всех параметров убывающего ряда в модульных коэффициентах (в долях среднего значения) Ki и записывают в гр.6:
Для контроля вычислений находят сумму значений
Проверка однородности ряда наблюдений Выявляют, нет ли в составе данного ряда нерепрезентативных (резко отклоняющихся) членов вследствие естественных обстоятельств, не характерных для периода наблюдений заданной продолжительности, или вследствие каких-то грубых ошибок. Для этого используют непараметрический критерий Диксона. Находят его значения для крайних членов выборки – наибольшего и наименьшего
Рисунок 1.1 – Многолетний гидрограф годового стока реки
где K1, K3 – значения модульных коэффициентов первого и третьего членов статистического ряда; Kn, Kn-2 – значения модульных коэффициентов последнего и третьего снизу членов ряда. Для n=30
Если оба или одно из вычисленных значений по формулам (1.3а) и (1.4а) окажутся больше 0,457 (критериального значения 1%-й значимости при n=30), то гипотеза об однородности членов ряда отвергается. Если они окажутся меньше 0,457, но больше 0,366 (критериального значения 5%-й значимости), то гипотеза сомнительна. Если же вычисленные значения меньше 0,366, то гипотеза принимается. В случае отклонения гипотезы, из ряда исключают проверяемый член. Проверяют на однородность ряд из оставшихся членов и при положительном исходе включают их в дальнейшую обработку.
Построение эмпирической кривой обеспеченности Ординатами точек эмпирической кривой являются значения Ki всех членов ряда. Абсциссы определяют по выражению
где pi – обеспеченность рассматриваемого члена со значением Ki; mi – номер члена Ki в убывающем ряду; n – общее число членов ряда.
1 – точки эмпирической кривой 2 – аналитическая кривая Рисунок 1.2 – Кривая обеспеченности годового стока
По полученным данным (pi,Ki) наносят точки эмпирической кривой (рис.1.2). Необходимо визуально убедиться, что не осталось ли резко отклоняющихся точек, свидетельствующих о неоднородности соответствующих членов ряда. Повторяемость N расхода заданной обеспеченности (число лет N, в течение которых такой расход повторяется в среднем 1 раз) можно определять по формулам:
p<50% (многоводные годы) N=100/p (1.6) p>50% (маловодные годы) N=100/(100-p) (1.7)
Таблица 1.1 – Расчет координат эмпирической кривой обеспеченности годового стока реки и исходных данных для определения статистик l
Расчет и построение аналитической кривой обеспеченности Для построения аналитической кривой обеспеченности необходимо определить два остальных ее параметра: коэффициенты вариации Сv и асимметрии Cs. Коэффициент вариации характеризуется отношением среднего квадратичного отклонения ряда к его среднеарифметическому
По номограммам (приложение 6) определяют значения параметров Сv и Cs аналитической кривой обеспеченности трехпараметрического гамма-распределения. Пользуясь таблицами ординат кривых трехпрараметрического гамма-распределения (приложение 6) и прибегая при необходимости к интерполяции, выписывают (табл.1.2) координаты аналитической кривой pi,Ki по установленным в п.1.5. значениям коэффициента Cv и соотношения Cs/Cv. Эту кривую совмещают на одном графике с эмпирической кривой и визуально оценивают степень согласования (рис.1.2).
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 368; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.28.90 (0.008 с.) |

 и записывают ее внизу гр.4 табл.1.1.
и записывают ее внизу гр.4 табл.1.1. (1.1)
(1.1)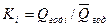 (1.2)
(1.2)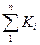 , которая должна быть равна числу членов ряда n.
, которая должна быть равна числу членов ряда n. (1.3)
(1.3) , (1.4)
, (1.4)



 (1.3а)
(1.3а) (1.4а)
(1.4а) , (1.5)
, (1.5)





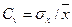 , а коэффициент асимметрии – отношением среднего значения отклонений в кубе (среднее кубическое отклонение) к среднему квадратическому в кубе
, а коэффициент асимметрии – отношением среднего значения отклонений в кубе (среднее кубическое отклонение) к среднему квадратическому в кубе  . Численные значения Сv и Сs могут определятся различными методами. В проекте используют метод наибольшего правдоподобия. Для этого вычисляют значения второй l2 и третьей l3 статистик
. Численные значения Сv и Сs могут определятся различными методами. В проекте используют метод наибольшего правдоподобия. Для этого вычисляют значения второй l2 и третьей l3 статистик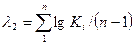 , (1.8)
, (1.8) . (1.9)
. (1.9)


