
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Часова характеристика лічильника.Содержание книги
Поиск на нашем сайте
Важливою характеристикою газорозрядних лічильників є МЕРТВИЙ ЧАС – це інтервал часу між початком імпульсу розряду і моментом, коли можливе виникнення наступного імпульсу розряду. Фізична причина існування мертвого часу полягає в тому, що на тлі потужного розряду, викликаного початковою частинкою, поява того чи іншого числа пара іонів зовні не позначається на характері процесів у лічильнику. Лавинна іонізація виникає поблизу дроту, де Е велике. Електрони, володіючи великою рухливістю, за час t=10-5з досягають анода. Іони, через велику їхню масу, рухаються до катода повільніше і утворять просторовий позитивний заряд, що оточує анод (рис.3.). Це на якийсь час зменшує напруженість електричного поля Е поблизу анода настільки, що ударна іонізація стає неможливою. Поступово позитивні іони ідуть від анода і напруженість електричного поля поблизу його зростає й у якийсь момент часу знову стає можлива іонізація і виникнення лавинного розряду. Зміна напруженості електричного поля Е у анода з моменту виникнення розряду показане на рис.4. (суцільна лінія 1). Пунктирна лінія 2 відповідає зміні напруженості електричного поля Е у анода при розвитку нового розряду. Лінія 3 відповідає граничному значенню Е. Звичайно мертвий час tМ=10-5с. Однак час, необхідне для повного відновлення працездатності лічильника tВ значно більше мертвого часу. Воно визначається швидкістю руху іонів і дорівнює тому часу, що затратять іони на проходження шляху від анода до катода. Якщо установка, що реєструє імпульси в лічильнику, досить чутлива, то відновлення працездатності лічильника визначається мертвим часом tМ..
Рис. 4
Роботу радіометричної установки (лічильник і реєструючий пристрій) характеризують роздільною здатністю або роздільним часом tроз. Роздільний час - це той мінімальний проміжок часу, яким повинні бути розділені прольоти ядерних часток для того, щоб можна було зареєструвати їх окремо. У загальному випадку цей час визначається мертвим часом tМ, часом відновлення tв, і чутливістю перерахункової установки. Тому що чутливість перерахункових пристроїв звичайно висока, те ядерні частки, що потрапили в лічильник під час його відновлення, будуть зареєстровані, що тому дозволяє час визначається МЕРТВИМ ЧАСОМ лічильника.
ЛІЧИЛЬНА ХАРАКТЕРИСТИКА ЛІЧИЛЬНИКА. Лічильна характеристика n(V) відбиває число імпульсів зареєстрованих установкою в залежності від напруги на електродах лічильника (рис.5.). Крива починає рости з деякого значення напруги V0. При напругах менших V0 амплітуда вихідних імпульсів лічильника недостатня для запуску рахункового пристрою.
Рис.5 В міру росту напруги V амплітуди імпульсів наростають, що і приводить до росту швидкості лічби. В області напруг від V0 до V1 має місце розкид імпульсів по амплітудах, що виникає унаслідок флуктуацій у розвитку і гасінні розряду і деяка частка імпульсів може виявитися не поліченою! При деякій напрузі V більшому V1 установка фіксує всі імпульси, що потрапили в лічильник. При подальшому підвищенні напруги швидкість рахунка не повинна змінюватися, однак досвід показує, що вона повільно підвищується. Це підвищення порозумівається появою так званих помилкових імпульсів, що виникають за рахунок порушення механізму гасіння розряду. Якщо продовжувати збільшувати напруга на лічильнику, то при деякім його значенні число помилкових імпульсів швидко зросте й у лічильнику виникає безупинний розряд, що не піддається гасінню. ВИКОНАННЯ РОБОТИ. а) Зняття рахункової характеристики: Для зняття рахункової характеристики лічильника зібрана схема, показана на мал.6. Після включення в мережу вся установка повинна нагрітися протягом 10 хв. Блок живлення (УІП) дозволяє змінювати напруги на лічильнику в межах V = 0-700 В. Для одержання точок графіка рахункової характеристики рекомендуємо змінювати напругу через 20 В, а час підрахунку імпульсів t=30 с. На графіку відкладаємо число імпульсів, зареєстрованих лічильником за 1с, тобто n = N/t, де: n – швидкість рахунка; N – число імпульсів за час t. Рис.6. Блок-схема установки: УІП - блок живлення; ВР - 7 - вольтметр; ПСО2 - 4 - перерахунковий пристрій; СГМ - лічильник Г.-М.; А - радіоактивний елемент. Результати досвідів заносять у таблицю:
Для оцінки статистичної помилки необхідно провести ряд вимірів (не менш 3-х) числа імпульсів N для середини плато кривої n(V) за час –100с і оцінити середній і відносний розкид швидкості рахунка Dnср і Dnср/nср (у процесі виміру не можна зміщати радіоактивний препарат, тому що це може привести до додаткових помилок виміру). За отриманим значенням N(V) необхідно побудувати графік n(V), визначити ширину плато графіка DV=V2-V1 і його нахил j, що обчислюється по формулі:
де Dn – зміна n по всій ширині плато. Лічильник вважається гарним, якщо ширина плато DV=250-300 В, а нахил j =3-5 %, мертвий час t = 10-4с. До характеристик лічильника відноситься робоча напруга Vp і V0. б) Визначення часу рахункової установки, що tдозволяє, р. (У роботі приймається, що tP = tM) Існує кілька методів виміру tM. У роботі використовується метод двох джерел. Для цей лічильник опромінюється потоком часток 1-го джерела - n1, потім потоком часток другого джерела - n2, а потім обома джерелами одночасно n1,2. Якщо tМ = 0, то лічильник зареєструє показання так, що n1,2 = n1 + n2. Якщо tМ № 0 (тобто при наявності прорахунків), n1,2 № n1 + n2 (звичайно tМ № 0, тому n1,2 < n1 + n2). Щоб знайти tМ використовуємо рівність виду:
Лічильник вважається гарним, якщо його tМ= 1-2Ч 10-4с. РЕЗУЛЬТАТИ РОБОТИ. 1. Представити графік n(V) із указівкою потрібних крапок і величин, що визначаються; 2. Визначити tр, порівняти з паспортними даними; 3. Записати тип лічильника, його паспортні дані й отримані характеристики лічильника з указівкою можливої помилки виміру: V0, Vраб, ДV, ц, ф. КОНТРОЛЬНІ ПИТАННЯ. 1. Як улаштований лічильник Гейгера-Мюллера? Яке його призначення? 2. Які фізичні процеси дозволяють фіксувати частки, що попадають у лічильник? 3. Описати рахункову характеристику лічильника? 4. Чим визначається час рахункової установки, що дозволяє? 5. Як оцінити мертвий час лічильника?
ЛІТЕРАТУРА. 1. Савельєв И.В. Курс загальної фізики. т.3. 1973,1979.; 2. Садеков Х.М. Експериментальне дослідження деяких властивостей ядерного випромінювання. Уфо,1980.; 3. Сивухин. Курс загальної фізики. т.4.
ДОСЛІДНІ РЕЗУЛЬТАТИ
Графік: лічильна характеристика лічильника.
Дані для визначення мертвого часу.
Характеристики лічильника 1. Визначені дослідом.
Лабораторна робота № 2 ВИВЧЕННЯ ЗАКОНОМІРНОСТЕЙ РАДІОАКТИВНОГО РОЗПАДУ МЕТА РОБОТИ: визначити характер закономірності радіоактивного розпаду. ЗАВДАННЯ: 1. Отримати статистичні дані, що характеризують розпад ядер у радіоактивному препараті; 2. Порівняти отримані статистичні дані розпаду ядер з теоретичною кривою, яка характеризує статистичний процес; 3. Визначити характер закономірності радіоактивного розпаду. ТЕОРЕТИЧНІ ВІДОМОСТІ. Розділяють два типи фізичних закономірностей: динамічні і статистичні. Динамічні закономірності дають однозначну картину явищ, тобто знаючи умови, що характеризують систему в деякий початковий момент часу, можна передбачити її стан в будь-який момент часу. Статистичні закономірності встановлюють зв'язок між явищами, які не носять однозначний характер. Ці закономірності проявляють себе тоді, коли випадкові явища протікають незалежно одне від одного. При дослідженні статистичних закономірностей важливу роль має статистична похибка. Вона пояснюється наявністю флуктуацій у вимірюваній величини біля її середнього значення. Радіоактивний розпад ядер носить імовірний характер. При цьому імовірність розпаду ядра Р пропорційна інтервалу часу Dt і може бути представлена у вигляді:
де l - постійна розпаду, що визначається властивостями ядра. Завдяки спонтанного розпаду ядер закон радіоактивного розпаду має вигляд:
No – число радіоактивних ядер в момент часу t = 0; N(t) – число радіоактивних ядер в момент часу t. Закон радіоактивного розпаду носить статистичний характер і виконується точно тільки для великих чисел No і N. Статистичний характер закону можна перевірити експериментально за методикою, запропонованою Резерфордом і Гейгером. Вони підраховували число частинок, які випромінював радіоактивний препарат малої інтенсивності за однакові проміжки часу. Далі за результатами експерименту визначалась загальна кількість періодів (проміжків) часу, за який випромінювалось однакове число частинок і будувався графік залежності числа інтервалів N від числа зареєстрованих часток n, тобто Nек(n).Отримана під час експерименту залежність Nек(n) порівнювалась з аналогічною теоретичною залежністю, описаною статистичною формулою Пуассона. Формула Пуассона описує статистичні процеси, що носять дискретний і незалежний характер. З її допомогою можна передбачити імовірність Р(ni) певної події (поява ni частинок за проміжок часу Dt=1 с). Формула Пуассона має вигляд:
де
де, ni – число імпульсів за i -й проміжок часу, “ i ” змінюється від 1 до К, де К – кількість інтервалів (проміжків часу) в досліді. Користуючись формулою (2) можна розрахувати теоретично скільки разів при виконанні досліду спостерігається однакове число імпульсів NТ(ni) радіоактивного розпаду. Якщо всіх інтервалів в досліді було К, то: N(ni)=P(ni)•K (4) Порівнюючи графік Nек(ni), що отримали експериментально, із графіком NT(ni) можна визначити їх подібність чи розбіжність і зробити висновок про характер закону радіоактивного розпаду. Якщо графіки збігаються в межах можливих похибок, то закон радіоактивного розпаду носить статистичний характер і імовірність певного розпаду можна визначити за формулою Пуассона (2). В цьому переконуються студенти, виконуючи дану лабораторну роботу.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 386; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.236.93 (0.007 с.) |




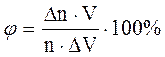 (2)
(2) (3)
(3)

 ,
,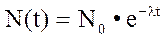 (1)
(1) (2)
(2) – середнє число частинок, що з’являються за проміжок часу Dt=1 с.
– середнє число частинок, що з’являються за проміжок часу Dt=1 с.  (3)
(3)


