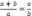Концепции симметрии и асимметрии. Природные проявления симметрии.

Понятие о взаимосвязи и размерности физических величин.

Все явления в мире так или иначе взаимосвязаны и подчиняются общим физическим законам. Чтобы иметь возможность сопоставлять физические величины друг с другом, производить расчеты нужно каждую физическую величину представить через некоторые общие для всех исходные физические величины, принимаемые за первичные. Однако эти первичные величины могут быть выбраны произвольно, и тогда при определении их физической сущности и при расиста” неизбежно возникнут дополнительные трудности. Чтобы их избежать, нужно определить те физические категории, которые являются неизменными при преобразованиях материи при взаимодействии материальных образований, (относительно которых будут оцениваться все остальные физические величины и параметры. Но если речь идет о всеобщих закономерностях материи во Вселенной, то должны быть определены всеобщие физические инварианты, которые не изменяются ни при каких преобразованиях форм материи и ни при каких физических процессах. То есть они инвариантны по отношению и к преобразованиям форм материи, и к конкретным физическим явлениям.

Общими физическими инвариантами могут быть только такие категории, которые являются всеобщими для всех без исключения физических явлений, то есть для всей реальности нашего физического мира. Такими категориями является движение и три его неразрывных составляющих — материя, пространство и время. Ибо в мире нет ничего, кроме движущейся материи. И следовательно, все физические величины и все физические явления так или иначе будут определяться этими категориями как исходными. Именно они поэтому и должны валяться основой любой системы измерений, т.е. в основе любой системы измерений должны являться три величины — мера материя, такой мерой является единица массы как количества материи и обозначается через символ М (от англ. слова "matter" — вещество, материя); мера пространства, такой мерой является единица длины и обозначается через символ L (от англ. слова "length" — длина); мера времени, такой мерой является единица времени и обозначается через символ Т (от англ. слова “time” — время).

Размерность физической величины — это выражение, показывающее связь данной физической величины с физическими величинами, положенными в основу системы единиц. Размерность записывается в виде произведения символов соответствующих основных величин, возведенных в определенные степени, которые называются показателями размерности. Величины, в которые все основные величины входят в степени 0, называются безразмерными. Во всех остальных случаях размерность конкретной физической величины записывается в виде:

[u]=M^xL^yT^z,

— есть обозначение самой величины, х, у, z — показатели размерности каждой из основных величин. Например, размерность ускорения должна быть записана в виде:uгде

[a] = LT^-2,

а размерность работы и мощности соответственно в виде:

[А] = МL² T^-2, [Р = МL² T^-3.

Поскольку во многих случаях такой вид обозначений не очень удобен, то на практике применяются производные величины, изначально содержащие в себе исходные величины в определенных степенях. Таким величинами являются, например, мера площади — м², мера объема — м³, мера силы — Ньютон (Н), равная [Н] = МLT^-2 или Н = кг*м*с^-2 или мера работы — Джоуль (Дж), равная [Дж] = МL²Т^-2 или Дж = кг ×м²×с^-2 , и т.п.

Сущность процесса измерений. Погрешности измерений, их виды, причины возникновения.

Всякое измерение неизбежно связано с погрешностями.

Погрешность измерений — разность между полученным при измерении X' и истинным 0 значениями измеряемой величины. Погрешность измерения определяется формулой:

∆ = X' - Q.

Погрешность измерений вызывается несовершенством методов и средств измерений, непостоянством условий наблюдения, а также недостаточным опытом наблюдателя или особенностями его органов чувств.

Погрешности, связанные с несовершенством метода измерения, называют методическими. Эти погрешности вызваны неучетом в использованном методе измерений многих факторов, так или иначе искажающих измеряемую величину. Поскольку таких факторов бесчисленное множество, то в методике измерений должны быть учтены те, которые оказываются существенными для задачи, для которой производится измерение. Например, при измерении высоты с помощью барометрического высотомера оказывается необходимым учитывать изменение давления на земле при посадке самолета, но этого не нужно делать при занятии заданного эшелона, поскольку для всех самолетов эта ошибка одна и та же.

Погрешности, связанные с несовершенством инструмента измерения, называют инструментальными.

Погрешности измерений могут быть абсолютными, относительными или приведенными.

Абсолютными погрешностями являются погрешности, выраженные в единицах измеряемой величины; относительными — выраженные либо в процентах от нее, либо в процентах от верхнего предела измерений (диапазона); приведенные — в процентах от длины шкалы.

Погрешности, имеющие место при нормальных условиях применения прибора, называются основными, погрешности, вызванные отклонениями влияющих величин от нормальных, называются дополнительными.

При измерении достоянных величин погрешности являются статическими, при измерении изменяющихся во времени величин к ним добавляются динамические составляющие погрешности.

Погрешность в системах автоматического регулирования — разность между заданным и действительным значениями регулируемой величины в процессе регулирования. Погрешность в любой момент времени можно рассматривать как сумму погрешности в установившемся режиме (статическая) и погрешности в переходном процессе (динамическая). При статистическом анализе качество работы САР оценивают по критериям, связанным с вероятностными характеристиками погрешностей, например, по минимуму среднеквадратичной ошибки.

Структура измерительных устройств.

Измерительное устройство — средство измерений, предназначенное для выработки сигнала измерительной информации в форме, удобной для передачи, преобразования и (или) использования в автоматических системах управления.

Измерительные приборы — средства измерений, дающие возможность непосредственно отсчитывать значения измеряемой величины. В аналоговых измерительных приборах отсчитывание производится по шкале, в цифровых — по цифровому отсчетному устройству. Показывающие измерительные приборы предназначены только для визуального отсчитывания, регистрирующие снабжены устройством записи: на бумаге, на магнитной ленте или в электронной памяти.

Общую структуру измерительных устройств можно представить в виде последовательного соединения: первичного преобразователя, вторичного преобразователя и индикаторного (регистрирующего) устройства. В качестве индикаторных устройств в современных измерительных приборах используют цифровые индикаторы, а в качестве регистрирующих - устройства с электронной цифровой памятью.

(если покажется мало, можно списать что-то из пункта 11, но это на любителя)

Фотоэлементы

I - устройство вакуумного фотоэлемента

Применение:

· Кино: воспроизведение звука

· Фототелеграф.

· Фотометрия: для измерения силы света, яркости, освещенности.

· Управление производственными процессами.

II внутренний фотоэффект используется в фоторезисторах

Фоторезистор – устройство, сопротивление которого зависит от освещенности.

Механизм внутреннего фотоэффекта. При попадании излучения внутрь вещества происходят два явления. Одни кванты излучения, поглощаясь атомами (или ионами), увеличивают кинетическую энергию их теплового движения, поэтому вещество нагревается. Другие кванты излучения, поглощаясь атомами, производят фотоионизацию, в результате чего в веществе образуются дополнительные носители заряда – электроны проводимости и дырки. Их образование ведет к уменьшению электрического сопротивления.

Используется при автоматическом управлении электрическими цепями с помощью световых сигналов и в цепях переменного тока.

III. Вентильный фотоэффект

Полупроводниковый фотогальванический элемент – прибор, в котором образуется электродвижущая сила в электрическом переходе между разнородными полупроводниками при действии на него электромагнитного излучения.

При поглощении кванта излучения электронным полупроводником освобождается дополнительная пара носителей заряда – электрон проводимости и дырка, которые движутся в разных направлениях: генерируемая дырка движется в сторону дырочного полупроводника, а генерируемый электрон проводимости – в сторону электронного полупроводника. В результате образуется избыток электронов проводимости в одном полупроводнике и избыток дырок в другом. Так на электродах фотоэлемента создается фотоэлектродвижущая сила.

Используется в солнечных батареях, которые имеют КПД 12-16% и применяются в искусственных спутниках Земли, при получении энергии в пустыне.

Отличие живого от неживого.

Все вещество на планете разделяется на живое и неживое вещество. И хотя, казалось бы, нет никаких проблем в том, чтобы отличить одно от другого, на самом деле никто не знает точно, где находится переход от неживого к живому.

Вернадский определяет живое вещество как совокупность живых организмов в биосфере.

· Живое вещество обладает намного меньшей совокупной массой в отличие от неживого вещества (2,4-3,6×1012 т, что составляет меньше чем одну миллионную от массы других оболочек нашей планеты). В то же время живое вещество играет очень важную роль в биосфере.

· Ареал существования живого вещества ограничен участком на пересечении атмосферы, гидросферы и литосферы.

· В живом веществе значительно быстрее протекают химические реакции в отличие от химических реакций в неживом веществе (разница может быть в тысячи или миллионы раз)

· Живое вещество обладает значительно большей свободной энергией, чем неживое вещество.

· Живому веществу присуща смена поколений при наличии эволюции (то есть каждое следующее поколение обладает рядом новых признаков)

· Живое вещество имеет значительно большее химическое и морфологическое разнообразие. Оно не бывает представлено только жидкой или газообразной формой – организмы построены во всех трех состояниях. Человеку известны более 2 миллионов органических соединений, из которых состоит живое вещество, в то время как неживое вещество состоит из около 2 тысяч соединений.

· Составляющие живого вещества устойчивы только в живых организмах

· Живое вещество существует в виде индивидуальных организмов, размеры которых могут очень сильно различаться. Так, например, размеры вирусов не превышают 20 нм (1 нм = 10-9м), великаны животного мира киты вырастают не больше 33 м в длину, а а такие гигантские растения, такие как секвойа, могут быть больше 100 м в высоту (абсолютный рекорд – секвойа «Гиперион», высота 115.5 метров.

· Живому существу в значительной степени присуще саморегулируемое движение.

Белки. Строение и функцию.

Из органических веществ, входящих в живую клетку, важнейшую роль играют белки. На их долю приходится около 50% массы клетки. Благодаря белкам организм приобрел возможность двигаться, размножаться, расти, усваивать пищу, реагировать на внешние воздействия и т. д.

Белки – это сложные высокомолекулярные природные соединения, построенные из аминокислот. В состав белков входит 20 различных аминокислот, отсюда следует огромное многообразие белков при различных комбинациях аминокислот.

В организме человека насчитывается до 100 000 белков.

Белки подразделяют на протеины (простые белки) и протеиды (сложные белки).

Первичная структура белка – последовательность чередования аминокислотных остатков (все связи ковалентные, прочные).

Вторичная структура – форма полипептидной цепи в пространстве. Белковая цепь закручена в спираль (за счет множества водородных связей).

Третичная структура – реальная трехмерная конфигурация, которую принимает в пространстве закрученная спираль (за счет гидрофобных связей), у некоторых белков – S–S-связи (бисульфидные связи).

Четвертичная структура – соединенные друг с другом макромолекулы белков образуют комплекс.

Функции белков:

1. Строительный материал – белки участвуют в образовании оболочки клетки, органоидов и мембран клетки. Из белков построены кровеносные сосуды, сухожилия, волосы.

2. Каталитическая роль – все клеточные катализаторы – белки (активные центры фермента). Структура активного центра фермента и структура субстрата точно соответствуют друг другу, как ключ и замок.

3. Двигательная функция – сократительные белки вызывают всякое движение.

4. Транспортная функция – белок крови гемоглобин присоединяет кислород и разносит его по всем тканям.

5. Защитная роль – выработка белковых тел и антител для обезвреживания чужеродных веществ.

6. Энергетическая функция – 1 г белка эквивалентен 17,6 кДж.

Концепции симметрии и асимметрии. Природные проявления симметрии.

Симметрия (от греч. symmetria— соразмерность) свойство геометрической фигуры, характеризующее некоторую правильность формы, неизменность ее при тех или иных видах отражений.

В узком смысле симметрия относительно плоскости (зеркальное отражение) — такое преобразование в пространстве (относительно прямой на плоскости), при котором каждой точке фигуры, расположенной на некотором расстоянии от плоскости симметрии, соответствует аналогичная точка той же фигуры, расположенная на таком же расстоянии от плоскости симметрии по другую ее сторону. Симметрия — соразмерность, зеркальное отражение относительно плоскости. Асимметрия — отсутствие симметрии.

Различают центральную симметрию, при которой фигура совмещается сама с собой после последовательного отражения от трех взаимно перпендикулярных плоскостей; осевую симметрию, при которой фигура накладывается сама на себя вращением вокруг некоторой прямой на угол 360/n градусов; зеркально-осевую симметрию, при которой фигура накладывается сама на себя вращением вокруг некоторой прямой на угол 360/n градусов и отражением в плоскости; симметрию переноса, при которой фигура совмещается сама с собой после переноса вдоль некоторой прямой. Существуют еще симметрии относительно оси, относительно точки и пр.

Симметрия широко распространена в природе, особенно в кристаллах и в биологии, широко используется в искусстве и в архитектуре.

В физике предполагается, что раз пространство изотропное, то все явления должны иметь в природе свое зеркальное отражение, т. е. иметь симметричное состояние. Симметричных тел много, например, почти все живые организмы, многие кристаллы и пр.

На самом деле в природе симметрия наблюдается далеко не во всех процессах и явлениях. Право и левовинтовое движения представлены неодинаково, если материя представлена в природе широко, то антиматерия практически вообще не представлена. Это объясняется прежде всего тем, что основной частицей микромира является протон, в котором винтовое движение имеет определенный знак, и однажды возникшее винтовое движение непрерывно порождает движение того же знака. Электроны имеют противоположный знак винтового движения, но их масса в 1850 раз меньше, чем протона. Поэтому хотя собственно пространство и симметрично, природа несимметрична.

Чтобы симметрия созданий природы не вступала в конфликт с симметрией сил земного тяготения, ось тела любых организмов, которые обречены всю жизнь стоять неподвижно, расти вертикально вверх, должна обязательно приобрести лучевую симметрию, организмы, передвигающиеся параллельно поверхности Земли должны иметь двустороннюю зеркальную симметрию.

Безусловно, симметрия живых организмов не абсолютна, например, расположение органов во многом не симметрично. Однако все, что касается органов движения — ног, крыльев симметрия выполняется достаточно строго.

Принципы симметрии в равной мере распространяются и на творение рук человека. Окружающие нас предметы чаще всего имеют радиальную или билатеральную (зеркальную) симметрию, и это придает им дополнительную надежность и простоту в обращении.

К своеобразной симметрии (асимметричной симметрии) относится “Золотое сечение” или “Божественная пропорция”. Золотым сечением (божественной пропорцией) называют такое деление отрезка на две части, при котором большая часть относится к меньшей как весь отрезок относится к большей части. Пифагор был первым, кто обратил внимание на замечательные свойства золотого сечения.

Пусть точка С делит отрезок АВ на две части а и b так, что отношение отрезков образует с длиной всей линии такую пропорцию:

Если обозначить отношение а/b= x, то уравнение перепишется в виде:

1+ или x² - x -1 =0

Отсюда находим:

X =

Приближенные значения корней таковы:

x1 =. 1,61803398875.... x2, = -0,61803398875...

В 1509 г., то есть примерно через две тысячи лет после Пифагора, итальянец Фра Лука Пачиоли (1445-1509) опубликовал книгу “О божественной пропорции”. Рисунки к этой книге выполнил знаменитый друг Пачиоли Леонардо да Винчи. Ему же, кстати, принадлежит и термин “Золотое сечение”. Рассмотрим некоторые свойства этой удивительной пропорции.

и е. О нем после Пифагора писали Платон, Поликлет, Евклид, Витрувий и многие другие. В новое время золотым сечение интересовались многие именитые художники, скульпторы, архитекторы. Вызвано это тем, что всюду, где присутствует “золотое” число Ф, живые формы и произведения архитектуры приятны для глаз, отличаются явной гармоничностью и красотой.pОбозначим х1 = Ф. Тогда х2 = -Ф-1. Пачиоли доказал, что последовательность чисел вида Ф-1, Ф0, Ф1, Ф2... является геометрической прогрессией.. Число Ф не менее замечательно, чем числа

Золотое сечение можно встретить в пропорциях человеческого тела и в расположении листьев на ветках. Присмотритесь к деревьям — между двумя парами листьев третий лист находится в точке золотого сечения. Длина главной балки (архитрава) знаменитого Парфенона относится к высоте здания, как 1/0,618. Подобные соотношения давно найдены в таких шедеврах архитектуры, как церковь на Нерли или храм Вознесения в Коломенском. В музыке также есть следы вездесущего золотого сечения. Так благозвучные интервалы и аккорды (консонансы) имеют соотношение частот близкое к Ф. Кульминация мелодии часто приходится на точку золотого сечения ее обшей продолжительности.

Пулковский астроном К. П. Бутусов обнаружил, что соотношение периодов обращений соседних планет равно числу Ф или Ф2. По его данным частоты обращений планет и разности частот обращений образуют спектр с интервалом, равным Ф, то есть спектр, построенный на основе золотого Сечения. Вот она гармония небесных сфер о которой знали или которую предполагали еще пифагорейцы. Любопытно, что расположение перигелиев и афелиев планет по логарифмическим спиралям, как доказал К. П. Бутусов, также связано с “гармоническими” числами Ф. Примечательна связь живого с золотым числом, поэтому планетные и космические образования тоже могут быть своеобразными проявлениями живого.