
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическое обоснование рационализации методов учётовСодержание книги
Поиск на нашем сайте
В ранее опубликованных работах, посвящённых сосущим вредителям яблони, характер распределения изучаемых показателей не указывается. В наших исследованиях мы обратили внимание на то, что коэффициенты асимметрии и эксцесса подавляющего большинства выборок, особенно, при низкой плотности популяции вредителей, были существенно выше нуля, а коэффициенты вариации достигали 70 – 150% и более. Данный факт свидетельствует о несовместимости эмпирического распределения с нормальным распределением. По сравнению с законом нормального распределения для распределения численности сосущих вредителей яблони и большинства биометрических показателей характерна более высокая вероятность появления низких значений отклонений в интервале от –1 до 0σ (значения меньше среднего арифметического составляли от 55 до 90 % значений). Также возрастает вероятность аномально высоких отклонений (более +2σ). Из рассмотренных нами теоретических распределений (нормальное, логнормальное, гамма, экспоненциальное, Пуассона, Вейбулла, двойное экспоненциальное) наилучшее соответствие с опытными данными показало гамма-распределение с параметрами В формате Microsoft Excel: альфа (параметр формы): =СРЗНАЧ(данные)^2/ДИСП(данные) бета (параметр масштаба): =ДИСП(данные)/СРЗНАЧ(данные) (1) Общепринятым методом определения доверительных интервалов является расчёт по распределению Стьюдента. В рассматриваемых нами случаях он даёт близкие к реальности доверительные границы лишь при объёме выборки 20 и более единиц (см. таблицу 5). При меньшем объёме выборки доверительные границы необоснованно расширяются, что снижает точность исследования, при очень малом объёме выборки возможен даже выход нижней доверительной границы средней численности в область отрицательных значений (!), что является невозможным, поскольку изучаемые показатели не могут быть отрицательными. Проведённый машинный эксперимент показывает, что распределение выборочных оценок является асимметричным и асимметрия увеличивается с уменьшением объёма выборки. При этом медиана оценок меньше среднего значения, а интервал от верхней доверительной границы до среднего значения существенно шире, чем интервал от нижней доверительной границы до среднего значения. Расчёт доверительных интервалов с использованием гамма-распределения позволяет получить результат, значительно более близкий к реальному распределению выборочных оценок (таблица 5). Для вычисления доверительных границ используется формула: =ГАММАОБР(p;альфа*n;бета/n) (2) где p – перцентиль выборочных оценок (обычно 0,05 для нижней границы и 0,95 – для верхней границы); альфа и бета – параметры распределения, вычисляются по формуле (1); n – объём выборки.
Для совокупностей с более сильной асимметрией (при более высокой вариации, при более низкой численности) распределение выборочных оценок будет ещё сильнее отличаться от закона нормального распределения, поэтому для адекватного применения распределения Стьюдента потребуются выборки ещё большего объёма. Вычисление доверительных границ по формуле (2) позволяет правильно оценить погрешность даже при очень малом объёме выборки, при этом, бесспорно, с увеличением количества учётных единиц, точность выборочных оценок увеличивается. При асимметричном распределении в совокупности недостаточно знания только среднего арифметического значения, которое в данном случае не является типичным для совокупности. Наглядное представление о величине и распределении признака дают структурные параметры (квантили). В простейшем случае совокупность разделяется на 4 равные части: 1) с наименьшими значениями признака (от минимума до нижнего квартиля); 2) с пониженными значениями (от нижнего квартиля до медианы); 3) с повышенными значениями (от медианы до верхнего квартиля); 4) с наибольшими значениями (от верхнего квартиля до максимума). При более подробном анализе возможно деление совокупности на 10, 20 и более равных частей по децилям и перцентилям. Ошибки выборочных оценок медианы и перцентилей могут быть вычислены как ошибки доли, следовательно, при большом объёме выборки они нормально распределены (Смирнов, Дунин-Барковский, 1969). Формулы расчёта доверительных границ при n > 30 имеют вид: Для нижней границы: =ПЕРСЕНТИЛЬ(данные;P-СТЬЮДРАСПОБР(pa;n-1)*КОРЕНЬ(P*(1-P)/(n-1))) Ожидаемое значение: =ПЕРСЕНТИЛЬ(данные;P) Для верхней границы: =ПЕРСЕНТИЛЬ(данные;P+СТЬЮДРАСПОБР(pa;n-1)*КОРЕНЬ(P*(1-P)/(n-1))) (3) где: данные – диапазон ячеек выборки; pa – уровень значимости (обычно 0,05); P - искомый перцентиль (0,25 – нижний квартиль, 0,5 – медиана, 0,75 – верхний квартиль и т.д.). При n < 30 при гамма-распределении используются формулы: Ожидаемое значение: =ГАММАОБР(P;альфа;бета) Нижняя доверительная граница: =ГАММАОБР(P-СТЬЮДРАСПОБР(pa;n-1)*КОРЕНЬ(P*(1-P)/(n-1));альфа;бета) Верхняя доверительная граница: =ГАММАОБР(P+СТЬЮДРАСПОБР(pa;n-1)*КОРЕНЬ(P*(1-P)/(n-1));альфа;бета) (4) Таким образом, в случае гамма-распределения сравнение совокупностей при малых выборках по критерию Стьюдента нежелательно, так как при низких значениях параметра формы, выборочные распределения являются асимметричными. Сравнение лучше осуществлять по доверительным границам средних арифметических значений, вычисленным с использованием гамма-распределения. Если доверительные интервалы не перекрываются – значит, различия между вариантами существенны при использованном уровне значимости. Хорошие и наглядные результаты даёт также сравнение совокупностей по диаграммам децилей или квартилей (см. главу 7.3). Использование гамма-распределения и структурных параметров выборки позволяет более обоснованно подойти к интерпретации результатов исследований. Определение объёма выборки в зависимости от требуемой точности учёта до сих пор слабо обоснованно. Известная формула Нами накоплен обширный статистический материал, позволяющий установить необходимый объём выборки в зависимости от требуемой точности учёта (см. таблицы 2 и 4). В производственных ситуациях и в научных исследованиях, не требующих высокой точности, следует ориентироваться на ожидаемую погрешность в половине случаев (минимальное значение в таблицах), лишь в особо ответственных исследованиях – на перцентиль 0,975 (максимальное значение). Необходимая точность зависит также от уровня значений признака – при высокой численности желательна погрешность в пределах от 5 до 30 %, при умеренной – 20 – 40 %, при низкой численности – погрешность может быть больше 50 %. Для оценки структурных параметров объём выборки составляет от 10 – 35 для грубых учётов до 140 – 400 единиц для точных учётов. При снижении точности учёта существенно сокращаются затраты труда. С целью более экономного использования ресурсов и получения более оперативной информации допустимо увеличение погрешности учётов, которое может сочетаться с повышением уровня значимости оценок до 0,1 – 0,25. Кроме того, объём выборки лимитируется допустимым ущербом для дерева при проведении учётов. Так, с одной взрослой яблони можно взять не более 2 – 5 погонных метров ветвей, 20 – 40 розеток и 100 – 500 листьев (1 – 2 % от количества на дереве), выборки большего объёма могут существенно повлиять на продуктивность. Поэтому, погрешности учётов на модельных деревьях составляют обычно от 12 до 30 % при высоком и от 20 до 90 % при низком уровне значений изучаемого признака. На величину ошибки опыта наибольшее влияние оказывают ошибки повторностей, меньшее – ошибки выборки внутри повторности и ещё меньшее – ошибки параллельных анализов (Доспехов, 1985). Отсюда следует, что наиболее выгодный метод учёта – по 1 учётной единице с каждого учётного дерева. Очевидно также, что при высокой численности достаточно оценки по баллам или округлённого подсчёта. При проведённых нами учётах изучаемых показателей при среднем значении признака более 10, применение грубого подсчёта позволяло сократить затраты труда в 1,1 – 1,7 раз без существенного увеличения погрешности учёта. При среднем значении признака от 10 до 20 целесообразен подсчёт с округлением до 5; от 20 до 50 – до 10; от 50 до 100 – до 25 и т.д. Шаг округления (цена балла оценки) должен быть в 1,5 – 5 раз меньше средней численности. Далее рассмотрим методику взятия проб в саду для оценки численности сосущих вредителей яблони. Для этого необходимо изучить распределение вредителей в кроне дерева и по территории сада. На дереве мы рассмотрели зависимость численности яиц яблонной медяницы и красного плодового клеща от стороны света, густоты кроны, центральной или периферийной части кроны, высоты над уровнем почвы и расстояния от кончиков ветвей. Проведённое исследование показало наличие некоторых различий по всем изученным факторам, однако эти различия были слабыми и незначительными по сравнению с общим варьированием признака. Численность яиц медяницы на взрослых деревьях наиболее высока с северной стороны кроны (η2 = 1 %[1]), что, вероятно, связано с наиболее благоприятными условиями во время зимовки. Сила влияния других факторов была очень слабой (0,1 – 0,2 %). Различия абсолютных значений по изученным факторам не превышали 13%, лишь по фактору стороны света – до 30 %. Поэтому, при малых выборках в производственных ситуациях ими можно пренебречь и производить выборку «наугад» с единственным условием – примерно ¼ часть ветвей должна быть взята с северной стороны кроны. При объёме выборки более 20 единиц следует брать равное количество ветвей по сторонам света (при проекции кроны, близкой к кругу). В научных исследованиях при объёме выборки более 150 единиц желательно брать равное количество ветвей по сторонам света, из нижнего и верхнего ярусов, 75 % ветвей с периферии и 25 % - из центра кроны. В каждом из этих секторов кроны ветви для учёта выбираются случайным образом. В научных исследованиях, а также в небольших частных садах рекомендуется проводить учёты на каждом дереве, поскольку максимальные различия между деревьями в саду при учётах яиц медяницы достигали 2 – 3 раз при высокой плотности популяции и 5 - 80 раз – при низкой плотности популяции. В то же время средняя численность вредителей на отдельных участках сада площадью от 0,5 га в сходных условиях в промышленных садах различалась незначительно, не более чем в 1,3 – 2 раза, что сравнимо с погрешностями малых выборок. Поэтому в выровненных садах в производственных ситуациях необязательно охватывать осмотром всю территорию сада. На территории исследованных садов мы рассмотрели распределение вредителей по сортам; по рядам (крайние ряды и центральная часть сада); в зависимости от количества заложенных плодовых почек и микрорельефа сада (на вершине холма, на склонах и в низине, перепад высот 10 м, площадь сада 4 га). Численность яиц медяницы была выше на возвышенных участках сада в среднем на 30 – 40 %, чем на склоне и в низине (η2 = 0,9 %). Численность личинок, напротив, была выше в низине на 20% (η2 = 0,3 %), что, вероятно, связано с лучшей выживаемостью личинок при лучшей обеспеченности яблонь влагой весной. По рядам деревьев различий в количестве яиц не выявлено, но количество личинок меньше на крайних рядах деревьев на 17 % (η2 = 0,3 %), возможно из-за более высокой численности энтомофагов. Сила влияния сорта яблони составляет 5 % для яиц и личинок и 3 % для имаго. Различия по сортам достигают 3 раз для яиц и имаго и 9 раз для личинок. Наиболее сильно заселяются медяницей сорта, для которых характерно большое количество крупных бутонов (Антоновка 600-граммовая и Коричное полосатое). Сорта, для которых характерно большое количество мелких бутонов (Бефорест, Боровинка, Спартан) сильно заселяются медяницей, но выживаемость личинок на них понижена. Сорта с небольшим количеством крупных бутонов (Анис полосатый, Старкинг), наоборот, слабее заселяются, но характеризуются более высокой выживаемостью личинок. Сорта, для которых характерно относительно слабое цветение (Джонатан, Лавриково, Суйслепское), менее всего заселяются медяницей. На деревьях с большим количеством плодовых почек численность яиц выше в среднем на 38 % (η2 = 1,4 %), а личинок – на 27 % (η2 = 0,4 %), чем на деревьях с малым количеством плодовых почек. Однако использовать данный показатель при типическом отборе нецелесообразно из-за высокой трудоёмкости его определения. Численность личинок медяницы в цветковых розетках в среднем на 29 % превышает численность в листовых розетках. Поэтому, для получения репрезентативной выборки следует брать розетки случайным образом (т.е. по таблице случайных чисел или брать розетку, соседнюю с той, на которой случайно остановился взгляд). Распределение диапаузирующих яиц красного плодового клеща в годы невысокой численности существенно не отличалось от такового у яблонной медяницы. Численность яиц на взрослых деревьях также была наиболее высока с северной стороны кроны (η2 = 1,5%). Рекомендации по отбору проб такие же, как для учётов яиц медяницы. Различия в плотности популяции в зависимости от микрорельефа и расстояния от границы сада не доказаны (P0 = 0,14 – 0,40). Сила влияния сорта составляет 9 % для яиц и 2 % для подвижных особей, различия по сортам достигают 4 – 7 раз. Чёткой зависимости между заселением различных сортов и площадью листьев не выявлено. Пепин шафранный заселяется слабее других сортов, вероятно, из-за менее опушённых листьев мелкого размера. Наиболее сильно заселяемый сорт Анис полосатый отличается крупными сильноопушёнными листьями. Как известно, на сильно опушённых листьях клещи лучше удерживаются при ветреной погоде (Соколов, 1967). Для сортов Бефорест и Спартан, на которых отмечено больше зимующих яиц, характерно большее количество листьев в розетках (в среднем 6 – 9 шт. против 4 – 6 шт. на остальных сортах). Численность подвижных особей выше примерно в 1,6 раза на деревьях со слабым цветением, вероятно, из-за лучшего развития листьев на таких деревьях (η2 = 0,2%). Однако количество отложенных яиц не зависело от силы цветения (P0 = 0,75). Таким образом, в распределении сосущих вредителей яблони преобладают случайные и неизвестные нам факторы, которые обуславливают варьирование значений примерно на 90%. Из рассмотренных нами факторов наиболее сильное влияние оказывают особенности отдельных сортов. Внутри кроны дерева основные различия наблюдаются по сторонам света, плотность популяции и красного плодового клеща, и яблонной медяницы выше с северной стороны кроны. Предлагается использовать типическую (в ряде случаев) или механическую выборку учётных деревьев и случайную выборку 10-см ветвей и розеток на дереве с равным количеством проб по сторонам света. В садах, выровненных по сортовому составу и рельефу применение типической выборки (кроме стороны света) нецелесообразно. Лишь в точных научных исследованиях пропорциональный типический отбор по некоторым факторам (сектор кроны, сорта, рельеф сада в исследованиях яблонной медяницы) желателен во избежание появления систематических ошибок выборки.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 268; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.56.125 (0.008 с.) |

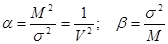 , вычисленными методом моментов.
, вычисленными методом моментов. имеет существенный недостаток – показатели вариации (дисперсия или коэффициент вариации) в совокупности, подлежащей изучению, нам неизвестны, их выборочная оценка может отличаться на различных деревьях в несколько раз, следовательно, объём выборки для определённой погрешности учёта может варьировать в 10 и более раз по результатам выборочных учётов. Кроме того, данная формула использует закон нормального распределения погрешностей, а как показано в таблице 5, при малых выборках распределение выборочных оценок асимметрично.
имеет существенный недостаток – показатели вариации (дисперсия или коэффициент вариации) в совокупности, подлежащей изучению, нам неизвестны, их выборочная оценка может отличаться на различных деревьях в несколько раз, следовательно, объём выборки для определённой погрешности учёта может варьировать в 10 и более раз по результатам выборочных учётов. Кроме того, данная формула использует закон нормального распределения погрешностей, а как показано в таблице 5, при малых выборках распределение выборочных оценок асимметрично.


