
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Graphical representation of electric field. Field lines and equipotential serfacesСодержание книги
Поиск на нашем сайте Graphically the electrostatic field represents with help of intensity vector’s lines, which are called field lines.
Field line is a type of line for which the tangent line to the path at each point is parallel to the vector of electric field intensity at that point. In order to also depict the magnitude, a selection of field lines is drawn such that the density of field lines (number of field lines per unit area) at any location is proportional to the magnitude of the vector of electric field intensity at that point. That's why in that place, where intensity is bigger, field lines situated more densely. The picture of field lines of point charges is shown on the Fig. 4. The field lines of positive charge start from the charge and finish in to infinity as a divergent rays, the field lines of negative charge start from the infinity and finish on the charge as a converging rays (Fig. 4). The fieldis homogeneous if in all its points intensity has the same magnitude and direction. The field lines of a homogeneous field are parallel among themselves. In a homogeneous field the distance between field lines equally. The field lines of electrostatic field aren’t intersected, are not closed.
In electrostatic field of any charge we can pick out such surface, in all points of which potentials are the same. Such surfaces are called equipotential, or surfaces of equal potential. From the formula (12) follows, that in the points, which are on the same distance from the point charge, potentials are the same. Hence, the fields' equipotential surfaces of the point charge are concentric spheres, centers of which coincide with position of the charge q (Fig. 5). Field lines of electrostatic field are always perpendicular to equipotential surfaces. It follows from the fact that the work of electrostatic field forces in the case of charge q ' moving between any two points of equipotential surface equals 0. A = q/ (j1 - j2) = 0, as j1 = j2 From the other side, dA=Fdl cos( As E ¹ 0 dl ¹ 0, so cos(
Relation between intensity and potential The work of electrostatic field force in the case of charge moving defines from the one side by the formula dA=q'Edr. From the other side as the decrease of potential energy dA= – dW = – q'd j. From the comparison of two formulas we get Edr= – d j; or
where dr – is the segment of the field line, which is perpendicucular to equipotential surface. Derivative of potential along the length of field line is called gradient of potential. Gradient of potential – is the vector directed towards the increase of potential. From the formula (15) follows:
Vector of intensity numerically equals gradient of potential and directed towards the decrease of potential. If the field is homogeneous, in any point of it E = const. For example, on the Fig. 6, is shown the field of infinite uniformly charged plate. Equipotential surfaces are the surfaces, parallel to the charged plate. Let's select in the field two equipotential surfaces with the potentials j1 and j2. It's evident, that j1 >j2. For homogeneous field relation between intensity and potential can be signed as
In the homogeneous field intensity numerically equals difference of potentials, which are on the unit of the field lines' length. From formulas (15) and (17) follows, that in the SI system intensity measures in V / m. If we build equipotential surfaces in such way, that the differences of potentials between any neighbouring surfaces were similar, so in the heterogeneous field these surfaces will unequal drop behind one from another. In places, where equipotential surfaces are closer to each other, the intensity of the field is greater.
|
|||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 198; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

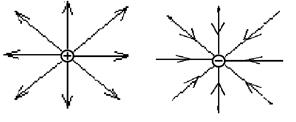 а) b)
Fig. 4–Field lines of positive (a) and negative (b) charges
а) b)
Fig. 4–Field lines of positive (a) and negative (b) charges
 а) b)
Рис. 5 – Equipotential lines of positive (a) and negative (b) charges
а) b)
Рис. 5 – Equipotential lines of positive (a) and negative (b) charges
 ,
,  ) =q/Edl cos(
) =q/Edl cos(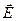 ,
,  ,
,  ) = 0, it means that
) = 0, it means that  . As vector of intensity is directed along the tangent to the field line, and dl lies on the equipotential surface, hence, field lines are perpendicular to the equipotential surface.
. As vector of intensity is directed along the tangent to the field line, and dl lies on the equipotential surface, hence, field lines are perpendicular to the equipotential surface. , (15)
, (15) (16)
(16) Fig. 6– Definition of electric intensity in point between the two equipotential lines
Fig. 6– Definition of electric intensity in point between the two equipotential lines
 (17)
(17)


