
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классическая и обобщенная модели множественной линейной регрессии. Условия применения метода наименьших квадратов, свойства его оценок.Стр 1 из 2Следующая ⇒
Классическая и обобщенная модели множественной линейной регрессии. Условия применения метода наименьших квадратов, свойства его оценок. Прогноз и оценка его точности на основе уравнений парной и множественной линейной регрессии. Нелинейные модели парной и множественной регрессии. Производственные функции. Системы эконометрических уравнений: виды, оценка параметров, области применения на практике. Экономическое моделирование основной тенденции развития временного ряда, взаимосвязей на основе данных временных рядов. Мультипликация и аддитивная модели временных рядов, прогнозирование на их основе.
Классическая и обобщенная модели множественной линейной регрессии. Условия применения метода наименьших квадратов, свойства его оценок. Несмещенные оценки означают, что математическое ожидание остатков равно нулю. Следовательно, при большом числе выборочных оценок коэффициента регрессии в найденный параметр по результатам одной выборки можно рассматривать как среднее значение из большого числа несмещенных оценок. Оценки считаются эффективными, если они характеризуются меньшей дисперсией (то есть мы имеем минимальную вариацию выборочных оценок). Оценки считаются состоятельными, если их точность увеличивается с увеличением объема выборки. Условия, необходимые для получения несмещенных, состоятельных и эффективных оценок, представляют собой предпосылки МНК, соблюдение которых желательно для получения достоверных результатов регрессии. Предпосылки МНК: 1- случайный характер остатков; 2- гомоскедастичность – дисперсия остатков одинакова для всех значений фактора; 3- отсутствие автокорреляции остатков (то есть остатки распределены независимо друг от друга); 4- остатки подчиняются нормальному закону распределения. Основная цель множественной регрессии - построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также их совокупное влияние на результативный признак. Для двухфакторной модели выборочное уравнение множественной линейной регрессии имеет вид: Для того, чтобы кроме состоятельности и несмещенности, оценки (обычного) МНК были ещё и эффективными (наилучшими в классе линейных несмещенных оценок) необходимо выполнение дополнительных свойств случайной ошибки:
Постоянная (одинаковая) дисперсия случайных ошибок во всех наблюдениях (отсутствие гетероскедастичности): Отсутствие корреляции (автокорреляции) случайных ошибок в разных наблюдениях между собой Данные предположения можно сформулировать для ковариационной матрицы вектора случайных ошибок Линейная модель, удовлетворяющая таким условиям, называется классической. Коренное отличие обобщенной модели от классической состоит только в виде ковариационной квадратной матрицы вектора возмущений: вместо матрицы Σε = σ2En для классической модели имеем матрицу Σε = Ω для обобщенной. Последняя имеет произвольные значения ковариаций и дисперсий. Например, ковариационные матрицы классической и обобщенной моделей для двух наблюдений (п=2) в общем случае будут иметь вид:
Найдем параметры модели методом наименьших квадратов, согласно которому:
где
n – число наблюдений Косвенный МНК Препятствие к применению метода наименьших квадратов, которое заключается в коррелированности эндогенных переменных со случайными членами легко преодолеть, если: 1) привести систему к виду, чтобы в правой части оставались только экзогенные переменные. Такая форма называется приведенной;
2) затем применить метод наименьших квадратов к каждому уравнению в приведенной форме и получить оценки ее параметров; 3) перейти от приведенной формы к структурной, проведя процедуру обратного преобразования параметров. Эта методика получила название косвенного метода наименьших квадратов и позволяет получать состоятельные и несмещенные оценки параметров структурной форму системы одновременных уравнений. Классическая и обобщенная модели множественной линейной регрессии. Условия применения метода наименьших квадратов, свойства его оценок.
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 534; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.190.232 (0.006 с.) |
 .
.




 .
. ;
; ,
, ;
; ;
; ;
; (
(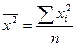 );
);


