
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расписание для преподавателя - Киршина И.А. - доц., к.т.н.
МАТЕРИАЛОВЕДЕНИЕ
Часть 2 Проводниковые материалы Лабораторный практикум
Санкт-Петербург 2013
УДК 621. 315. 416
Учебное пособие. Киршина И.А., Наймитенко Н.В., Плотянская М.А. Материаловедение. Часть 1. Проводниковые материалы. Лабораторный практикум/ СПбГУАП. СПб., 2013. 29 с.: 12 ил., 4 табл.
Учебное пособие подготовлено на кафедре микро- и нанотехнологии аэрокосмического приборостроения университета аэрокосмического приборостроения и предназначено для студентов специальностей, связанных с радиоаппаратостроением, приборостроением и электронной техникой, при изучении дисциплин “Материалы и элементы электронной техники”, “Материаловедение”, “Химия и материаловедение”, ”Материаловедение и ТКМ”, а также для выполнения лабораторных работ и самостоятельной подготовки.
Содержание
1 Проводниковые материалы 4 1.1 Физическая природа электропроводности металлов 4 1.2 Особенности кристаллической структуры металлов и сплавов 9 2 Температурная зависимость удельного сопротивления металлических проводников 11 3 Влияние примесей и других структурных дефектов на удельное сопротивление металлов 15 4 Влияние толщины металлических пленок на удельное поверхностное сопротивление 19 5 Физическая природа сверхпроводимости 20 Контрольные вопросы 22 6 Лабораторная работа №2. Исследование свойств проводящих сплавов 23 6.1 Порядок выполнения лабораторной работы №2а 26 6.2 Порядок выполнения лабораторной работы №2б 27 Литература 29
1 Проводниковые материалы
Проводники электрического тока могут быть твердыми телами, жидкостями, а при выполнении ряда условий и газами. Твердые проводники – металлы, сплавы и некоторые модификации углерода. По величине удельного сопротивления r металлические проводники делятся на следующие группы: – сверхпроводники; – криопроводники; – металлы и сплавы с высокой удельной проводимостью g; – металлы и сплавы со средним значением r; – металлы и сплавы с высоким значением r.
1.1 Физическая природа электропроводности металлов Металлические проводники – основной тип проводниковых материалов, применяемых в микроэлектронике. В классической электронной теории металлов – проводников I рода – электронный газ представлен свободными электронами. При учете лишь однократной ионизации выражение для концентрации свободных электронов n равно концентрации атомов:
где l – плотность металла; ma – атомная масса, NA=6,022045(31)×1023 моль-1 – число Авогардо, то есть число структурных элементов в единице количества вещества (в одном моле). К электронному газу применимы понятия и законы статистики обычных газов. Рассматривая хаотическое и направленное под действием силы электрического поля движение электронов, получено выражение закона Ома, закон Джоуля – Ленца. Плотность тока j в проводнике при средней скорости теплового движения электрона Vт, средней длине свободного пробега lср пропорциональна напряженности поля Е:
где m0 – масса электрона. Формула 2 – аналитическое выражение закона Ома при условии, что учтено движение одного электрона, а выводы распространены на все свободные электроны. Целесообразно учесть действие поля на всю совокупность электронов, когда суммарный импульс изменяется как при действии поля, и под действием соударений с узлами кристаллической решетки. Тогда средняя дрейфовая скорость электронов возрастает вдвое. С учетом этого выражение для удельной проводимости примет вид:
В качестве экспериментального факта установлено, что теплопроводность металлов пропорциональна их электропроводности. Представления о свободных электронах приводит к закону Видемана – Франца (1853г.), так как электрон в металле переносит не только электрический заряд, но и выравнивает в нем температуру за счет электронной теплопроводности. Отношение удельной теплопроводности λт к удельной проводимости g при комнатной и более высоких температурах T является постоянной величиной:
где Гипотеза об электронном газе в металлах подтверждается рядом опытов: - при длительном протекании тока через цепь, состоящую из одних металлических проводников, нет проникновения атомов одного металла в другой. - при нагревании металлов до высоких температур скорость теплового движения свободных электронов растет, они даже покидают металл, преодолев силы поверхностного потенциального барьера. - в момент остановки быстро двигавшегося проводника происходит смещение электронного газа по закону инерции в направлении движения. Появляется разность потенциалов на концах заторможенного проводника. - вследствие искривления траектории электронов в металлической пластине, помещенной в поперечное магнитное поле, появляется поперечная ЭДС и изменяется сопротивление проводника. Но есть и противоречащие факторы: – расхождения кривых в зависимости r(T) на опыте и теоретической; – наблюдаемая теплоемкость металлов ниже. Эти трудности удалось преодолеть с помощью квантовой волновой механики. Электронный газ в металлах при обычных температурах является "вырожденным". При этом средняя энергия электронного газа почти не меняется при изменении температуры. Основные недостатки классической теории исходят не столько из представлений о существовании в металлах свободных электронов, сколько от применения к ним законов статистики Максвелла – Больцмана, согласно которой распределение электронов по энергетическим состояниям описывается экспоненциальной функцией вида, когда в каждом энергетическом состоянии может находиться любое число электронов
Квантовая статистика базируется на принципе Паули, согласно которому в каждом энергетическом состоянии может находиться только один электрон. Отсюда сразу вытекает различие классического и квантового распределений электронов по энергиям. С классической точки зрения энергия всех электронов при температуре абсолютного нуля должна равняться нулю. А по принципу Паули даже при абсолютном нуле число электронов на каждом уровне не может превышать двух. И если общее число свободных электронов в кристалле равно n, то при ОК они займут n/2 наиболее низких энергетических уровней. В квантовой теории вероятность заполнения энергетических состояний электронами определяется функцией Ферми:
где W – энергия уровня, вероятность заполнения которого определяется; WF – энергия характеристического уровня, относительно которого кривая вероятности симметрична. При T = ОК функция Ферми обладает следующими свойствами: F(W) = 1, если W ≤ WF и F(W) = 0, если W > WF. Таким образом, величина WF определяет максимальное значение энергии, которую может иметь электрон в металле при температуре абсолютного нуля. Эту характеристическую энергию называют энергией Ферми или уровнем Ферми. Соответствующий ей потенциал φF = WF/e называют электрохимическим потенциалом. Следует отметить, что энергия WF не зависит от объема кристалла, а определяется только концентрацией свободных электронов, что непосредственно вытекает из принципа Паули. Поскольку концентрация свободных электронов в металле велика, энергия Ферми также оказывается высокой и в типичных случаях составляет 3 – 15 эВ. При нагревании кристалла ему сообщается тепловая энергия порядка kT. За счет этого возбуждения некоторые электроны, находящиеся вблизи уровня Ферми, начинают заполнять состояния с более высокой энергией: график функции распределения становится несколько пологим (рисунок 1). Однако избыток энергии, получаемой электронами за счет теплового движения, очень незначителен по сравнению с WF и составляет всего несколько сотых долей электрон-вольта. Поэтому характер распределения электронов по энергиям также изменяется очень незначительно: средняя энергия электронов практически остается без изменения. Незначительное изменение средней энергии от температуры означает малую теплоемкость электронного газа, значение которой по статистике Ферми – Дирака при обычных температурах получается в 50 – 70 раз меньше, чем по классической теории. В этом заключено разрешение противоречия между малой теплоемкостью и высокой проводимостью электронного газа в металлах. Из формулы (5) легко видеть, что при любой температуре для уровня с энергией W = WFвероятность заполнения электронами равна 0,5. Все уровни, расположенные ниже уровня Ферми, с вероятностью больше 0,5 заполнены электронами. Наоборот, все уровни, лежащие выше уровня Ферми, с вероятностью более 0,5 свободны от электронов. Распределение электронов по энергиям определяется не только вероятностью заполнения уровней, но и плотностью квантовых состояний в зоне:
dn(W) = N(W)F(W)d(W),
где dn – число электронов, приходящихся на энергетический интервал от Wдо W+ dW; N(W) – плотность разрешенных состояний в зоне, т.е. число состояний, приходящихся на единичный интервал энергии в единице объема.
Рисунок 1 – Распределение электронов в частично заполненной зоне (а) и функция вероятности заполнения электронами уровней (б): I – уровни, заполненные; II – интервал размывания; III – уровни, полностью свободные
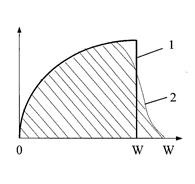
Распределение электронов по энергиям в металле можно представить параболической зависимостью, изображенной на рисунке 2. Электроны, расположенные в глубине от уровня Ферми, не могут обмениваться энергией с кристаллической решеткой, ибо для них все ближайшие энергетические состояния заняты. Общую концентрацию электронов в металле можно найти путем интегрирования по всем заполненным состояниям. При ОК это приводит к следующему результату:
Системы микрочастиц, поведение которых описывается статистикой Ферми – Дирака, называют вырожденными. В состоянии вырождения средняя энергия электронного газа практически не зависит от температуры. Электронный газ в металле остается вырожденным до тех пор, пока любой из электронов не сможет обмениваться энергией с кристаллической решеткой, а это возможно тогда, когда средняя энергия тепловых колебаний станет близкой к энергии Ферми. Для металлов температура снятия вырождения TF по порядку величины составляет 104 К, т.е. превышает не только температуру плавления, но и температуру испарения металлов. Вследствие вырождения в процессе электропроводности могут принимать участие не все свободные электроны, а только небольшая часть их, имеющая энергию, близкую к энергии Ферми. Только эти электроны способны изменять свои состояния под действием поля. Электрический ток, возникающий в металле под влиянием разности потенциалов, отражает изменения в распределении электронов по скоростям. В соответствии с квантовой статистикой это распределение является производным от распределения по энергиям (рисунок 2) и симметрично в отсутствие внешнего поля. Под действием электрического поля происходит рассеяние электронов под большими углами в процессе их упругих столкновений с узлами решетки. В результате этого возникает избыток быстрых электронов, движущихся против поля, и дефицит быстрых электронов с противоположным направлением скорости.
Рисунок 2– Распределение электронов по энергиям в металле: 1 – T=0 К; 2 – T¹0 К
Ускоряясь полем на длине свободного пробега, эти электроны приобретают добавочную скорость направленного движения:
где τF – время свободного пробега; VF – тепловая скорость быстрых электронов, обладающих энергией, близкой к энергии WF. Основная масса электронов не изменяет своего энергетического состояния при наложении поля. Однако в целом вся картина распределения скоростей смещается против поля (так как электроны имеют отрицательный заряд) на значение скорости дрейфа VF. Отдельные электроны неотличимы друг от друга. Поэтому, констатируя лишь конечный результат, можно считать, что под действием поля вся совокупность свободных электронов в металле (и быстрых и медленных) с концентрацией n приобретает добавочную скорость направленного движения, равную VF. С учетом этого обстоятельства, выражение для проводимости принимает вид:
При изменении температуры энергия Ферми WF изменяется незначительно, что является спецификой вырожденного состояния электронного газа. Например, при нагревании серебра от 0 до 1000 К энергия Ферми у него уменьшается лишь на 0,2%. Столь малые изменения в таком широком температурном диапазоне можно не учитывать. Это дает основание утверждать, что формула 8 справедлива при любой температуре. Концентрации свободных электронов в чистых металлах различаются незначительно. Температурное изменение n также очень мало. Поэтому проводимость определяется в основном средней длиной свободного пробега электронов, которая, в свою очередь, зависит от строения проводника, т.е. химической природы атомов и типа кристаллической решетки.
1.2 Особенности кристаллической структуры металлов и сплавов
В металле атомы расположены так, что образуют правильную кристаллическую решетку, что определяется минимальной энергией взаимодействия атомов. Наименьший объем кристалла, дающий представление об атомной структуре металла в любом объеме, называется элементарной кристаллической ячейкой. Они бывают кубическая объемноцентрированная (ОЦК), кубическая гранецентрированная (ГЦК) и гексагональная плотноупакованная (ГПУ). В гексагональной решетке атомы находятся в вершинах и центре шестигранных оснований призмы, а три атома в средней плоскости призмы. Расстояние между центрами ближайших атомов в элементарной решетке называют периодом решетки а. Обычно - а = 0,1 – 0,7нм. Плотность кристаллической решетки характеризуется координационным числом – числом атомов, находящихся на равном и наименьшем расстоянии от рассматриваемого атома. Так у ОЦК решетки координационное число 8, его обозначают К8, у ГЦК – К12. Для определения положения атомных плоскостей в кристаллических пространственных решетках пользуются индексами Миллера h, k, l. Они представляют собой три целых рациональных числа, являющихся величинами, обратными отрезкам осей, отсекаемых данной плоскостью на осях координат. Благодаря разной плотности атомов в различных плоскостях и направлениях решетки в металлах наблюдается анизотропия свойств. Технические металлы являются поликристаллами, т.е. состоят из большого числа анизотропных кристаллов, которые статически неупорядоченно ориентированы по отношению друг к другу. То есть поликристаллическое тело является псевдоизотропным. Такой изотропности не будет, если кристаллы имеют преимущественную ориентацию (текстуру) в каком – либо направлении; например, за счет значительной холодной деформации. В реальных кристаллах наблюдаются отклонения от регулярного расположения частиц, которые называются дефектами структуры. Дефекты классифицируют по геометрическим признакам: точечные, линейные, поверхностные. Точечные дефекты: – вакансии (дефекты Шоттки), – межузельные атомы (дефекты Френкеля). Вакансии возникают при переходе атомов из узла решетки на поверхность из-за испарения или в результате перехода в междоузлие. Тепловые вакансии характерны для поверхностного расположения атомов. С ростом температуры концентрация вакансий растет. При достижении температуры плавления Тпл такие вакансии достигнут 1% по отношению к числу атомов в кристалле. Быстрым охлаждением можно зафиксировать такие закалочные вакансии. Вакансии могут быть двойные, тройные. Наличие вакансий определяет диффузию. Дефекты Шоттки и Френкля влияют на проводимость, магнитные и другие свойства металлов. Линейные дефекты Чаще всего краевые и винтовые дислокации. Вокруг дислокации на протяжении нескольких межатомных расстояний возникают искажения решетки. Вектор Бюргера – критерий такого искажения – разность периметров контуров вокруг данного атома в плоскости удельной решетки и вокруг центра дислокации в реальной решетке. Поверхностные дефекты Эти дефекты малы только в одном измерении и представляют собой поверхности раздела между отдельными зернами или фазами. Сплав – это материал, полученный сплавлением двух и более компонентов. Если в твердом состоянии между компонентами нет химического взаимодействия, тогда по строению сплав – механическая смесь. Если составляющие сплав вещества вступают в химическое взаимодействие, то образуются химические соединения, например, двухкомпонентные AnBm. Если происходит растворение компонент, то имеем дело с твердым раствором (таблица 1). Таблица 1
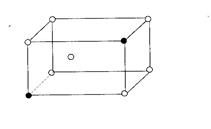
Твердые растворы – фазы, в которых один из компонентов сохраняет свою кристаллическую решетку, а атомы других компонентов располагаются в решетке первого компонента, изменяя ее размеры. Они бывают двух типов: – твердые растворы замещения (рисунок 3)
Рисунок 3- Схематичное изображение раствора замещения (· – замещенный атом)
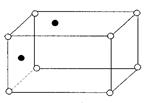
– твердые растворы внедрения (рисунок 4)
Рисунок 4- Схематичное изображение твердого раствора внедрения
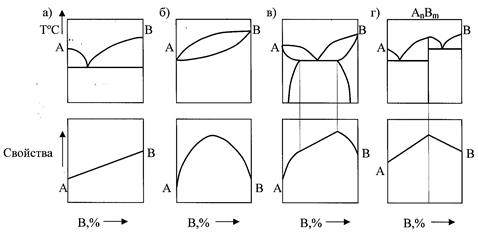
Твердые растворы на основе химических соединений образуются из компонентов с большими различиями в электронном строении, при этом сохраняется решетка соединения Аn Bm, но избыточное количество атомов, например В, растворяется, заменяя в решетке атомы А. Электрические, магнитные, механические свойства сплавов зависят от их фазового состава. Между типом диаграмм состояния и свойствами сплавов существует определенная взаимосвязь и впервые эту связь установил Н.С. Курнаков. В схематичном виде она представлена на рисунке 5. У сплавов, кристаллизующихся с образованием эвтектики во всем диапазоне концентраций, свойства изменяются по линейному закону в интервале между свойствами чистых компонентов (рисунок 5,а). У сплавов, кристаллизующихся с образованием непрерывных твердых растворов, свойства изменяются по кривой с максимум свойств, значительно отличающихся от свойств компонентов (рисунок 5,б). При образовании ограниченных твердых растворов свойства сплавов в области однофазных твердых растворов изменяются по нелинейному закону, а в двухфазной области – по линейному (рисунок 5,в). Если при кристаллизации сплавов образуется химическое соединение, то свойства сплавов при концентрации компонентов, соответствующей образованию этого химического соединения, достигают максимума (или минимума) на кривой изменения свойств с соответствующим изломом кривой. Точка перелома называется сингулярной точкой (рисунок 5,г). Твердые растворы могут обладать неограниченной растворимостью компонентов. Твердые растворы с неограниченной растворимостью образуются при условиях: – одинаковые типы кристаллических решеток у А и В; – различие в атомных размерах £8 – 15%; – близкое строение валентной оболочки электронов в атоме.
Рисунок 5
2 Температурная зависимость удельного сопротивления металлических проводников
В идеальном кристалле длина свободного пробега электронов равна бесконечности, а сопротивление электрическому току равно нулю. Подтверждением данного положения является тот факт, что сопротивление чистых отожженных металлов стремится к нулю, когда температура приближается к абсолютному нулю. Свойство электрона свободно перемещаться в идеальной кристаллической решетке не имеет аналога в классической механике. Рассеяние, приводящее к появлению сопротивления, возникает в тех случаях, когда в решетке имеются дефекты строения. Известно, что эффективное рассеяние волн происходит, когда размер рассеивающих центров (дефектов) превышает четверть длины волны. В металлах энергия электронов проводимости составляет 3 – 15 эВ. Этой энергии соответствует длина волны 3 – 7 В чистых металлах совершенной структуры единственной причиной, ограничивающей длину свободного пробега электронов, является тепловое колебание атомов в узлах кристаллической решетки. Электрическое сопротивление металла, обусловленное тепловым фактором, обозначим через ρтепл. Совершенно очевидно, что с ростом температуры увеличиваются амплитуды тепловых колебаний атомов и связанные с ними флуктуации периодического поля решетки. А это, в свою очередь, усиливает рассеяние электронов и вызывает возрастание удельного сопротивления. Чтобы качественно установить характер температурной зависимости удельного сопротивления, воспользуемся следующей упрощенной моделью. Интенсивность рассеяния прямо пропорциональна поперечному сечению сферического объема, который занимает колеблющийся атом, а площадь поперечного сечения пропорциональна квадрату амплитуды тепловых колебаний. Потенциальная энергия атома, отклоненного на ∆а от узла решетки, определяется выражением
где купр – коэффициент упругой связи, которая стремится вернуть атом в положение равновесия. Согласно классической статистике средняя энергия одномерного гармонического осциллятора (колеблющегося атома) равна кТ. На этом основании запишем следующее равенство:
Легко доказать, что длина свободного пробега электронов у N атомов обратно пропорциональна температуре:
Необходимо отметить, что полученное отношение не выполняется при низких температурах. Дело в том, что с понижением температуры могут уменьшаться не только амплитуды тепловых колебаний атомов, но и частоты колебаний. Поэтому в области низких температур рассеяние электронов тепловыми колебаниями узлов решетки становится неэффективным. Взаимодействие электрона с колеблющимся атомом лишь незначительно изменяет импульс электрона. В теории колебаний атомов решетки температуру оценивают относительно некоторой характеристической температуры, которую называют температурой Дебая ΘD. Температура Дебая определяет максимальную частоту тепловых колебаний, которые могут возбуждаться в кристалле:
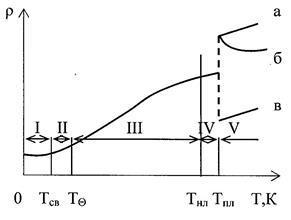
Эта температура зависит от сил связи между узлами кристаллической решетки и является важным параметром твердого тела. При T > Q D удельное сопротивление металлов изменяется линейно с температурой (рисунок 6, участок III). Как показывает эксперимент, линейная аппроксимация температурной зависимости rт (T) справедлива и до температур порядка (2/3)Q D, где ошибка не превышает 10%. Для большинства металлов характеристическая температура Дебая не превышает 400 – 450 К. Поэтому линейное приближение обычно справедливо при температурах от комнатной и выше. В низкотемпературной области (T<<Q D), где спад удельного сопротивления обусловлен постепенным исключением все новых и новых частот тепловых колебаний (фононов), теория предсказывает степенную зависимость rт~T5. В физике это соотношение известно как закон Блоха – Грюнайзена. Температурный интервал, в котором наблюдается резкая степенная зависимость rт(Т), обычно бывает довольно небольшим, причем экспериментальные значения показателя степени лежат в пределах от 4 до 6. В узкой области І, составляющей несколько кельвинов, у ряда металлов может наступить состояние сверхпроводимости (подробнее ниже) и на рисунке виден скачок удельного сопротивления при температуре Tсв. У чистых металлов совершенной структуры при стремлении температуры к ОК удельное сопротивление также стремится к 0 (пунктирная кривая), а длина свободного пробега устремляется в бесконечность. Даже при обычных температурах длина свободного пробега электронов в металлах в сотни раз превышает расстояние между атомами (таблица 2).
Рисунок 6 – Зависимость удельного сопротивления металлического проводника от температуры в широком диапазоне температур: а, б, в – варианты изменения удельного сопротивления у различных расплавленных металлов
Таблица 2 - Средняя длина свободного пробега электронов при 0°С для ряда металлов
В пределах переходной области II происходит быстрый рост удельного сопротивления ρ(T), где n может быть до 5 и постепенно убывает с ростом температуры ~ до 1 при T = Q D. Линейный участок (область III) в температурной зависимости r(T) у большинства металлов простирается до температур, близких к точке плавления. Исключение из этого правила составляют ферромагнитные металлы, в которых имеет место дополнительное рассеяние электронов на нарушениях спинового порядка. Вблизи точки плавления, т.е. в области IV, начало которой отмечено на рисунке 6 температурой Tнл, и в обычных металлах может наблюдаться некоторое отступление от линейной зависимости. При переходе из твердого состояния в жидкое у большинства металлов наблюдается увеличение удельного сопротивления приблизительно в 1,5 – 2 раза, хотя имеются и необычные случаи: у веществ со сложной кристаллической структурой, подобных висмуту и галлию, плавление сопровождается уменьшением r. Эксперимент выявляет следующую закономерность: если плавление металла сопровождается увеличением объема, то удельное сопротивление скачкообразно возрастает; у металлов с противоположным изменением объема происходит понижение ρ. При плавлении не происходит существенного изменения ни в числе свободных электронов, ни в характере их взаимодействия. Решающее влияние на изменение ρ оказывают процессы разупорядочения, нарушение дальнейшего порядка в расположении атомов. Аномалии, наблюдаемые в поведении некоторых металлов (Ga, Bi), могут быть объяснены увеличением модуля сжимаемости при плавлении этих веществ, что должно сопровождаться уменьшением амплитуды тепловых колебаний атомов. Относительное изменение удельного сопротивления при изменении температуры на один кельвин (градус) называют температурным коэффициентом удельного сопротивления:
Положительный знак αρ соответствует случаю, когда удельное сопротивление в окрестности данной точки возрастает при повышении температуры. Величина αρ также является функцией температуры. В области линейной зависимости ρ(Т) справедливо выражение:
где ρ0 и αρ – удельное сопротивление и температурный коэффициент удельного сопротивления, отнесенные к началу температурного диапазона, т.е. температуре T0; ρ-удельное сопротивление при температуре T. Связь между температурными коэффициентами удельного сопротивления и сопротивления такова:
где α0– температурный коэффициент сопротивления данного резистора; α1 – температурный коэффициент расширения материала резистивного элемента. У чистых металлов αρ>>α1, поэтому у них αρ≈ αR. Однако для термостабильных металлических сплавов такое приближение оказывается несправедливым.
3 Влияние примесей и других структурных дефектов на удельное сопротивление металлов
Как отмечалось, причинами рассеяния электронных волн в металле являются не только тепловые колебания узлов решетки, но и статические дефекты структуры, которые также нарушают периодичность потенциального поля кристалла. Рассеяние на статических дефектах структуры не зависит от температуры. Поэтому по мере приближения температуры к абсолютному нулю сопротивление реальных металлов стремится к некоторому постоянному значению, называемому остаточным сопротивлением (рисунок 6). Отсюда вытекает правило Маттиссена об аддитивности удельного сопротивления:
т.е. полное удельное сопротивление металла– это сумма удельного сопротивления, обусловленного рассеянием электронов на тепловых колебаниях узлов кристаллической решетки, и остаточного удельного сопротивления, обусловленного рассеянием электронов на статических дефектов структуры. Исключение из этого правила составляют сверхпроводящие металлы, в которых сопротивление исчезает ниже некоторой критической температуры. Наиболее существенный вклад в остаточное сопротивление вносит рассеяние на примесях, которые всегда присутствуют в реальном проводнике либо в виде загрязнения, либо в виде легирующего (т.е. преднамеренно вводимого) элемента. Следует заметить, что любая примесная добавка приводит к повышению r, даже если она обладает повышенной проводимостью по сравнению с основным металлом. Так, введение в медный проводник 0,01 ат. доли примеси серебра вызывает увеличение удельного сопротивления меди на 0,002мкОм ×м. Экспериментально установлено, что при малом содержании примесей удельное сопротивление возрастает пропорционально концентрации примесных атомов. Иллюстрацией правила Маттиссена является рисунок 7, из которого видно, что температурные зависимости удельного сопротивления чистой меди и ее сплавов с малым количеством (приблизительно до 4 ат. %) индия, сурьмы, олова, мышьяка взаимно параллельны.
Рисунок 7 – Температурные зависимости удельного сопротивления сплавов меди типа твердых растворов, иллюстрирующие правило Матиссена: 1 – чистая Cu; 2 – Cu – 1,03 ат.% In; 3 – Cu – 1,12 ат.% Nl
Различные примеси по-разному влияют на остаточное сопротивление металлических проводников. Эффективность примесного рассеяния определяется возмущающим потенциалом в решетке, значение которого тем выше, чем сильнее различаются валентности примесных атомов и металла – растворителя (основы). Для одновалентных металлов изменение остаточного сопротивления на 1 ат.% примеси ("примесный" коэффициент электросопротивления) подчиняется правилу Линде:
где a и b – константы, зависящие от природы металла и периода, который занимает в Периодической системе элементов примесный атом; D Z – разность валентностей металла – растворителя и примесного атома. Из формулы 15 следует, что влияние металлоидных примесей на снижение проводимости, сказывается сильнее, чем влияние примесей металлических элементов. Помимо примесей некоторый вклад в остаточное сопротивление, вносят собственные дефекты структуры – вакансии, атомы внедрения, дислокации, границы зерен. Концентрация точечных дефектов экспоненциально возрастает с температурой и может достигать высоких значений вблизи точки плавления. Кроме того, вакансии и междуузельные атомы легко возникают в материале при его облучении частицами высокой энергии, например, нейтронами из реактора или ионами из ускорителя. По измеренному значению сопротивления можно судить о степени радиационного повреждения решетки. Таким же образом можно проследить и за восстановлением (отжигом) облученного образца. Изменение остаточного сопротивления меди на 1 ат.% точечных дефектов составляет: в случае вакансий 0,010 – 0,015 мкОм × Ом; в случае атомов внедрения - 0,005 – 0,010 мкОм × Ом. Остаточное сопротивление представляет собой весьма чувствительную характеристику химической чистоты и структурного совершенства металлов. На практике при работе с металлами особо высокой чистоты для оценки содержания примесей измеряют отношение удельных сопротивлений при комнатной температуре и температуре жидкого гелия:
Чем чище металл, тем больше значение b. В наиболее чистых металлах (степень чистоты- 99,99999%), параметр b имеет значение порядка 105. Большое влияние на удельное сопротивление металлов и сплавов оказывают искажения, вызываемые напряженным состоянием. Однако степень этого влияния определяется характером напряжений. Например, при всестороннем сжатии у большинства металлов удельное сопротивление уменьшается. Это объясняется сближением атомов и уменьшением амплитуды тепловых колебаний решетки. Пластическая деформация и наклеп всегда повышают удельное сопротивление металлов и сплавов. Однако это повышение даже при значительном наклепе чистых металлов составляет единицы процентов. Термическая закалка приводит к повышению r, что связано с искажениями решетки, появлением внутренних напряжений. При рекристаллизации путем термической обработки (отжига) удельное сопротивление может быть снижено до первоначального значения, поскольку происходит "залечивание" дефектов и снятие внутренних напряжений. Специфика твердых растворов состоит в том, что rост может существенно (во много раз) превышать тепловую составляющую. Для многих двухкомпонентных сплавов изменение rост в зависимости от состава хорошо описывается параболической зависимостью вида
где C– константа, зависящая от природы сплава; xa и xв – атомные доли компонентов в сплаве. Соотношение 16 получило название закона Нордгейма. Из него следует, что в бинарных твердых растворах А – В остаточное сопротивление увеличивается как при добавлении атомов В к металлу А (твердый раствор a), так и при добавлении атомов А к металлу B (твердый раствор b), причем это изменение характеризуется симметричной кривой. В непрерывном ряду твердых растворов удельное сопротивление
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-06; просмотров: 54; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.119.163 (0.014 с.) |
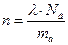 (1)
(1)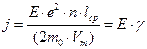 , (2)
, (2)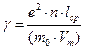 (3)
(3)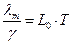 ,
, L0= (π2/3)·(R/e)2= 2,45·10-8 Вт·Ом/K2 – число Лоренца. Отклонения экспериментальных значений L0 от теоретических объясняется неупругими столкновениями электронов проводимости с колебаниями решетки.
L0= (π2/3)·(R/e)2= 2,45·10-8 Вт·Ом/K2 – число Лоренца. Отклонения экспериментальных значений L0 от теоретических объясняется неупругими столкновениями электронов проводимости с колебаниями решетки.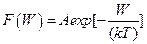 (4)
(4)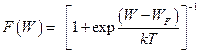 , (5)
, (5)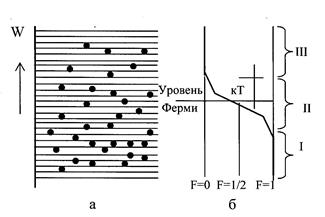
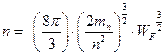 (6)
(6)
 , (7)
, (7)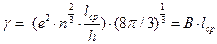 (8)
(8)
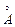 . Поэтому любые микронеоднородности структуры препятствуют распространению электронных волн, вызывают рост удельного сопротивления материала.
. Поэтому любые микронеоднородности структуры препятствуют распространению электронных волн, вызывают рост удельного сопротивления материала.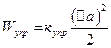 , (9)
, (9)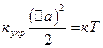
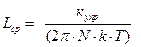 (10)
(10)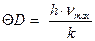
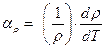 (11)
(11)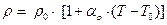 , (12)
, (12)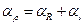 (13)
(13)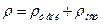 , (14)
, (14)
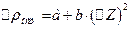 , (15)
, (15)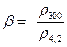
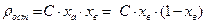 , (16)
, (16)


